基于DSP的混沌数字图像加密与硬件实现
2 基于Lorenz系统的数字图像加密
用驱动一响应同步对DSP中存储的数字图像进行混沌加密。考虑n维自治动力系统du/dt=f(u),把它分解为两个子系统v和w:dv/dt=g(v,w);dw/dt=g(v,w)。其中,v=(u1,u2,…,um),w=(um+1,um+2,…,un)按照加的形式复制1个子系统w’,即dw'/dt=g(v,w’),则构造了1个新的系统dv/dt=g(v,w),dw/dt=g(v,w),dw'/dt=g(v,w’),其中,系统(v,w)为驱动系统;(v,w’)为响应系统。当响应系统的条件李亚谱诺夫指数都为负值时,可实现混沌系统的同步。对于驱动一响应同步,并不是任何变量都可以用作驱动变量来实现混沌同步。显然,同步的要求是条件李氏指数均为负、或者可用李氏稳定性理论来证明其同步。同步的理论证明需要构造李氏函数,在一般情况下,李氏函数的构造并不容易。此外,条件李氏指数的计算也比较困难。为判断混沌是否同步,在工程实用方面,可通过相图来判断是否达到同步,即在同步情况下,同步相图为对角线,同步误差为0,从实际应用的角度,可通过仿真来确定用哪些变量驱动可同步,哪些不可同步。对于Lorenz系统,分别用X,Y,Z作为驱动变量来实现驱动-响应同步,通过Matlab仿真以后,发现用X,Y作为驱动变量时相图均如图4所示,达到同步时,同步相图为对角线,误差趋于0。而用Z作为驱动变量时,其相图如图5所示,同步相图不是对角线,误差不为0,不能实现同步。也就是说,对于Lorenz系统,用X,Y都可实现驱动-响应同步,用Z实现不了,在本文中用Y来驱动实现驱动-响应同步,其同步原理图,如图6所示。本文引用地址:https://www.eepw.com.cn/article/150847.htm
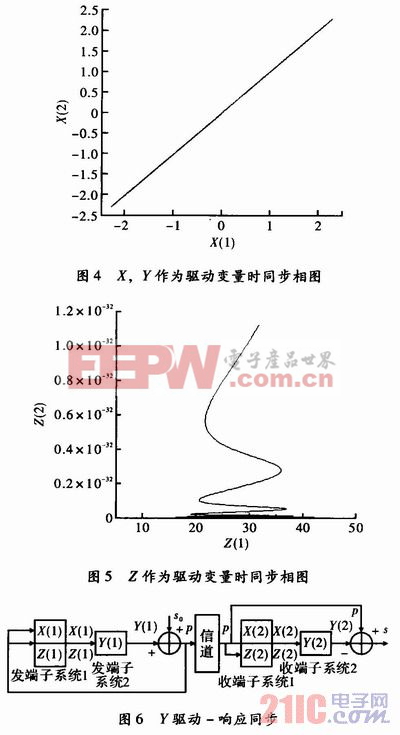
发送信号与接收信号均受同一信号P(t)驱动,在方程参数匹配的情况下,可实现严格的同步,这种严格的同步不受信号S0(t)幅度大小的影响。混沌信号与图像信号相叠加时,混沌信号要大于图像信号,但不能太大,否则将破坏系统的混沌状态。一般应满足,混沌信号与图像信号的比值在10~100之间。不同的混沌系统,比值的要求也不同。此外,在保密性要求较高时,一般取比值>100。









评论