​变分自编码器概述

摘要

变分自编码器（VAE）[1] 如今已经成为在复杂场景中进行推断（inference）的基本工具，同时它作为生成模型在生成连续型数据上也得到了广泛的关注和应用。本文简要介绍了变分推断的问题背景，接着介绍VAE的基本思想和原理，指出VAE是变分推断思想和神经网络结合的产物，并对它作简单的分析和理解。最后概述VAE的发展，包括在聚类任务上的应用，在生成任务上的改进，在无监督的解耦表征（disentangled representations）上的进展等等。

一、背景

近年来，随着机器学习的迅猛发展，许多先前未被考虑到的复杂场景都开始受到人们的关注。在这些场景中，进行推断和训练常常是困难且耗费巨大的。一方面，许多经典的算法在进行推断和训练时，常常有一些难以满足的条件或太强的限制，因此这些算法不能满足复杂场景的需求。另一方面，由于反向传播（Back propagation, BP）的发明和成熟，小批量梯度下降成为一种训练成本较低的高效方法。因此，一种能应用到复杂场景，且能够用小批量梯度下降训练的推断模型成为自然的发展需求，而VAE正是这种发展需求的产物。

由于VAE是变分推断和神经网络结合而来的成果，本节主要介绍VAE的思想背景：变分推断和ELBO。

1、推断问题 [2]

对于常见的数据如图片、视频、音频等，我们常常假设它们由一些更底层的变量生成，并且这些变量满足某些特定的分布，被称为潜变量（latent variable）。这些潜变量代表着数据的内在结构或者是某种抽象。设数据变量为x，潜变量为z，则这个普遍的假设即为以下生成模型：

其中P(z)是潜变量的分布，称为先验分布（prior）；而P(x丨z)则被假设为某种特定的分布如高斯分布。这些假设能使边际分布p(x)拟合任意光滑的数据分布q(x)，例如混合高斯分布就被证明为万能的分布拟合器。

推断问题关心的是：给定一个数据x (i)，并假设训练已经完成p(x)=q(x)，如何推断出后验分布？由贝叶斯公式我们可以得到：

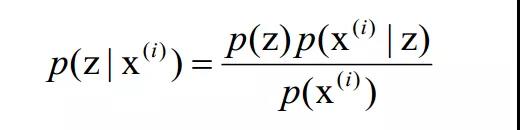
此处的困难在于分母部分是未知的。不幸的是，在大部分场景下，边际分布是难以处理的，因为的最优参数可能是高度复杂、未知或者没有解析表达式的。

2、变分推断和ELBO

为了解决推断问题，主要的方法有蒙特卡洛马尔可夫链（MCMC）和变分推断（Variational Inference, VI）。由于MCMC在训练中的每一步都需要大批量的数据，训练成本非常高。而变分推断则可以用BP算法和小批量梯度下降来训练，成本较低。VAE正是在变分推断上发展而来的。

变分推断是用一个分布q(z)来逼近后验分布，具体的做法是最小化以下KL散度：

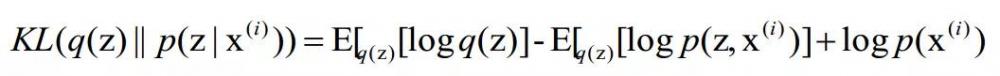
由于第三项是未知常数（称为log-evidence，在统计学上也称为log-似然函数），我们可以直接最大化负的前两项之和：

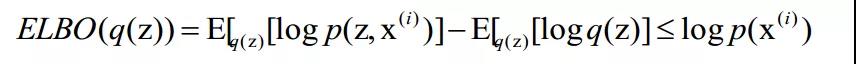
该式被称为ELBO（the Evidence Lower Bound），因为它是log-evidence的下界（由KL散度不小于0推出）。这个式子使得我们能够统一训练生成模型和推断模型，因为训练生成模型时，最大化似然函数等价于最大化ELBO；而训练推断模型时，最小化KL散度也等价于最大化ELBO。

然而，在高维连续的场景中，的数学期望仍然是难以处理的。为了发展出在复杂场景中具有通用性，能快速推断和训练的模型，VAE应运而生。VAE结合了ELBO的基本思想和神经网络，因而同时具有ELBO的良好性质和神经网络的强大拟合能力。值得注意的是，VAE在解决推断问题的同时，也将连续数据的生成问题一并解决了。

二、VAE

VAE继承了变分推断的思想：用一个分布去逼近后验分布。不同的是，VAE同时考虑所有数据的后验分布，对于每一个后验分布都用一个分布去逼近。即最小化以下KL散度：

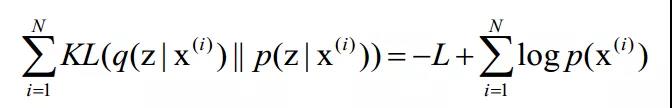
其中L是似然函数的下界，形式为：

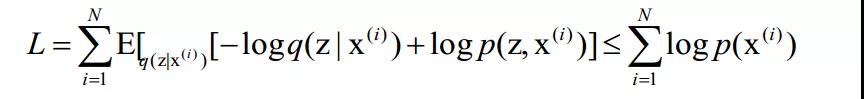
在VAE中，生成过程由一个神经网络参数化：

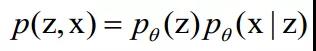
，该神经网络的参数记为θ。注意其中先验分布可以由网络生成，这大大提高了VAE的拟合能力。推断过程由另一个神经网络参数化

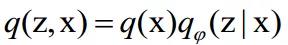
，该神经网络的参数记为，其中q(x)是数据分布。VAE的架构如下图所示：

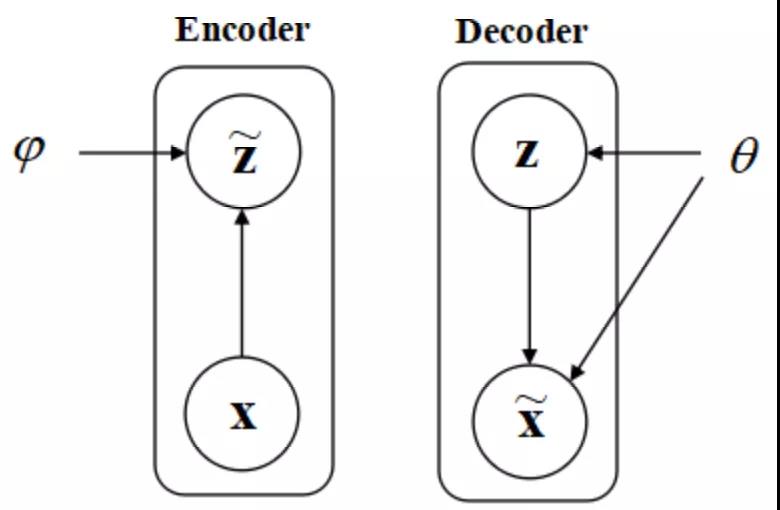
图 1 VAE的架构。编码器（Encoder）是推断模型，****（Decoder）是生成模型。箭头表示参数或者数据的输入输出。

由于VAE继承了ELBO的优点，使得生成模型和推断模型可以同时训练，即最大化下界就可以同时达到两个训练目的。这两个模型分别对应自编码器中的****和编码器，这就是VAE中AE的由来。

由于神经网络的引入，使得VAE可以将、和设为具有简单形式的分布如高斯分布（均值和协方差由神经网络生成），即可拟合非常复杂的数据分布q(x)。因为神经网络强大的拟合能力可以使得高斯分布的均值和协方差高度复杂，可以认为复杂性被蕴含在神经网络中。

1、训练VAE

首先，VAE显然能够用小批量梯度下降算法来训练，因为对于一个批量为M<<N的抽样，L仍然可以计算，并且各批次之间的训练并不相互影响。

其次要解决的是L的可计算性问题。L可以进一步改写为：

对于连续数据，VAE简单地假设

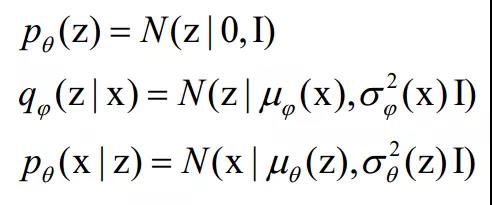
基于这些假设，L在训练中可以被高效计算。在(1)式中，第一项可以由解析表示，因而可以用BP算法来更新编码器。而第二项不可解析计算，但由于可由解析表示，因此这一项可以通过对进行采样来近似。但是采样操作不可梯度回传（BP）（因为一般来说，采样结果的无法表示为输入参数的函数），因此VAE提出用重参数化技巧（reparameter trick）来解决这个问题。具体地说，对于高斯分布而言，重参数化即是将从

中的采样结果表示为：

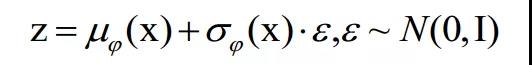
由于采样结果被表示为输入参数的函数，因此可以用BP算法来同时训练****和****。综上，VAE的训练问题得以解决，L的具体表达式为：

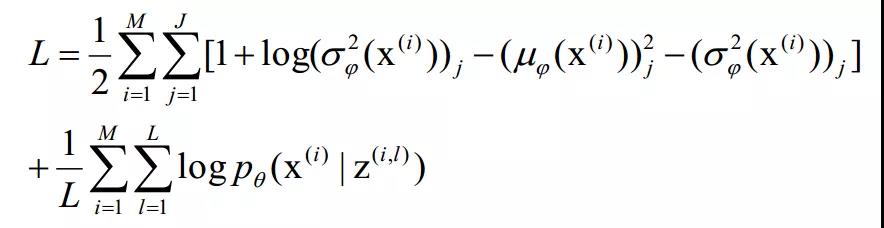
其中。

2、理解VAE

VAE成功地将神经网络应用到了推断问题中，同时也解决了连续数据的生成问题。在推断问题上，它具有训练快，成本低等优点；在生成问题上，它也具有训练快，高稳定性，高多样性，图片重建质量高等优点，但同时具有生成图片的清晰度低等缺点。理解这些优点的来源对于掌握VAE来说同样至关重要。

在(1)式中，第二项可理解为负重建误差（negative reconstruction error）。由于这一项的存在，使得VAE的重建效果较好，同时使得每一个数据的近似后验分布的支撑集趋向于分开。第一项则是负的KL散度，它使得每一个数据的近似后验分布都逼近先验分布，这导致它们的支撑集趋向于重叠（与第二项相反）。直觉上看，第二项的梯度在训练前期不为零，因而一般不会有梯度消失等稳定性问题，同时由于它倾向于将不同的数据混合在一起，因此一般不会有多样性缺失等问题。而生成图片的清晰度低的原因笔者尚不清楚。

以上讨论似乎揭示了L中的两项是对抗的，其实不然，因为L可以改写成编码器和****各自的联合分布的KL散度：

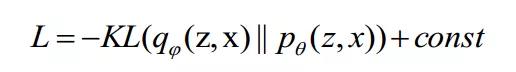
这说明VAE的优化目标是很合理的：编码器的边际分布q(z)逼近先验分布，****的边际分布p(x)逼近数据分布，同时保证数据的重建效果。

三、VAE的发展

如今VAE已经被应用到许多需要进行推断的场景中，比如在强化学习中用于推断对手的下一步动作上；作为生成模型VAE也同样得到广泛的应用，比如国内某公司宣称利用VAE开发出了快速的视频换脸工具。由于笔者比较关注VAE本身的发展，因此后文主要谈及VAE的发展，包括聚类、图片生成、无监督的解耦表征学习（disentangled representation learning）三个方面。由于VAE还有许多其他方面的发展，不能一一概述，读者可自行学习。

1、聚类

将VAE用于聚类的核心思想在于将（GMM）聚类引入到潜空间（latent space）。一般地，假设潜变量服从离散型的混合高斯分布（该先验分布由神经网络生成，是可变而非固定的，这是VAE的自然发展），并相应地解决下界函数L的可计算性问题即可实现这一思想，主要有GMVAE [3] 和VaDE [4] 等。

2、图片生成

VAE在图片生成任务上的巨大进展主要是VQ-VAE [5] 系列方法的诞生，其生成效果能够媲美BigGAN。VQ-VAE的主要思想是对潜变量采用自回归过程来训练和采样，从而得到结构化的全局语义概率分布。具体地说，自回归是很强的生成模型但是计算量太大，因此对先将高维的图片压缩为低维的潜变量，再对潜变量进行自回归就能大大提高生成效果。同时由于VAE中潜变量的每一个维度都对应一个结构化的全局语义信息，因此这种方法并没有太多的冗余。

3、无监督的解耦表征学习

解耦表征学习的目的是学到的表征（编码）中每一个维度都能对应数据中独立的属性。这方面近来有许多无监督的工作，包括FactorVAE [6]，TC-VAE [7] 等。这些工作的主要方法可以归纳为惩罚以下KL散度：

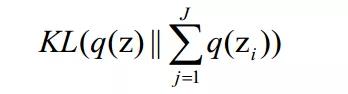
不幸的是，Francesco等人指出 [8] 这种方法缺乏理论基础，并且通过实验证明这些模型的效果并不能超出VAE调参的效果。因此这个领域目前仍处于迷雾中。

四、总结

VAE是变分推断的自然发展，它结合了ELBO和神经网络的优势，解决了通用场景下的推断问题，同时也解决了连续数据的生成问题。它具有很多优势，包括训练快、稳定等，从而在理论模型和工业界上都有广泛的应用。它的缺点也有待进一步的研究，包括普通VAE的生成图片不清晰等问题。它在离散数据上的应用、非监督的解耦表征学习都是热点，对它更深入的理解也是仍需解决的问题。

参考文献：

[1] Kingma D P, Welling M. Auto-Encoding Variational Bayes[J]. international conference on learning representations, 2014.

[2] Blei D M, Kucukelbir A, Mcauliffe J, et al. Variational Inference: A Review for Statisticians[J]. Journal of the American Statistical Association, 2017, 112(518): 859-877.

[3] Dilokthanakul N, Mediano P A, Garnelo M, et al. Deep Unsupervised Clustering with Gaussian Mixture Variational Autoencoders[J]. arXiv: Learning, 2017.

[4] Zhuxi Jiang, Yin Zheng, Huachun Tan, et al. Variational Deep Embedding: A Generative Approach to Clustering. arViv: Learning, 2016.

[5] Den Oord A V, Vinyals O, Kavukcuoglu K, et al. Neural Discrete Representation Learning[J]. neural information processing systems, 2017: 6306-6315.

[6] Kim D H, Mnih A. Disentangling by Factorising[J]. international conference on machine learning, 2018: 2649-2658.

[7] Chen T Q, Li X, Grosse R B, et al. Isolating Sources of Disentanglement in Variational Autoencoders[J]. neural information processing systems, 2018: 2610-2620.

[8] Locatello F, Bauer S, Lucic M, et al. Challenging Common Assumptions in the Unsupervised Learning of Disentangled Representations[J]. international conference on machine learning, 2019.