MEMS固态风速风向传感器的设计与制作

　　1 引言

　　风速及风向的测量是气象观测中重要的一环。风速风向可以基于流体力学原理、热学原理、声学原理和仿生学原理来测量。热式测风仪基于风对热体的对流作用来测量风速和风向，其存在一个精密的热源，通过把两对相对的热源与热电偶正交放置测量风向。超声测风仪可以同时进行超声波的发射和接收，基于多普勒效应测量风速，用三个或者四个探头根据三角关系测量风向信息。基于MEMS技术传感器有体积小、重量轻及成本低的特点，基于MEMS技术的风速和风向测量传感器受到了研究者的重视。

　　本文介绍了基于MEMS的固态风速风向传感器的设计原理及软件模拟结果，并依据理论与模拟结果设计了工艺流程，对设计的悬梁式测风传感器进行了测量。

　　2 传感器原理

　　2.1 硅薄膜式传感器原理

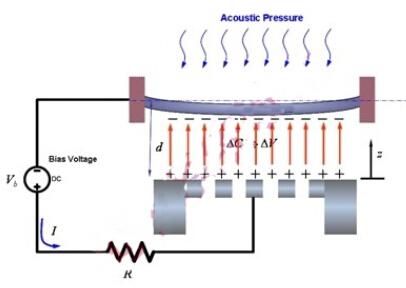
　　硅薄膜式测风传感器的设计示意图如图1所示。薄膜式风速风向传感器主要是利用风吹薄膜对薄膜产生风压，风压导致薄膜形变，薄膜上的应变电阻就会感应到薄膜的形变。通过测量应变电阻的变化即可解算出风速大小。设定测量时风正面吹向薄膜如图2所示。

　　图2中：υ1表示风的平均流速;p1表示风流的压力;p2表示薄膜所受的压力，应用流体力学中理想伯努力方程如式(1)。其中p为空气的密度，化简后可以得出薄膜承受绝对压强p的变化与风速的关系如式(2)，即

　　设W(x，y)是薄膜弯曲的挠度函数。由式(2)可以得出0～30 m/s风的压强为0～580.5 Pa。在此范围之内薄膜的挠度远小于薄膜的厚度，故挠度可以近似计算为

　　W(x，y)=hf(p)cos2(πx/L)cos2(πy/L)(3)

　　其中坐标系是平面直角坐标系，其原点是正方形薄膜中心，坐标轴平行于薄膜的边。其中h和L分别是薄膜的厚度和边长。f(p)是一个关于薄膜绝对压强的函数。f(p)由方程(4)决定，即

　　p是作用在膜上的绝对压强;E和υ分别为薄膜材料的杨氏模量和泊松比。材料的形变定义为单位长度材料的变化。设ε(x，y)是薄膜的应变函数，可以用式(5)来计算，则

　　薄膜上的应变电阻的形变与其所在的位置有关。定义h′为应变电阻的高度;W为应变电阻的宽度;x0，y0是应变电阻的起始位置，则可以得到应变电阻的总的形变，如式(6)。应变电阻的电阻归一化变化表达式为

　　由式(2)可知p与速度υ的平方成正比，故可以得出电阻阻值的相对变化与风速是二次关系。风速信号解调出来后，通过正交封装来解调风向信号。南北方向的传感器测出南北方向的速度υns，东西方向的传感器测出东西方向的速度υwe，通过正交关系式(9)和式(10)最终得出速度和风向值，即

　　2.2 硅悬梁式传感器原理

　　硅悬梁式测风传感器的设计示意图如图3。悬梁式风速风向传感器主要是利用风吹悬梁对悬梁产生力矩导致悬梁弯曲，悬梁上的应变电阻就会感应到薄膜的应变。通过测量应变电阻的变化即可解算出风速大小。测量时风流平均速度为u(y)。根据流体力学绕流阻力计算公式(11)。其中CD是绕流阻力因素取决于材料的形状结构，ω是面向风速的悬梁宽度，ρ是空气密度。通过公式(12)得到风对悬梁力矩的作用，其中l是悬梁的长度，y为悬梁长度方向，即

　　悬梁的应变通过式(13)来计算，E是杨氏模量，I是惯性矩。惯性矩计算公式是式(14)，t是悬梁的厚度，ω是悬梁的宽度，则

　　应变电阻的阻值变化可用式(7)计算，即可得电阻变化的归一化的表达式为

　　并可以得出电阻阻值的相对变化与风速是二次关系。和薄膜式传感器一样，可以通过正交二次集成的方法解算山风向的信息。

　　3 传感器ANSYS CFD模拟

　　3.1 硅薄膜式传感器模拟

　　为了方便软件模拟，简化了所设计传感器的模型。薄膜的厚度取10μm，2000 μm×2000μm的正方形，空腔的厚度取330μm。图4为带有薄膜形变的ANSYS模型。薄膜的模型用Solid45，流体模型应用FLUID142，风速从0～30 m/s间隔变化。通过模拟得到了薄膜最大形变、最大应力与风速的关系曲线，见图5。分析模拟所得的数据，可知薄膜挠度和剪切力都与风速成二次关系，与薄膜式传感器的理论分析相一致。

　　3.2 硅悬梁式传感器模拟

　　所设计的悬梁式传感器的模型为悬梁的厚度取10 μm，长度取1500 μm。采用二维ANSYS模拟。悬梁的模型用Solid42，流体模型应用FLUID141，风速从0～30 m/s间隔变化。图6为带有悬梁形变的ANSYS模型。通过模拟得到了薄膜最大形变、最大应力与风速的关系曲线，见图7。

　　把模拟所得的数据进行分析，可知悬梁挠度、剪图7切力都与风速成二次关系，与悬梁式传感器理论分析相一致。

　　4 传感器工艺流程、封装及制作

　　4.1 传感器工艺流程设计

　　两种传感器拟采用基于MEMS的体硅工艺，应用正背面异向湿法刻蚀和背面深刻蚀形成薄膜或悬梁。薄膜设计为10μm厚，200 μm×2000 μm的正方形;悬梁设计为10μm厚，1500 μm长，500 μm宽。采用双面抛光n型(76 mm)100硅片厚度350 μm。硅片清洗后，用热氧化工艺制作一层氧化硅，再用LPCVD工艺制作一层氮化硅;之后溅射Pt电极，采用lift-off工艺去掉不需要的Pt金属。完成以上步骤后，薄膜式传感器直接在背面腐蚀形成薄膜，完成传感器的制作;悬梁式传感器需要先在正面腐蚀出10μm的深坑，后在背面先湿法腐蚀5 h深度达到200μm，再深刻蚀直到出现图形。其过程如图8。

　　4.2 传感器封装设计

　　测风传感器通过正交的封装测量风向信息。正交封装示意图如图9所示。

　　通过用风向信息解算公式(9)和(10)，即可得出风向信息。

　　4.3 传感器制作

　　依据所设计的原理及工艺流程，首先制作了悬梁式测风传感器如图10所示。传感器为双悬梁结构，通过惠斯通电桥输出传感器测量信号，其测试图如图11所示。

　　传感器经小型风洞测试后得出，其一致性很好。转动传感器，其输出信号有变化，这说明可以通过正交的方法计算出风向。

　　5 结 论

　　本论文推算了两种风速风向传感器的理论，并进行了基于理论的软件模拟，设计了传感器工艺制作流程和封装，对按照本文中所设计的理论与原理制作的硅悬梁式传感器进行了实际测量。传感器可以很好地感应风速的变化，根据输出电压随着传感器旋转的变化，可以计算出风向。