Δ-Σ转换器的信噪比如何不同
当我还是孩子的时候,父母送给我一个内径为1的箱子。我非常的兴奋!为了保护这个海龟,我准备把它放到我的货车上。车上有个狭槽可以嵌入方形,三角形和圆形的销子。妈妈看到我拿走一个锤子,就知道肯定不会有好事。她对我说:“你不能将一个方形的销子放进一个圆形的孔中”。
这件教训也同样适用于下面的Δ-Σ调节器和ADC中——一个从1930年起被提出的基本概念。转换器的拓扑结构与其他拓扑的结构有一点不同。然而,许多工程师仍努力使转换器适应标准ADC方形孔。
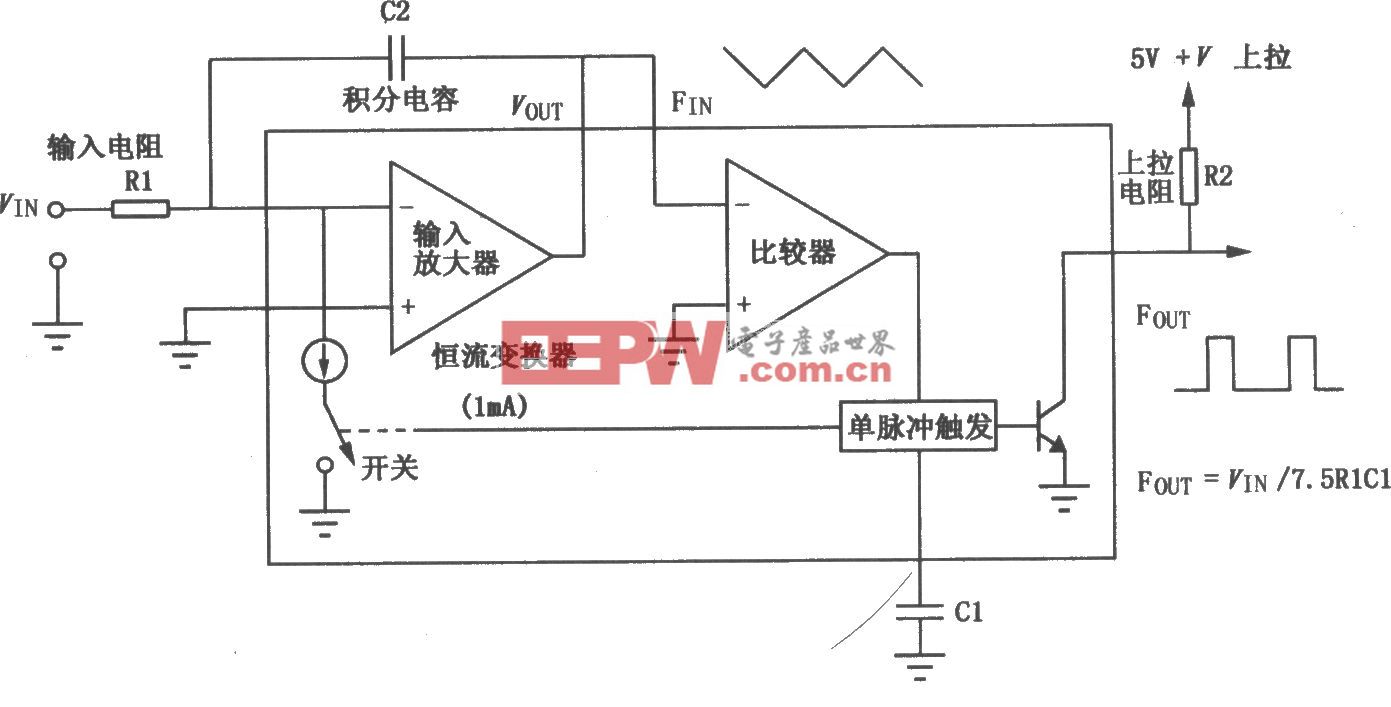
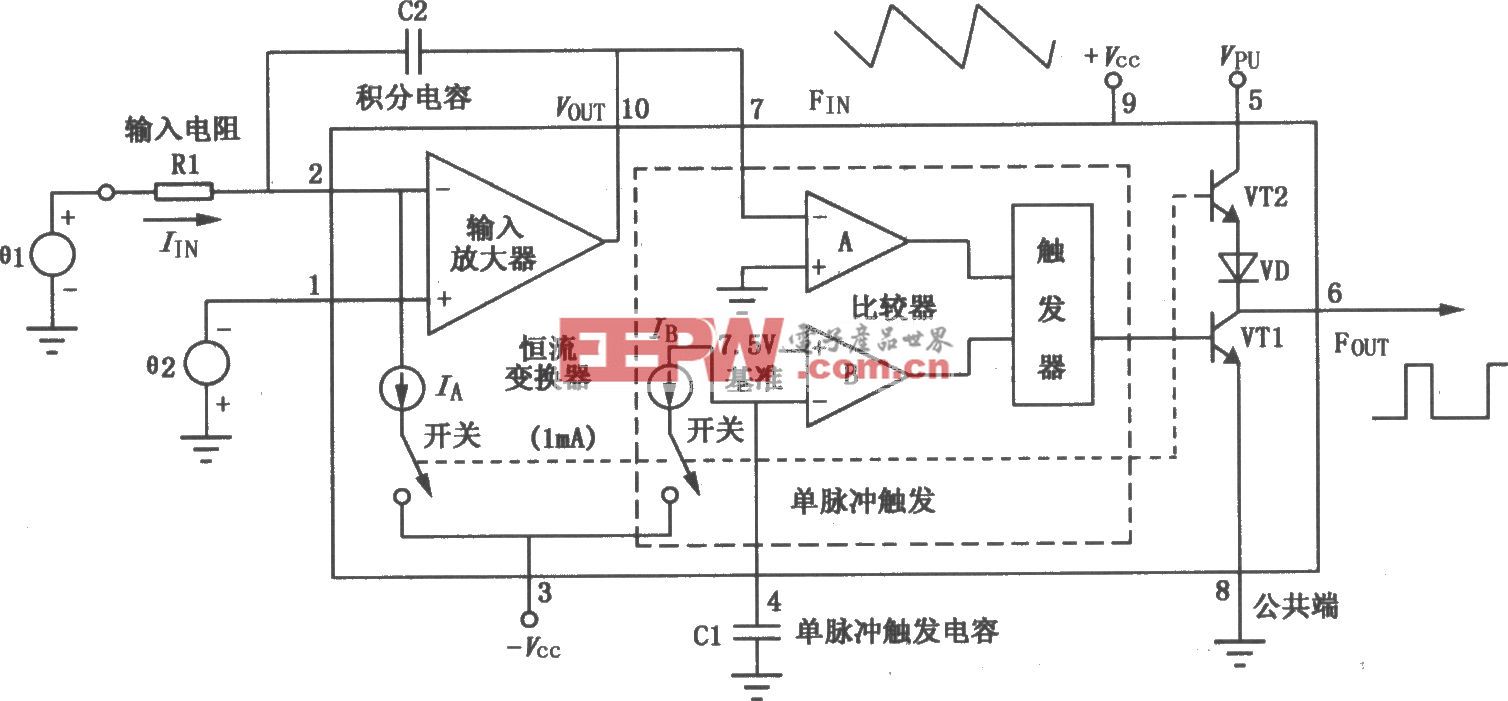
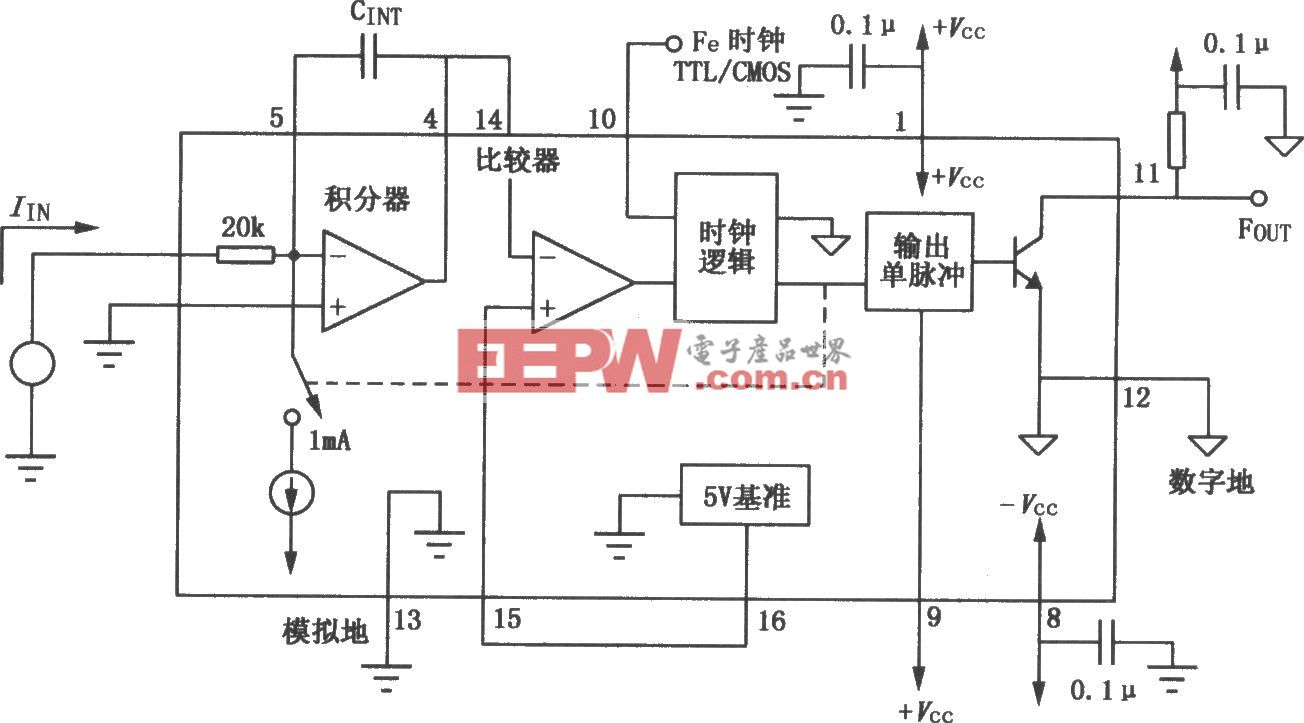
Δ-Σ转换器的性能远超一般简单的模数转换器。它有过采样结构、调节器和数字滤波器。过采样结构在较宽的频率范围内扩展噪声功率。调节器形成低频噪声或将其推到更高频率。数字滤波器可以平滑噪声信号并将其从高频信号中消除。完美的逐次逼近记录寄存器和传递途径信噪比为6.02N+1.76(参考文献1),其中N为转换器位数。Δ-Σ转换器的信噪比是6.02(N+NINC)+1.76,其中,N是调节器位数,NINC是增加的分辨率是:

在这个公式中,M是调节器阶数,K是转换过程中的过采样速率。
理想的带一阶调节器的Δ-Σ转换器信噪比是6.02N+1.76–5.17 +30log10OSR,其中OSR为过采样速率,N为调制器位数而不是转换器的位数(如图1)。

这些理想公式假定ADC和DAC的噪声和偏移误差为线性的,通常一阶设备是理想的,数字滤波器也会有一个理想的砖墙型反应。事实上,Δ-Σ转换器并不想我们希望的那么理想。
由这些理想的理论,最好的方法仍是依靠转换器性能的基准数据。这些数据给你转换器性能的现实看法。在这个基础上,通过获取上百次直流输入信号的采样,来测量转换器的均方根噪声。在这种情形中,描述任意ADC信噪比的公式是20log10(VRMS-FS/VRMS-NOISE)。
参考文献:
1.Baker, Bonnie, “Where did all the bits go?” EDN, June 7, 2007, pg 36.
2.Baker, RJ, CMOS Mixed-Signal Circuit Design, Wiley-IEEE Press, 2002.
3.Norsworthy, Steven R, Richard Schreier, and Gabor C Temes, Delta-Sigma Converters: Theory, Design, and Simulation, Wiley-IEEE Press, 1996.
英文原文:
How the SNRs of delta-sigma converters differ
This converter topology is a bit different from other topologies; however, many engineers still strive to fit this round peg of a converter into the standard ADC square hole.
By Bonnie Baker -- EDN, 8/2/2007
When I was a child, my parents bought me a 1-in.-diameter box turtle. I was so excited! To protect the turtle, I was going to put it in my block wagon. This wagon had slots to insert square, triangular, and round pegs. When my mom saw me grab a hammer, she knew it wouldn’t be a pretty picture. “You can’t fit a square peg—or a turtle—into a round hole,” she told me.
That lesson also applies to the basic concept underlying delta-sigma modulators and ADCs—a concept that has been around since the 1930s. This converter topology is a bit different from other topologies; however, many engineers still strive to fit this converter into the standard ADC square hole.
Delta-sigma converters go beyond performing a simple analog-to-digital conversion. They have an oversampling mechanism, a modulator, and a digital filter. The oversampling mechanism spreads the noise power across a wider frequency range. The modulator shapes the low-frequency noise or pushes it out to higher frequencies. The digital filter averages the noise and eliminates it in the higher frequencies. The id eal successive-approximation-register and pipeline SNR (signal-to-noise ratio) is 6.02N+1.76 (Reference 1), where N is the number of converter bits. The delta-sigma-converter SNR is 6.02(N+NINC)+1.76, where N is the number of modulator bits and NINC, the increase in resolution, is:
In this formula, M is the order of the modulator, and K is the oversampling ratio during the conversion.
Ideally, the delta-sigma-converter SNR, with a first order modulator, is 6.02N+1.76–5.17+30log10OSR where OSR is the oversampling rate and N is the number of modulator bits—not converter bits (Figure 1).
These ideal formulas assume that the linearity, noise, and offset errors of the ADC and DAC—usually, 1-bit devices—are ideal and that the digital filter has an ideal brick-wall response. Actual delta-sigma converters are not as ideal as you would hope.
With these theories of the ideal, the best approach is still to rely on bench data for your converter performance. This data gives you a realistic view of the converter’s capabilities. On the bench, you can measure your converter’s rms noise by acquiring a few hundred samples of a dc-input signal. In this circumstance, the formula that describes any ADC SNR is 20log10(VRMS-FS/VRMS-NOISE).






评论