基于RNS和SVM的断路器故障诊断研究
摘要:针对高压断路器故障样本难以获取等问题,在研究了其机械特性的基础上,本文提出了一种基于实数阴性选择法(RNS)和支持向量机(SVM)的两级分类器诊断方法。建立分类器的数学模型。通过实数阴性选择算法产生检测器,进行第一次分类,对不属于检测器的数据导入二次分类器,进行二级分类。实验表明,基于实数阴性算法和支持向量机算法相结合的断路器故障诊断算法,对断路器的多种故障都能够有效地分类,提高了断路器故障诊断的准确率和速度。
本文引用地址:https://www.eepw.com.cn/article/201610/306580.htm高压断路器是电力系统的重要设备之一,是电网运行中正常状态下切换电路和故障状态下断开电路的主要设备,在电网中能起到保护和控制作用。其运行状态的安全与否直接关系到整个电力系统的安全性。因此,随时检测断路器状态,及早发现并排除可能存在的故障,是保障供电系统可靠性的重要手段之一。
近年来,出现了许多新的故障诊断方法,如神经网络、故障树、支持向量机、灰色理论、专家系统、遗传算法等。在断路器故障诊断方面,这些方法存在部分缺陷,例如神经网络会出现局部极小值、敛速度慢、欠学习与过学习以及训练网络时需要大量样本等不足。所以基于以上方法融合的智能诊断方法可发挥各自优势,克服各自的缺陷。针对高压断路器故障样本难以获取的问题,文中在研究了以上种方法的基础上,提出了基于实数阴性选择法和支持向量机的复合诊断方法。
1 实数阴性选择法
阴性选择法(RNS)是人工免疫系统的算法中的一种算法,免疫系统是人类和脊椎动物体必备的防御系统,人工免疫系统,是基于是基于免疫系统机制和理论免疫学而发展的各种人工范例的统称,其主要过程是抽取免疫机制、设计免疫模型或算法、实验验证或计算机仿真(解决问题)。
阴性选择法是Forrest的研究小组在于免疫系统的专家合作研究中首次提出的,算法模拟了免疫细胞的成熟过程,形成检测器模拟成熟的免疫细胞。主要的过程分为两个阶段:耐受和检测。耐受阶段主要通过现有样本产生成熟的检测器,建立非己;检测阶段,检测器对未知的采样样本进行检测,以发现变化。通过随机产生检测器,并删除那些能检测出自己的检测器,以便生成的检测器集有更好的空间覆盖率能,更好的检测出非己。
实数阴性选择法的组成包括数据空间表示、检测器的表示、匹配规则、检测器产生清除机制,其中最重要的检测器的生成。
实数阴性选择算法可以阐述为:把自己/非已空间作为Rn的一个子集,归一化到空间[0,1]n。检测器由一个n维向量和一个实数构成,用n维向量表示检测器中心,实数表示列应的半径。因此,检测器可以看作Rn空间内的一个超球。匹配规则由检测器与自己间的欧氏(Euclidean)距离和检测半径组成。将已知样本S(表示为n维向量的点)作为算法的输入,通过算法产生检测器D让它覆盖非己空间。检测器具有只与非己空间匹配、不与自己空间匹配的特性。向量检测器具有与自己向量相同的维数,但其分布在非己空间内,向量检测器D需满足以下不等式:
E(D,S)>r (1)
其中,E(·)为D与S的欧氏距离,S为自己空间的任意样本向量,r为阈值。
2 支持向量机
支持向量机是一种监督式学习方法,是Cortes和Vapnik于1995年提出的,他在解决小样本,非线性,高维模式识别中表现出许多特有的优势,并能够推广应用到函数拟合和其他机器学习问题中。
支持向量机是建立在统计学习理论和结构风险最小原理基础上的,根据有限的样本信息在模型的复杂性学和学习能力之间寻求最佳折衷,以期获得最好的泛华能力。
支持向量机主要针对样本的二分类问题,在样本数量小、非线性的情况下,可以很好的样本分类的效果,由于支持向量机对样本的依赖程度较低,相比神经网络,能更好的反应现场的状况,支持向量机主要是构建一个超平面。

根据以上公式,求出支持向量,阈值b,并求出最优分类超平面。
3 断路器故障诊断实验
断路器的机械特性主要通过分合闸信号来体现,DSP采集传感器的信号,通过小波去噪和小波重构等方法获取分合闸信号的关键参数:I1,I2,I3,t1,t2,t3,t4,t5。如图1所示:其中t0~t1为铁芯的启动时间,t1时刻铁芯开始运动,t1~t2铁芯运动,t2时刻铁芯碰到机械负载,达到电流谷底。t2~t3铁芯停止运动,t3~t4为上一阶段的延续,t4~t5为电流开断阶段,此时辅助开关分断,在辅助开关处产生电弧,迫使电压升高,电流快速下降。I1,I2,I3,分别反映了电源电压、线圈电阻,电磁铁芯运动速度。
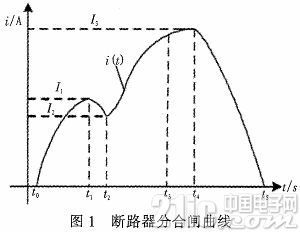
当分合闸信号出现异常时,表示断路器可能出现了故障。常见的故障有:电源过低(GD)、合闸铁心有卡涩(HKS)、操作机构有卡涩(CKS)、合闸铁芯空行程太大(TD)、辅助开关接触不良(FK)。
3.1 诊断模型建立
模型的建立有两种模式,第一种为:通过已知样本获取检测器,将已知的多类故障样本、已知正常样本、检测器作为支持向量机的输入,建立支持向量机模型。为了实现对未知故障有较高的覆盖率,检测器的个数在试验中达到1 000个,导致在生成支持向量机模型和未知样本做测试时会花费大量的时间,不利于故障的快速诊断。第二种为:第一阶段,将未知样本代入检测器,判断是自己还是非己,如果是非己,则代入有已知样本构建的支持向量机模型。经过试验论证,这样会大大加快诊断的速度,并且能够保证诊断的精度。
如图2所示,首先通过已知样本,其中包括正常样本和故障样本,建立实数阴性选择法的模仿,得到检测器。将待检测的样本代入一级分类诊断模型,计算其亲和力,判断是否为自己,如果是非己则将其代入二级分类诊断模型,对故障进行具体分类。
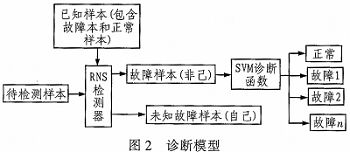
3.2 一级分类模型建立
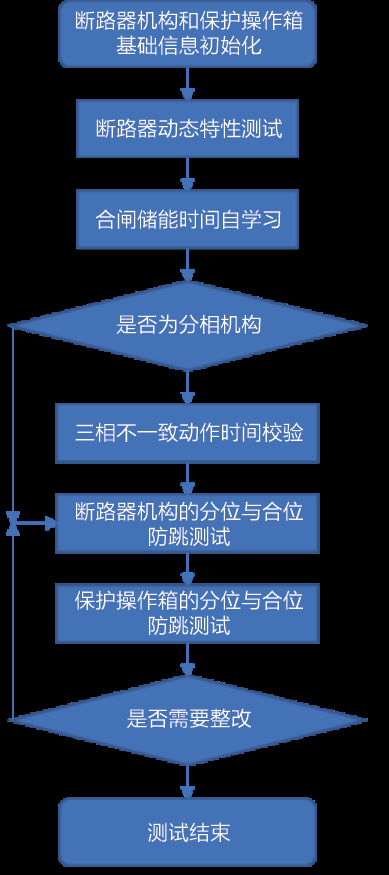
1)检测器成熟阶段。如图3所示:输入参数,S-自体样本,Nmax-最大检测器数,rs-自体半径,rd-检测半径。将自体样本用公式归一化到n维空间[0,1]n
![]()
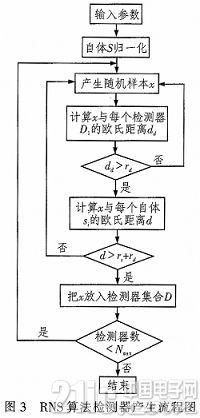
其中,S(i)为自体样本S矩阵的第i列,min[S(i)]为S(i)中所有元素的最小元素,max[S(i)]为S(i)中所有元素的最大元素,B’=[1,1,…,1]1×n,n为样本的维数,s(i)为归一化后的自体样本s矩阵的第i列。再从[0,1]n空间中随机产生样本x,计算x与检测器集合D中的每个检测器Di的欧氏距离dd和x与每个自体样本si的欧氏距离d。Di,Si和x分别为n维向量,是空间[0,1]n中的一个点。
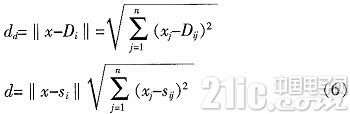
最后,满足条件dd>rd且d>rs+rd的x为非己,将其放入检测器集合D中直到检测器个数满足要求。条件dd>rd用来保证x与检测器集合D中已有的每个检测器的欧氏距离大于rd,
防止检测器过度聚集,使其更均匀的覆盖非己空间;条件d>rs+rd用来保证检测器落在非己空间。
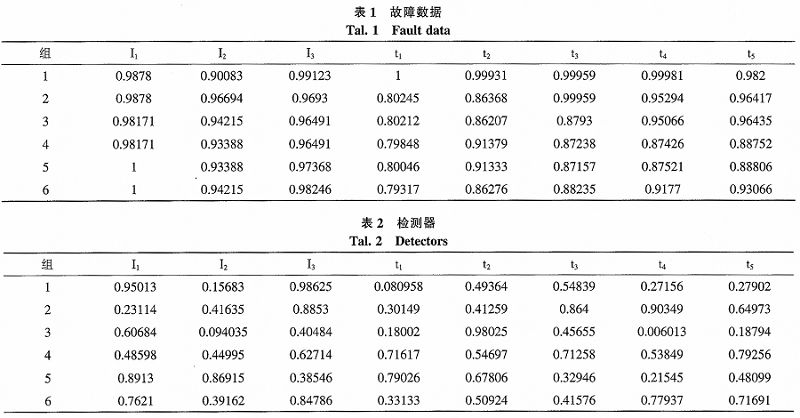
根据上述所述,断路器归一化后的部分故障参数如表1所示,通过随机产生检测器,设定rs=O.05、rd=0.1,按照上述的规则生成检测器,部分检测器如表2所示。
2)诊断阶段。将未知样本带入训练好的检测器,判断自己还是非己,如果是非己,将数据导入二级故障分类模型,完成系统的故障诊断任务。
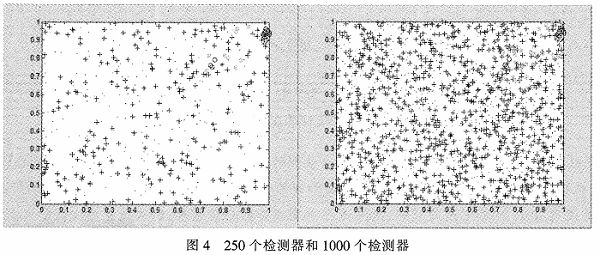
取样本和检测器前二维作图,检验结果如图4所示,左边图为250个检测器,右边图为1 000个检测器,图中“+”为检测器,“o”为已知样本,“*’为待检测样本。从图中可以看出当检测器达到1 000个的时候,检测器基本上覆盖了整个区域。经过试验论证,1 000个检测器与250个检测器相比,故障诊断的正确率提高了23%,整体正确率达到了92%,并且在诊断时间上没有增到多少,符合故障诊断的要求。
3.3 二级分类模型建立
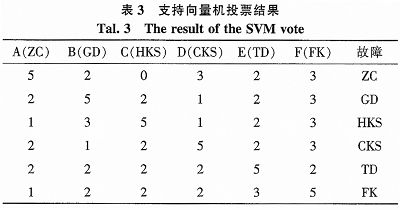
已知样本中有正常样本和具体的故障样本,将正常样本和故障样本(5类)作为支持向量机的输入。支持向量机是用来解决二分类问题的,在解决多分类问题的时候,需要加以改进,这里我们采用1对1的训练方法(OVO),将训练样本分成A、B、C、D、E、F六类,建立15个SVM,求解出15个判断函数组成的诊断模型。将不符合检测器的数据作为诊断模型的输入,获得每个判断函数的判断输出,采用投票的方法,确定最终的诊断结果。
如表3所示,将6组不符合检测器的数据带入诊断模型可以很快的得出具体的故障类型,得出的结果与真实故障类型比较,正确率为100%,诊断模型在速率和准确度方面都有很大的改进。
4 结论
针对断路器故障数据难以获取的问题,在深入研究了实数阴性选择法和支持向量机的机理后,本文建立了基于实数阴性选择法和支持向量机的二级分类器模型。将已知样本作为检测器的输入,产生检测器集。将检测集和已知样本建立第一级分类器,通过此算法能够很好的覆盖非己空间。利用已知样本建立二级分类器,用来具体区分故障类型。在故障样本难以获取的情况下,两种算法的结合,大大发挥了其各自的优势,提高了断路器故障诊断的准确率和速度。




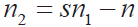

评论