基于SOPC的高精度超声波雷达测距系统设计

　　上述经卡尔曼滤波算法优化后的数据会送到LCD液晶屏显示，一部分数据显示为实时数值数据，另一部分则先存储，然后在LCD液晶屏的指定区域显示为实时波形数据。

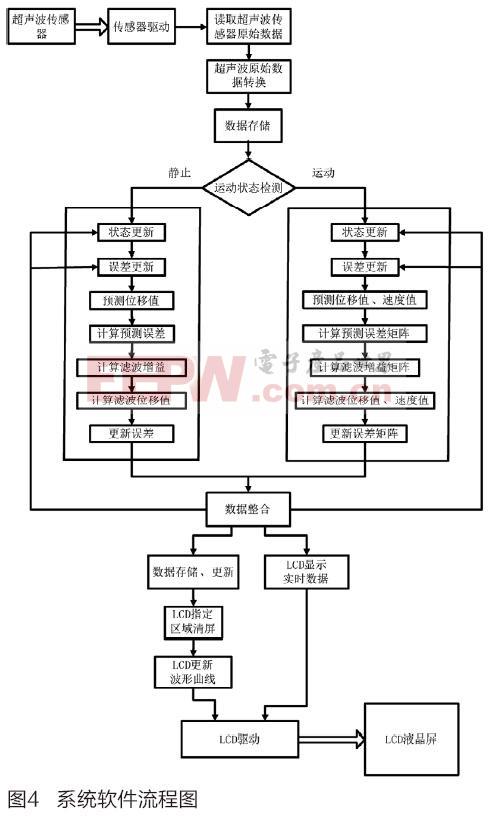
4 滤波参数设置

　　当系统检测到物体处于静止状态时，利用一维卡尔曼滤波算法进行滤波去噪;当系统检测到物体处于运动状态时，则采用多维卡尔曼滤波算法，由于我们采用的超声波传感器的测量范围较小，在短距离变化内，我们可以将运动物体近似看成匀速运动，所以对于运动物体，采用二维卡尔曼滤波算法进行滤波去噪。根据实际系统的噪声和系统调试情况，一维滤波模型和二维滤波模型的系统参数设置如表1所示，其中 为采样时间间隔，由于该系统无额外控制量，所以考虑设计控制矩阵B为零矩阵。

5 应用结果

5.1 输入测量值分析

　　图5是系统的输入测量值，被测量物体首先处于运动状态，由于系统噪声和测量噪声干扰，从该图中可以看到实际测得的物体距离值存在较严重的噪声干扰，上下波动比较大。

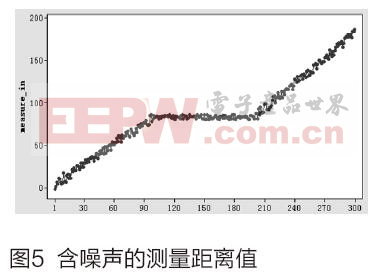
　　随后物体处于静止状态，继而又处于运动状态，我们可以看到在检测过程中，物体距离测量值都有较大的噪声干扰，波动较大，我们使用卡尔曼滤波算法的目的就是对测量值进行去噪处理，以提高系统的测量精度。

5.2 滤波输出数据分析

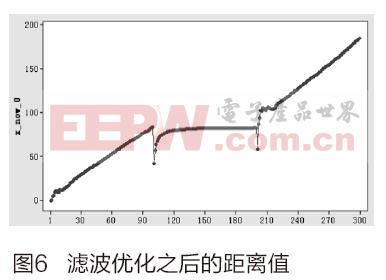
　　图6是经过卡尔曼滤波算法滤波之后的距离数据。卡尔曼滤波算法在工作中，需要一定次数的算法迭代过程才能实现数据收敛，即达到较好的滤波效果。由图6可以看到每当物体运动状态转换后，在经过一定次数的滤波算法迭代后，数据都能达到很好的去噪和收敛效果，对比图5含噪声的测量数据，在精度上有大幅提高。

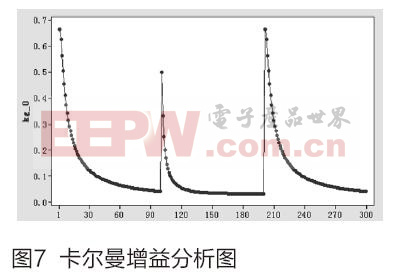
　　卡尔曼增益可以用来衡量卡尔曼滤波算法在工作过程中的去噪效果，在实际的滤波系统中，卡尔曼滤波增益会随着迭代次数的增加而成指数下降，以此来实现滤波去噪的效果。图7展示的是卡尔曼增益的变化过程，我们可以看到在每次运动状态转换后，卡尔曼增益都会快速下降，以使数据收敛。

5.3 性能数据分析

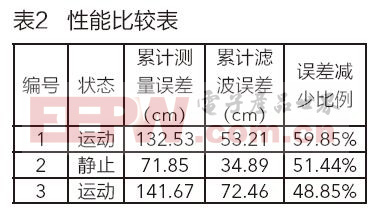
　　表2列出了该系统对测量数据进行滤波处理的性能分析，当系统数据收敛后，我们对数据进行统计整理并列于表2中。由表2可以看出，该系统对噪声有很好的滤波效果，可以大大提高系统的测量精度。

6 总结

　　利用本文提出的设计方法设计实现的超声波雷达测距系统，结合了软件设计方法和硬件设计方法的优势，可以高性能的完成距离的测量，同时，卡尔曼滤波算法的引入，提升了系统的抗干扰能力，大大提高了系统的测量精度。

参考文献：

　　[1]栗素娟, 朱清智, 阎保定. 基于NiosⅡ的机器人视觉伺服控制器的研究与设计[J]. 电子设计应用, 2007, (6):104-105

　　[2]方茁, 彭澄廉, 陈泽文. 基于NIOS的SOPC设计[J]. 计算机工程与设计, 2004, 25(4):504-507

　　[3]王锐, 雷金奎. 基于软核Nios II的SOPC数据采集系统的设计[J]. 计算机测量与控制, 2008, (8)

　　[4]唐思章, 黄勇. SoPC与嵌入式系统软硬件协同设计[J]. 单片机与嵌入式系统应用, 2005, (12):5-8

　　[5]Auger F, Hilairet M, Guerrero J M, et al. Industrial Applications of the Kalman Filter: A Review[J]. Industrial Electronics IEEE Transactions on, 2013, 60(12): 5458-5471

　　[6]Welch G,Bishop G. An Introduction to the Kalman Filter[J]. University of North Carolina at Chapel Hill, 1995