开关电源原理与设计(连载61)

由于单激式开关电源变压器铁芯的磁滞回线面积很小，其磁化曲线基本上可以看成一根直线，导磁率μ也可以看成是一个常数；因此，这里使用平均导磁率 来取代意义广泛的导磁率 。
从图2-18可以看出，磁场强度由H = Hz:和Hx = Hy = 0组成；对于电场强度，其指向平行于Y轴为E = Ey，Ex = Ez = 0。因此，上面两式又可以改写为：

对（2-53）式进行微分，然后代入（2-52）式，即可求得磁场强度的一维分布方程为：

由于加到变压器初级线圈两端的电压是一个直流脉冲方波，在稳定状态条件下，励磁电流产生的磁场强度或磁通密度的增长应与时间成线性关系，即：

当x = 0时，正好位于铁芯片的中心，此处的磁场强度最小，即此点的导数值等于0，由此求得积分常数c1= 0。
对（2-57）再进行一次积分得：

由于在变压器铁芯片内，截面磁场强度的平均值Ha，在任一时间内都必须等于电磁感应所要求的值，即满足（2-45）式的要求，因此对应图2-18对（2-58）式求平均值得：

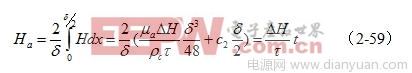
把（2-60）代入（2-58）式，可求得在稳定状态条件下铁芯片中的磁场强度为：

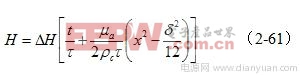
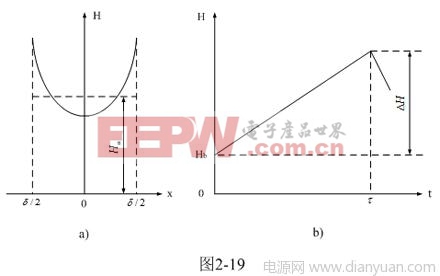
图2-19-a和图2-19-b分别是由（2-61）式给出的，铁芯片中磁场强度按水平方向分布的函数H(x)和按时间分布的函数H(t)曲线图。

从图2-19-a中可以看出，由于涡流产生反磁化作用的缘故，在铁芯或铁芯片中心磁场强度最低，而边缘磁场强度最高。
在图2-19-b中，随着时间线性增长部分是变压器初级线圈励磁电流产生的磁场；Hb是为了补偿涡流产生的去磁场，而由变压器初级线圈另外提供电流所产生的磁场。
从图2-19-b可以看出，涡流损耗对变压器铁芯中磁场强度（平均值）的影响，与变压器正激输出时，次级线圈中电流产生的磁场对变压器铁芯磁场的影响，基本是一样的。值得注意的是，如果用同样方法对y轴方向进行分析，也可以得到同样的结果。
从图2-19-a可以看出，当x =δ/2 时，铁芯片表面磁场强度的最大值为：