轻松了解EMI及其抑制方法
加入技术交流群
几百M都有呢？
我们把同等有效值，同等频率的各种波形做快速傅立叶分析：
蓝色： 正弦波
绿色： 三角波
红色： 方波
可以看到，正弦波只有基波分量，但是三角波和方波含有高次谐波，谐波最大的是方波。
也就是说如果电流或者电压波形，是非正弦波的信号，都能分解出高次谐波。
那么如果同样的方波，但是上升下降时间不同，会怎样呢。同样是100KHz的方波
红色：上升下降时间都为100ns
绿色：上升下降时间都为500ns
可以看到红色的高次谐波明显大于绿色。
我们继续分析下面两种波形，
A: 有严重高频震荡的方波， 比如MOS，二极管上的电压波形。
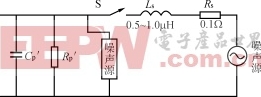
B:用吸收电路，把方波的高频振荡吸收一下。
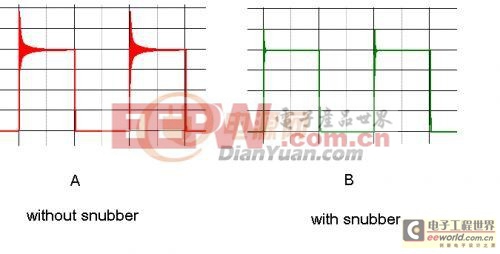
分别做快速傅立叶分析：
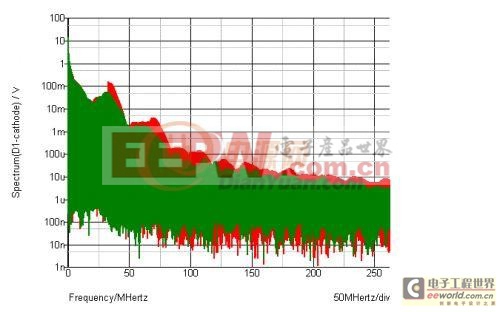
可以看到在振荡频率（大概30M）之后，A波形的谐波，要大于B波形。
再来看，下面的波形，一个是具有导通尖峰的电流波形，一个没有导通尖峰。
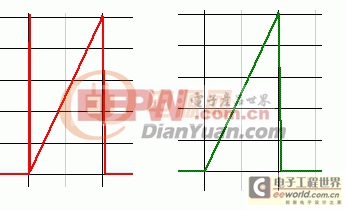对两个波形做傅立叶分析：
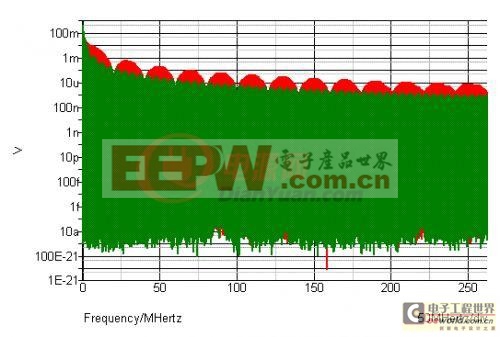
可以看到红色波形的高次谐波，要大于绿色波形。
继续对两个波形，作分析
红色: 固定频率的信号
绿色：具有稍微频率抖动的信号
可以看到，频率抖动，可以降低低频段能量。进一步，放大低频段的频谱能量：
EMC相关文章:EMC是什么意思
评论