自动控制系统的设计--基于根轨迹的串联校正设计

（3）根据公式（6－34）确定夹角 γ：

得到：

（4）由设计要求， ， ， ，求出校正装置的参数。

，

，

得到： ， 。因而超前校正装置的传递函数：

（5）校正后闭环系统的传递函数和主导极点分别为：

G=G0*Gc

Transfer function:

576.8 s + 1921

------------------------------

s^4 + 34 s^3 + 256 s^2 + 384 s

Gl=feedback(G0＊Gc,1)

zpk(Gl)

Zero/pole/gain:

576.8 (s+3.33)

------------------------------------------

(s+25.25) (s+4.745) (s^2 + 4.006s + 16.03)

显然，系统静态误差系数为： ，主导极点为： ，设计基本符合要求。

6.4.2 迟后校正
通过设置校正装置的零极点，使之形成一对在S平面上靠近原点的偶极子，这样，在基本保持原系统主导极点的前提下，可提高系统的静态误差系数而不致使系统的动态性能变坏。

例如，对于一单位反馈系统，若其开环传递函数：G0(S)=K/s(s+a)(s+b),则静态速度误差系数Kv=K/ab ，因为系统主导极点为Sd，则K=|Sd|·|Sd+a|·|Sd+b|。串联迟后校正装置后，开环传递函数：

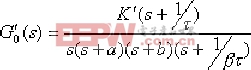若要求主导极点基本不变，则

(6-35)

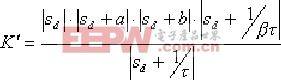由于设计时选取的-1/τ和-1/βτ均靠近原点，因此

,

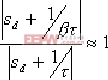但此时

可见校正后静态误差系数增大了约β倍，而主导极点可基本保持不变。

由上，可得出迟后校正的根轨迹法步骤：

（１）画出未校正开环系统的根轨迹；

（２）根据系统设计的时域指标，确定主导极点Sd，进而计算未校正系统的增益Ｋ及静态误差系数Kv ；

（３）将要求的静态误差系统与未校正系统的静态误差系数进行比较；得出迟后校正装置的β值；

（４）确定校正装置的零点和极点。零点的确定方法是：以主导极点Sd为顶点，引线为起起始边，向左旋转5°-10° ，此边与负实轴的交点即为校正装置的零点-1/τ ，由（３）中β值进而确定校正装置极点-1/βτ。

（５）画出校正后系统的根轨迹。若新的主导极点Sd1或静态误差系数与设计要求相关较大，则宜适当调整β或-1/υ ，直至满足要求。

需要说明的是，上述推导过程中按Kv 进行说明，但对于Kp或Ka结论相似。

例6－8 已知一单位反馈控制系统的开环传递函数为

要求校正后的系统能满足下列的性能指标：阻尼比ξ=0.5 ；调整时间ts=10s；静态速度误差系数Kv≥5/s。解：（１）绘制未校正系统的根轨迹如图６—23中的虚线所示。

（２）根据给定的性能指标，确定系统的无阻尼自然频率为

据此，求得希望的闭环主导极点

（３）由根轨迹的幅值条件，确定未校正系统在 处的增益，即根据 ，求得 ,,相应的静态速度误差系数为

（４）基于校正后的系统要求，据此算出迟后校正装置的参数β值，即

考虑到迟后校正装置在 点处产生迟后角的影响，所选取的β值应大于７.5，现取β＝１０。

（５）由点 作一条与线段Ｏ 成 角的直线，此直线与负实轴的交点就是校正装置的零点，由图６—23 可知，零点 ，极点为 。这样，校正装置的传递函数

校正后系统的开环传递函数

校正后系统的根轨迹如图６—23中的实线所示。由该图可见，若要使 ，则校正后系统主导极点的位置略偏离要求值，即由 点移到