一文搞懂《扩展卡尔曼滤波融合IMU和ODOM》

作者：时间：2025-07-29 来源：硬十

加入技术交流群
- 扫码加入
  和技术大咖面对面交流
  海量资料库查询

1、什么是卡尔曼滤波？

卡尔曼滤波（Kalman filtering）是一种利用线性系统状态方程，通过系统输入输出观测数据，对系统状态进行最优估计的算法。由于观测数据中包括系统中的噪声和干扰的影响，所以最优估计也可看作是滤波过程。

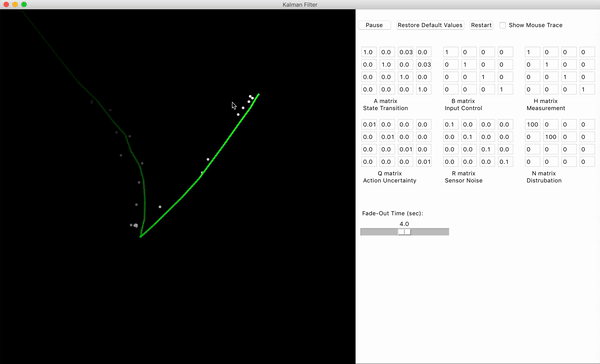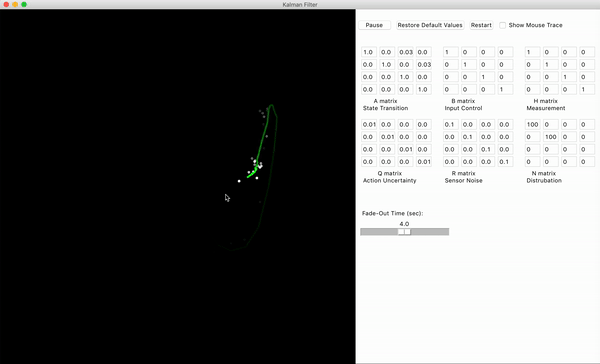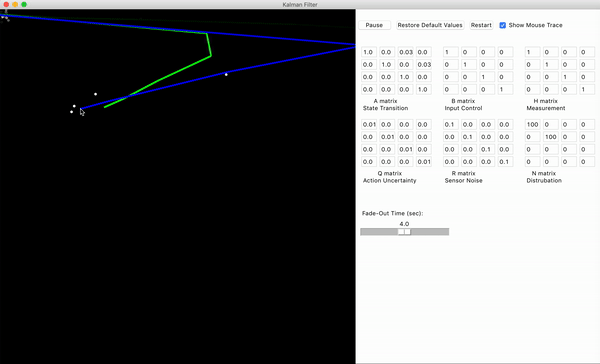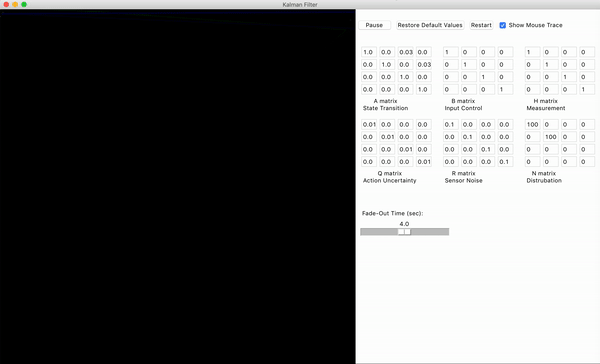
就像移动靶在运动中，每一刻都有 “实际在哪”“跑多快”“往哪个方向拐” 这些真实状态（对应系统状态向量x）。但狙击手看不到这些 “真实值”，只能通过瞄准镜（传感器）得到带误差的观测（比如 “好像在 100 米处，可能偏左半米”）。

观测数据里的 “噪声和干扰”，就像瞄准镜前的树叶、雾气、树木遮挡

当树叶挡住视线时（观测数据突然不准），卡尔曼滤波不会完全相信这一帧的观测，而是更多依赖 “基于目标运动规律的预判”（比如 “刚才目标在匀速跑，不可能突然跳 10 米，这帧数据肯定是被树叶挡了，忽略它”）。

当视线清晰时（观测可靠），滤波会用新观测修正之前的预判（比如 “果然在 105 米，和我想的差不多，稍微调一下瞄准点”）。

卡尔曼滤波就像一个经验丰富的狙击手：用目标的运动规律（系统模型）做预判，用带噪声的观测（传感器数据）做修正，最终在干扰中锁定真实位置。这个过程既不盲目相信单次观测（过滤噪声），也不固执依赖历史判断（结合新信息），从而实现 “最优估计”。

2、扩展卡尔曼滤波（EKF）和卡尔曼滤波（KF）

卡尔曼最初提出的滤波理论只适用于线性系统,Bucy，Sunahara等人提出并研究了扩展卡尔曼滤波(Extended Kalman Filter，简称EKF)，将卡尔曼滤波理论进一步应用到非线性领域。EKF的基本思想是将非线性系统线性化，然后进行卡尔曼滤波，因此EKF是一种次优滤波。其后，多种二阶广义卡尔曼滤波方法的提出及应用进一步提高了卡尔曼滤波对非线性系统的估计性能。二阶滤波方法考虑了Taylor级数展开的二次项，因此减少了由于线性化所引起的估计误差，但大大增加了运算量，因此在实际中反而没有一阶EKF应用广泛。

EKF全称ExtendedKalmanFilter，即扩展卡尔曼滤波器，一种高效率的递归滤波器(自回归滤波器)。

扩展卡尔曼滤波（EKF）是卡尔曼滤波（KF）的 “升级版”，专门用来解决卡尔曼滤波搞不定的场景。我们可以继续用 “狙击枪瞄准移动靶” 的比喻来理解它们的关系：

1. 卡尔曼滤波（KF）：只能对付 “规矩的目标”

卡尔曼滤波的核心前提是：目标的运动规律是 “线性的”。
比如移动靶在匀速直线运动（速度不变、方向不变），或者匀加速运动（每秒多跑 1m/s）—— 这些运动可以用简单的线性公式描述（比如 “下一秒位置 = 现在位置 + 速度 × 时间”）。
这时候，狙击手只要用 “匀速 / 匀加速模型” 就能精准预判，卡尔曼滤波的公式也能直接套用，计算简单又高效。

2. 扩展卡尔曼滤波（EKF）：能搞定 “调皮的目标”

但现实中，很多目标的运动是 “非线性的”：

比如移动靶突然转弯、绕圈，甚至做 S 形走位（运动方向和速度的关系不是简单的线性公式）；
或者传感器的观测方式是非线性的（比如用雷达测角度，角度和位置的关系是三角函数，不是直线关系）。

这时候，卡尔曼滤波就失效了 —— 因为它的公式只能处理线性关系，面对转弯的目标，用 “匀速直线” 模型预判会偏差越来越大。

EKF 的作用就是 “把非线性问题掰弯了变成线性的”：
它会在 “当前估计的状态点” 附近，用一条直线（切线）近似目标的非线性运动轨迹（就像用很多小线段拼接成曲线）。这样一来，就能继续套用卡尔曼滤波的线性公式来计算，只不过每次都要重新算这条 “切线”（专业上叫 “线性化”，用雅克比矩阵实现）。

总结：关系就像 “基础款计算器” 和 “科学计算器”

卡尔曼滤波是 “基础款”：只能算加减乘除（线性问题），简单直接，速度快。
扩展卡尔曼滤波是 “科学计算器”：能处理三角函数、指数等复杂运算（非线性问题），通过 “近似线性化” 扩展了适用范围，但计算更复杂一点。
两者的核心逻辑（“预判 + 修正” 的滤波思想）完全一致，只是 EKF 能应对更贴近现实的非线性场景。

3、EKF融合IMU和ODOM的计算过程

咱们可以把 EKF 融合 IMU 和 ODOM 的过程，想象成一个 “猜位置” 的游戏，你需要结合两种 “线索” 来不断修正自己的猜测，让结果越来越准。

IMU（Inertial Measurement Unit）和 ODOM（Odometry）在机器人领域以及其他涉及运动感知和定位的系统中是非常重要的概念，以下是它们的详细介绍：

IMU（惯性测量单元）

定义
IMU 是一种能够测量物体三轴加速度和三轴角速度的组合式传感器，有的 IMU 还集成了磁力计，可以测量物体的磁场信息，辅助确定物体的方向。它是一个小型化、高度集成的系统，能够实时提供物体的运动状态信息。
工作原理

加速度计
：基于牛顿第二定律，通过检测内部质量块在加速度作用下产生的力，来测量加速度。比如，当物体加速时，质量块会相对于传感器内部的固定结构产生位移，通过检测这种位移并将其转换为电信号，就可以得到加速度的大小和方向。
陀螺仪
：利用科里奥利力原理工作。当陀螺仪的壳体发生旋转时，内部的旋转质量块会受到科里奥利力的作用，从而产生微小的振动或偏移，通过检测这些变化就可以测量出角速度。

ODOM（里程计）

定义
里程计是一种用于测量物体在运动过程中移动距离和方向的装置或算法，通过对运动过程中的一些参数进行累计和计算，来确定物体的位置变化。
工作原理

轮式里程计
：常见于轮式机器人，通过安装在轮子上的编码器来记录轮子的转动圈数。结合轮子的半径，就可以计算出机器人在平面上移动的距离。同时，通过一些额外的传感器（如安装在差速驱动机器人两个轮子上的编码器，对比两个轮子的转动圈数差异），可以推算出机器人的转向角度和方向变化。

先给两个 “线索源” 做个简单画像：

IMU：像你身上的 “运动传感器”，能实时感觉到自己在怎么动 —— 比如走得快还是慢、有没有转弯（用角速度测转弯，用加速度测加速）。但它有个毛病：猜多了会 “跑偏”（比如站着不动，它可能会慢慢觉得你在挪位置，这叫 “漂移”）。
ODOM：像你手里的 “路标导航”，每隔一会儿告诉你当前的位置和速度（比如轮式里程计通过轮子转了多少圈算位置，或者视觉里程计通过摄像头看环境算位置）。它相对稳定，不会轻易跑偏，但更新没那么快（比如轮子转半圈才出一次数据），而且偶尔会 “骗你”（比如轮子打滑时，它算的位置就不准了）。

EKF 做的事，就是用 IMU 的 “实时感觉” 先“猜”，再用 ODOM 的 “路标信息” 来修正，最后得到一个又快又准的结果。具体分两步：

第一步：用 IMU “猜”（预测阶段）

假设你现在要走路去超市，EKF 先根据 IMU 的信息，实时猜你每一秒的位置和速度。比如：

上一秒你在 “小区门口”（上一时刻的位置），速度是 “1 米 / 秒向前”（上一时刻的速度）。
这一秒 IMU 告诉你：“你没转弯（角速度为 0），也没加速（加速度为 0）”（IMU 的测量值）。
那 EKF 就会猜：“这一秒你应该在小区门口往前 1 米的地方，速度还是 1 米 / 秒”（预测的当前位置和速度）。

但 EKF 知道 IMU 会 “跑偏”，所以猜的时候会留个 “误差范围”：比如 “位置大概在 1 米左右，误差可能有 0.5 米”（这个误差会随着 IMU 用得越久慢慢变大，就像猜多了越来越没谱）。

第二步：用 ODOM “修正”（更新阶段）

走了一会儿，ODOM 这个 “路标” 说话了：“根据轮子转的圈数，你现在应该在‘离小区门口 1.2 米’的地方”（ODOM 的测量值）。

这时候 EKF 要做两件事：

对比 “猜的位置（1 米）” 和 “ODOM 说的位置（1.2 米）”，算出差了 0.2 米。
看看这两个线索谁更可信，再决定怎么修正。

比如：

如果地面很平，轮子没打滑，ODOM 很靠谱（权重高），那就多听 ODOM 的，把猜测从 1 米调成 1.15 米（靠近 1.2 米）。
如果地面坑坑洼洼，轮子可能打滑了，ODOM 不太准（权重低），就少听 ODOM 的，调成 1.05 米（靠近原来的猜测）。

修正后，误差范围也会缩小（比如从 0.5 米变成 0.2 米），因为两个线索交叉验证了，结果更靠谱了。

循环往复，越猜越准

之后就重复这两步：

没 ODOM 数据时，用 IMU 实时猜（预测），误差慢慢变大；
有 ODOM 数据时，用它修正猜测（更新），误差缩小。

这样一来，既利用了 IMU “反应快” 的优点（实时跟紧运动），又用 ODOM “不跑偏” 的优点（修正累积误差），最后得到的位置、速度就会又快又准。

简单说，EKF 就像个 “聪明的裁判”：

让 IMU 当 “实时报信员”，随时喊 “现在往哪动、动多快”；
让 ODOM 当 “定期校准员”，每隔一会儿喊 “实际位置在这”；
裁判根据两者的靠谱程度，综合出一个最准的结果。

4、晦涩难懂的预测公式

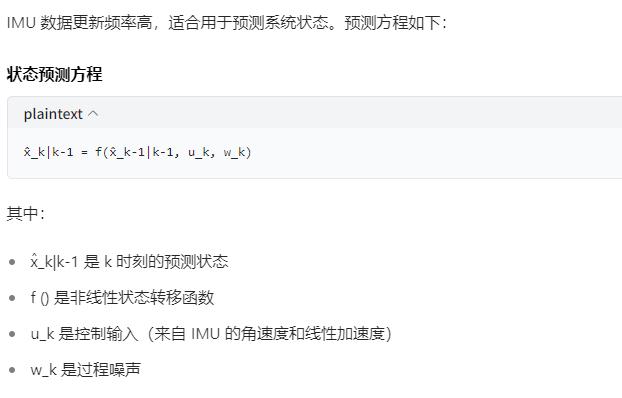
这个方程是扩展卡尔曼滤波器（EKF）的核心预测方程，确实比较抽象。我来一步步解释，让它变得更容易理解。

状态预测方程的直观理解

这个方程描述了如何根据上一时刻的状态估计和当前的控制输入，来预测当前时刻的系统状态。

我们可以用一个生活中的例子来类比：

上一时刻的状态：就像你现在知道自己的位置和速度

控制输入：就像你知道自己正在向前走，或者正在转弯

预测的状态：基于现在的位置、速度和动作，预测出下一刻你会在哪里

数学符号详细解释

让我们拆解这个方程：

符号含义：

x̂：带帽子的 x 表示 "估计值"（不是真实值，因为有误差）
k|k-1：竖线后面的数字表示 "基于哪个时刻的信息"

x̂_k|k-1
表示：基于 k-1 时刻的信息，对 k 时刻状态的预测
x̂_k-1|k-1
表示：基于 k-1 时刻的信息，对 k-1 时刻状态的估计（这是上一轮更新得到的结果）

f()：这是一个函数，表示状态如何从一个时刻转移到下一个时刻
u_k：控制输入，例如 IMU 测量的加速度和角速度
w_k：过程噪声，表示系统的不确定性（例如，你的动作可能不完全按照计划执行）

更具体的例子：移动机器人

假设我们有一个在平面上移动的机器人，它的状态包括：

位置：x, y
朝向：θ（角度）
速度：v_x, v_y（x 和 y 方向的速度）

总结

状态预测方程x̂_k|k-1 = f(x̂_k-1|k-1, u_k, w_k)的核心思想是：

基于上一时刻的状态估计
加上控制输入的影响
考虑系统的不确定性
预测当前时刻的状态

通过这个方程，EKF 能够利用 IMU 等高频率的控制输入数据，不断预测系统的状态变化。

5、过程噪声协方差矩阵

过程噪声协方差矩阵

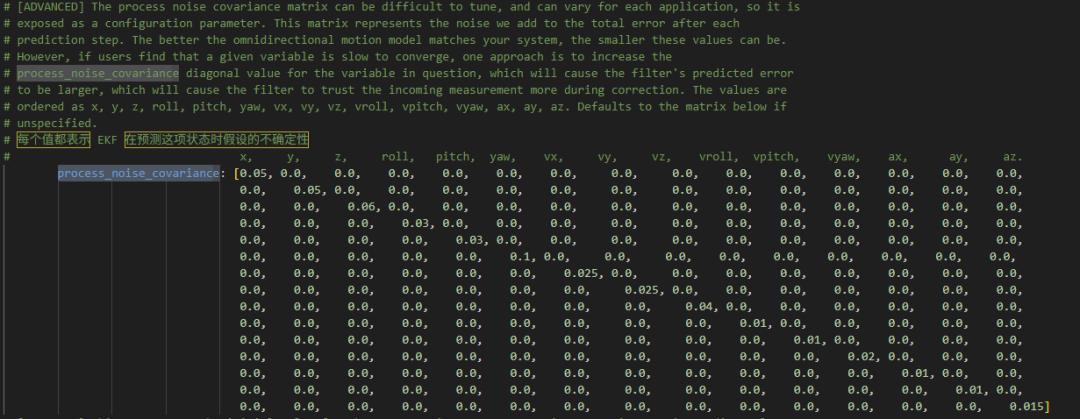
1. 矩阵结构与状态对应

矩阵的行和列严格对应 EKF 状态向量的顺序，通常是：
[x, y, z, roll, pitch, yaw, vx, vy, vz, vroll, vpitch, vyaw, ax, ay, az]

每个元素 process_noise_covariance[i][j] 的含义：

当 i=j（对角线元素）：表示单个状态量的预测噪声强度（不确定性大小）。
当 i≠j（非对角线元素）：表示两个状态量之间的噪声相关性（通常设为 0，假设各状态噪声独立）。

2. 逐行 / 列解读（以你的配置为例）

下面结合常见机器人运动场景（如差速底盘、机械臂），解释对角线元素（非对角线多为 0，代表噪声独立）的物理意义：

状态维度	索引	对角线值	含义（预测时的不确定性）
位置	x	0.05	预测 x 方向位置时，假设的噪声强度（比如机器人在 x 轴运动，模型误差导致的位置偏差 “大概这么大”）
	y	0.05	y 方向位置的预测噪声
	z	0.06	z 方向位置（高度）的预测噪声（若机器人是地面移动设备，z 变化少，噪声可更小；若涉及飞行则需调大）
姿态（角）	roll	0.03	横滚角（roll）的预测噪声（比如模型假设 “姿态不变”，但实际因振动等导致的误差）
	pitch	0.03	俯仰角（pitch）的预测噪声
	yaw	0.1	偏航角（yaw）的预测噪声（地面机器人转向时，yaw 易受干扰，噪声通常更大）
线速度	vx	0.025	x 方向线速度的预测噪声（模型假设 “匀速”，但实际加减速、打滑会导致误差）
	vy	0.025	y 方向线速度的预测噪声
	vz	0.04	z 方向线速度（高度变化率）的预测噪声
角速度	vroll	0.01	横滚角速度的预测噪声
	vpitch	0.01	俯仰角速度的预测噪声
	vyaw	0.02	偏航角速度的预测噪声（转向时角速度易波动，噪声通常高于其他轴）
线加速度	ax	0.01	x 方向线加速度的预测噪声（加速度计本身有噪声，模型外推也会引入误差）
	ay	0.01	y 方向线加速度的预测噪声
	az	0.015	z 方向线加速度的预测噪声（受重力影响，若用于地面设备，az 需覆盖 “静止时 1g” 的误差）