设计三次谐波峰值F类放大器以实现最高效率

我们探讨了如何在F类放大器中添加少量的电压纹波来提高其效率，然后通过一个设计示例进行工作。

F类放大器可视为B类放大器的一种特殊变体。与B类放大器的线性操作不同，它将晶体管作为开关驱动。F类放大器还修改负载网络在谐波频率下的阻抗，以调整晶体管两端的电压波形。当集电极电流高时，添加适量的不同谐波分量可以使集电极电压尽可能低。

在上一篇文章中，我们看到使用三次谐波分量产生最大平坦波形可以将放大器的效率从78.5%（B类放大器）提高到88.4%（三次谐波峰值F类放大器）。“最大平坦”一词是指波形的导数在峰值处为零

然而，事实证明，最大平坦的波形并不能产生最佳效率。在本文中，我们将探讨如何允许电压波形具有少量纹波，以进一步提高三次谐波峰值放大器的效率。

集电极电压波形实验

三次谐波峰值F类放大器的集电极电压波形可以表示为：

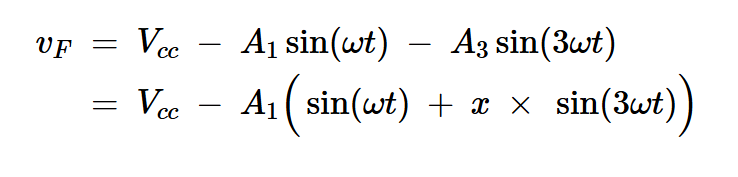
方程式1

解释：

A3是三次谐波分量

A1是基本组成部分

x是三次谐波分量与基波分量的比率（x=A3/A1）。

对于小于或等于1/9的x值，波形呈现单峰和谷。在x=1/9时，实现了最大的平坦波形。当x超过1/9时，波形开始过冲并呈现双峰。

为了说明这一点，图1显示了A1=Vcc=1V和三个不同x值的F类集电极电压波形（vF）：

x=0（红色曲线）。

x=1/9（蓝色曲线）。

x=1/7（绿色曲线）。

由于对于x的所有三个值，A1=1 V，我们还可以将图1中的波形视为表示不同三次谐波分量值的总集电极电压。

三个x值的F类集电极电压波形。

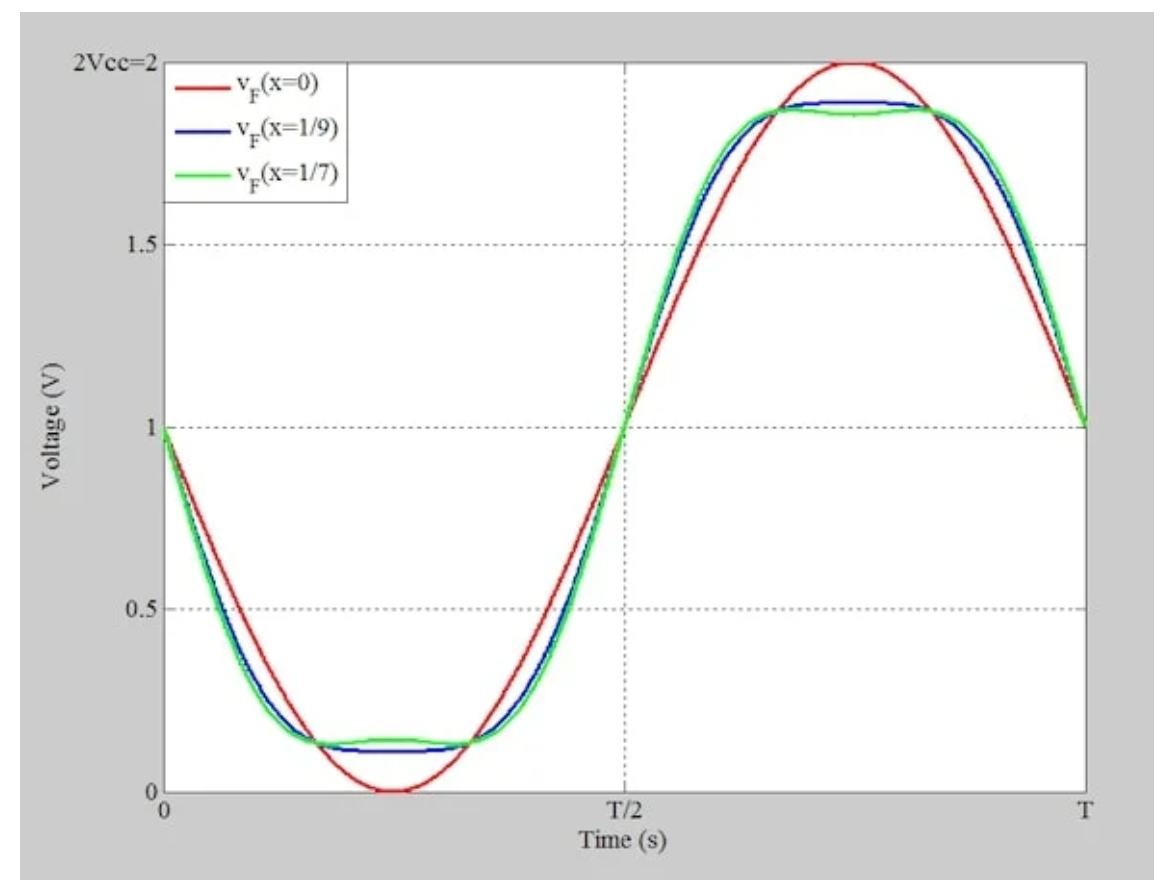
图1 A1=Vcc=1V和x=0、1/9和1/7的总集电极电压

正如我们在前面的一篇文章中讨论的那样，添加三次谐波分量可以减少vF的峰间摆动。上面清楚地说明了这一点——没有三次谐波的红色曲线从0到2Vc（2Vcc）摆动。相比之下，蓝色曲线（x=1/9，最大平坦波形）从0.11V摆动到1.89V。

F类操作的这一关键特性使我们能够使用超过电源电压设置的正常摆动限制的基频分量。然后，我们可以增加基频的输入功率，以充分利用潜在的摆动，从而为负载提供更大的功率。

这就把我们带到了绿色曲线，它使用了比最大平坦波形更大的三次谐波，并且似乎具有更小的峰间摆动。图2提供了曲线的放大视图，以便我们可以更好地看到波形的摆动减小。

放大三个不同x值的电压摆动。

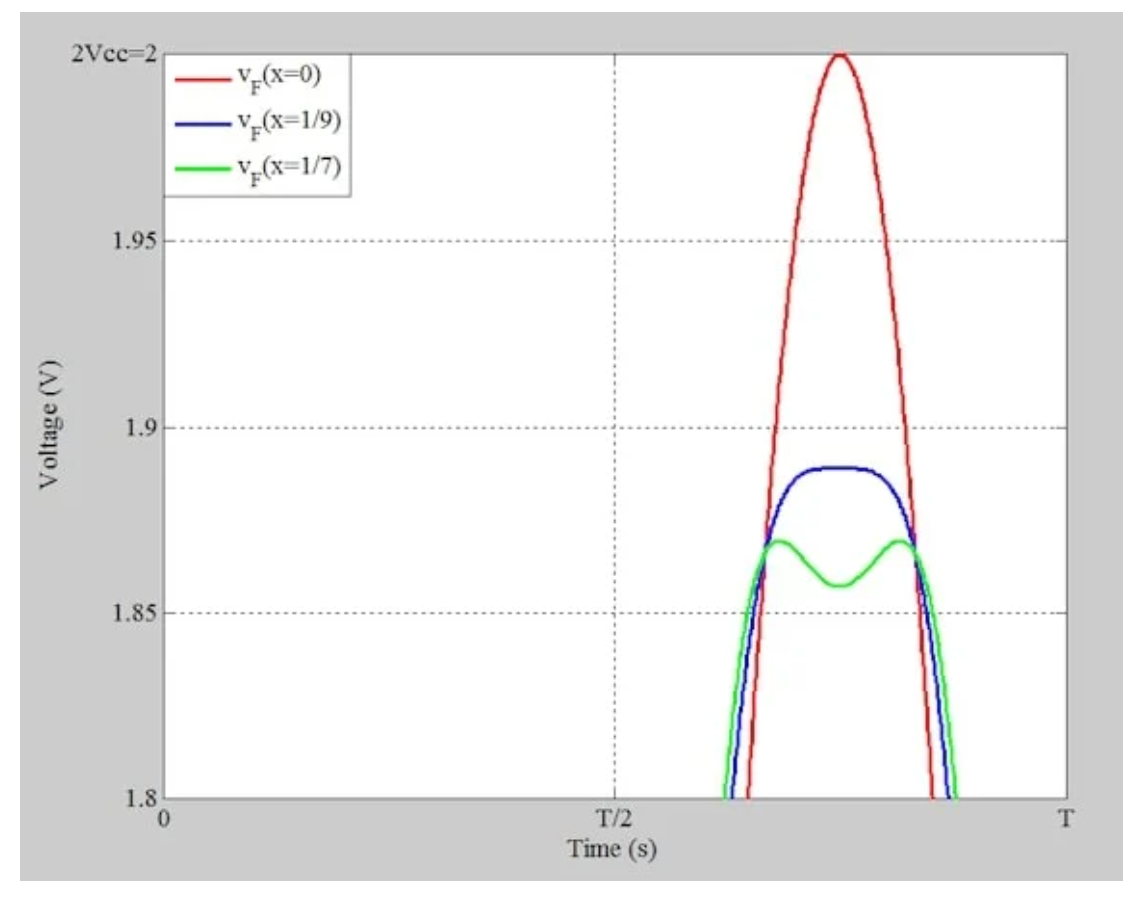
图2 A1=Vcc=1V和x=0、1/9和1/7的总集电极电压的放大视图

图1和图2表明，电压波形中的少量纹波可能使我们能够增加基波分量的功率。这反过来又可以通过增加输送到负载的功率来提高放大器的性能。

但是“少量”是多少呢？在下一节中，我们将推导出具有最大效率的三次谐波峰值F类放大器的方程。然而，在开始之前，让我们通过将x调整为1/4来对这些波形进行最后一次测试。新波形在图3中以青色显示。

新的、更高的x值的电压摆动。

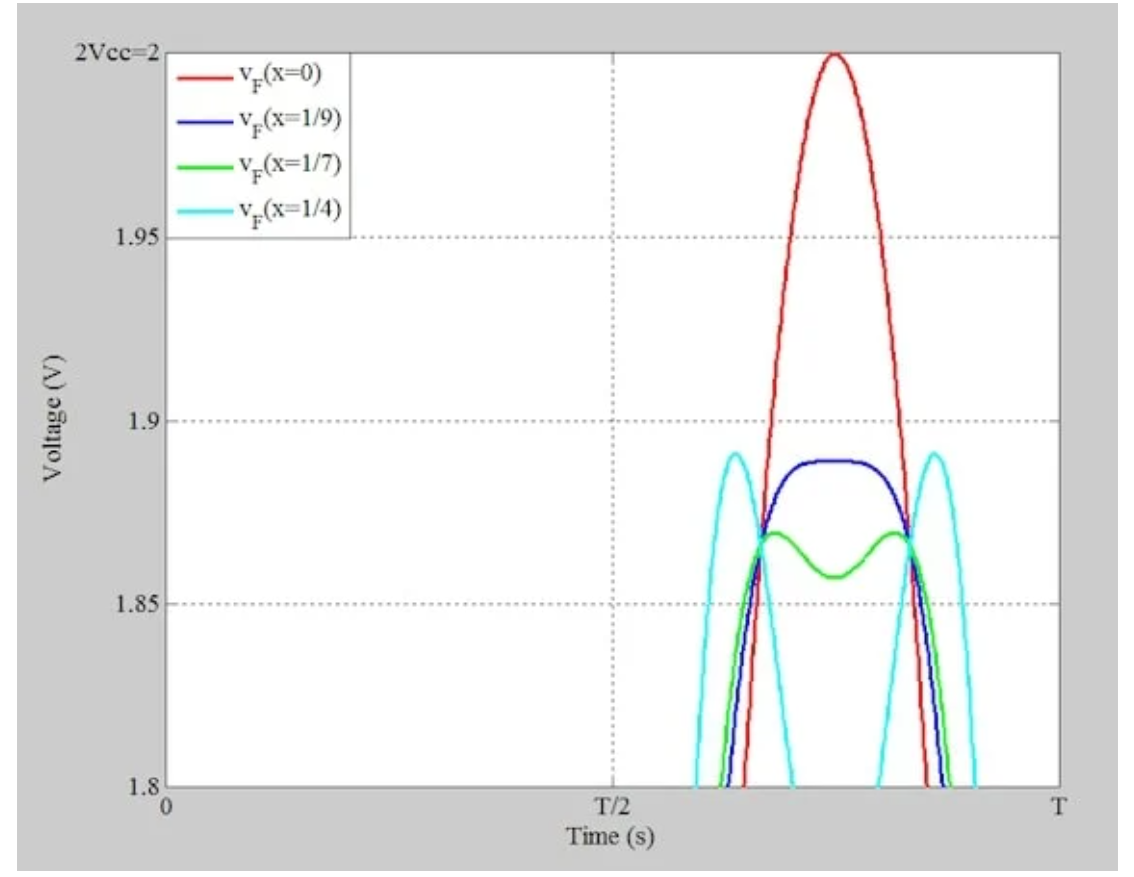
图3 A1=Vcc=1V和x=0、1/9、1/7和1/4的总集电极电压的放大视图

再次，增加x的值会导致峰值超过最大平坦波形的峰值。这证实了必须存在使效率最大化的x的最佳值，并且该值大于1/9（最大平坦波形的值）。

推导最大效率方程

图4显示了三次谐波峰值F类放大器的电路图。为了找到该放大器的最佳x值，我们需要了解放大器的效率如何受到波形峰间摆动的影响。

三次谐波峰值F类放大器的电路图。

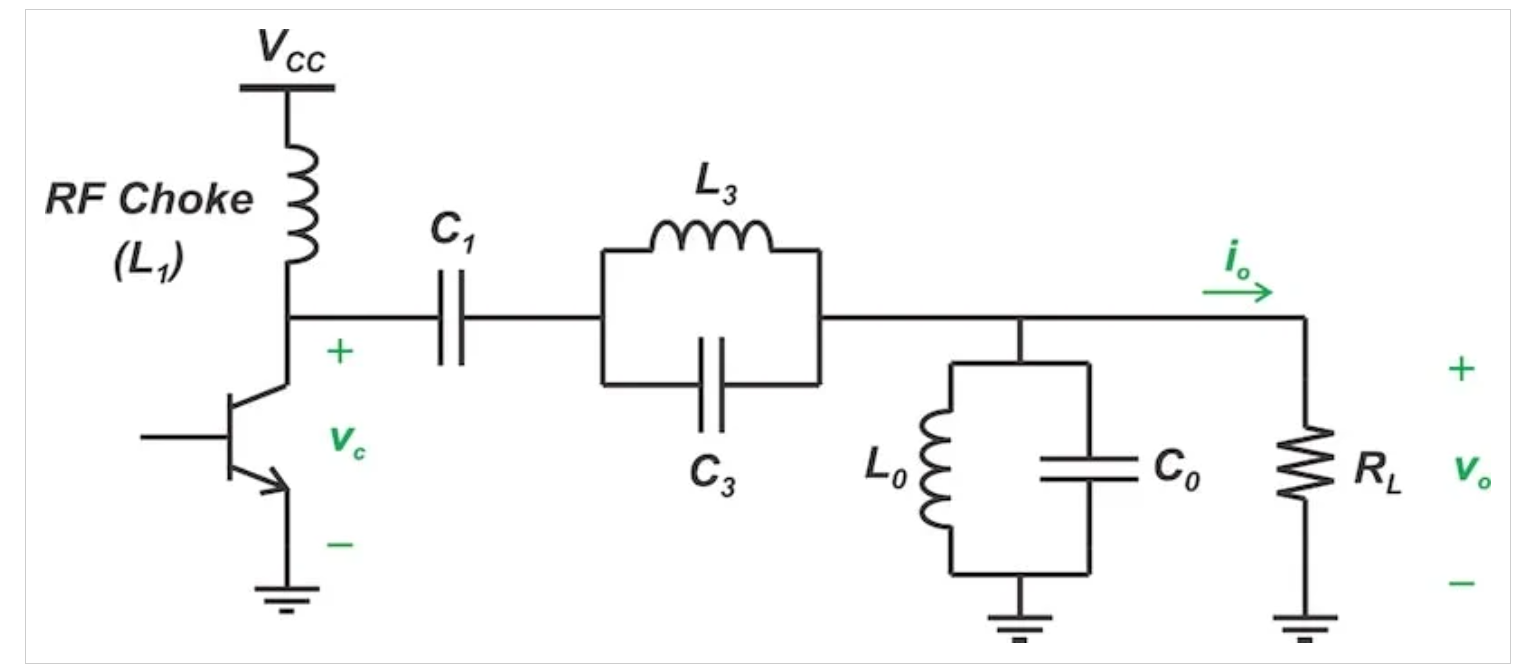
图4 三次谐波峰值F类放大器

回想一下，功率放大器的效率定义为：

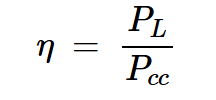
方程式2

解释：

PL是输送到负载的平均功率

Pcc是从电源汲取的功率。

输送到负载的功率为：

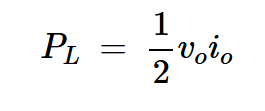
方程式3

其中vo和io分别是负载两端的电压和通过负载的电流的振幅。

为了计算电源提供的功率，我们找到从电源汲取的电流的平均值（Ic，ave），并将其乘以电源电压（Vcc）：

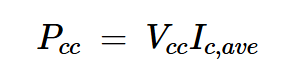
方程式4

将方程3和4代入效率方程，我们得到：

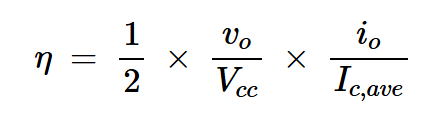
方程式5

F类放大器中的导通角通常设置为180度，就像B类操作一样。在导通角为180度的情况下，我们可以假设集电极电流是振幅为Ip、周期为T的半波整流正弦波，如图5所示。

导通角为180度时的集电极电流波形。

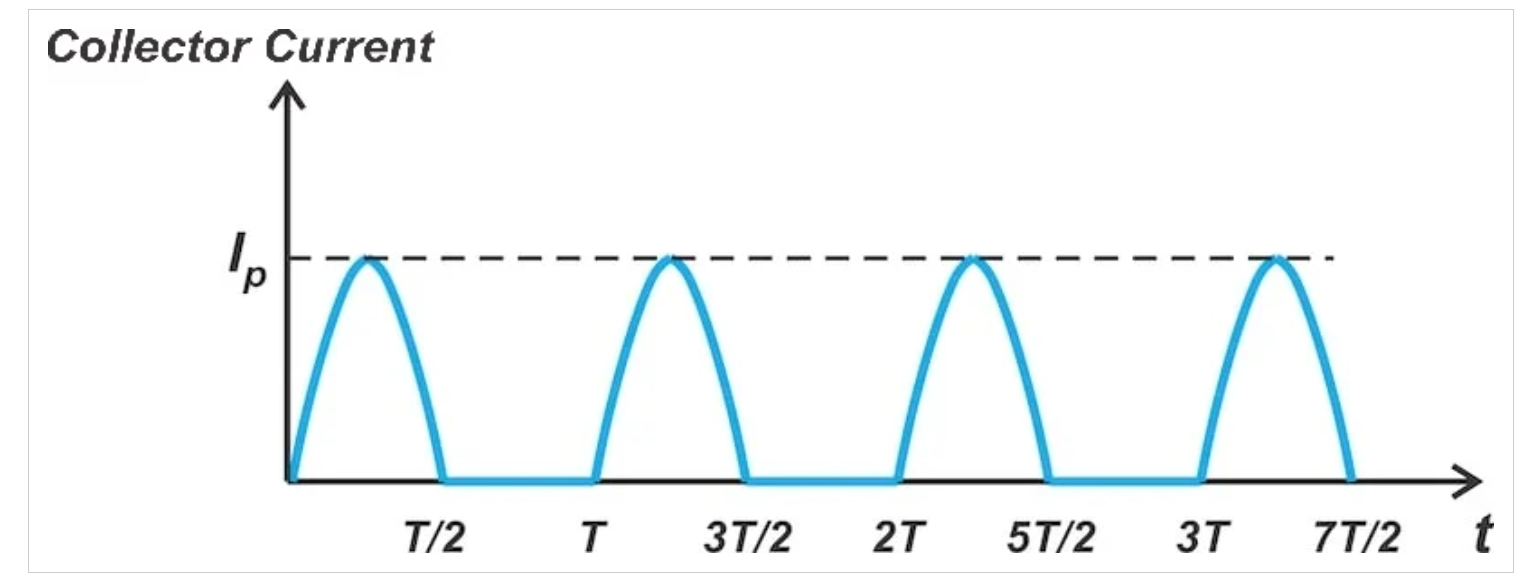
图5 集电极电流是半波整流正弦曲线

使用傅里叶级数表示，上述波形可以表示为：

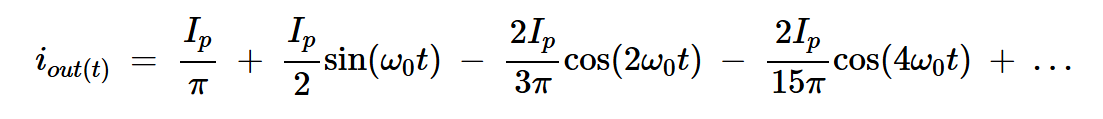
方程式6

使用上述方程，我们可以建立从电源汲取的直流电流和通过负载的基波电流的关系：

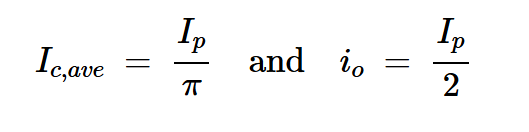
方程式7

我们不知道上述方程中Ip的值。然而，我们现在有足够的信息来简化效率方程（方程5），从而得出：

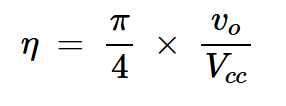
方程式8

我们将在下一节中了解更多关于上述方程的信息。

评估效率方程

方程式8建立了输出电压摆动与放大器效率之间的简单关系。该方程的基本假设是导通角为180度，这意味着集电极电压波形是半波整流正弦波。因此，该方程应适用于B类放大器和最大平坦的F类放大器。

让我们核实一下这句话的真实性。B类放大器中输出摆幅的最大幅度为vo=Vcc。将此应用于方程8，B类放大器的最大效率为其广为人知的π/4值，计算如下：

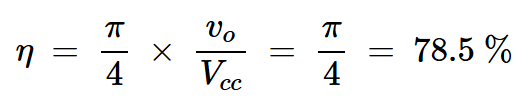
方程式9

对于最大平坦的F类放大器，集电极电压方程（方程1）的参数为x=1/9和A1=9Vcc/8。因此，效率方程简化为：

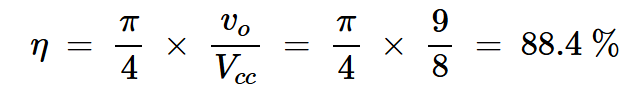
方程式10

这与前一篇文章中提供的分析是一致的。

三次谐波峰值F类放大器的最大效率

现在我们已经确认了新效率方程的有效性，让我们使用它。方程式8显示，当输出电压摆动与电源电压的比率（vo/Vcc）也达到最大时，效率达到最大。输出摆幅由基波分量（A1）的振幅决定。因此，对于给定的电源电压，我们需要找到允许我们最大化A1的三次谐波（A3）的值。

我们将绕过这里的详细数学分析，直接概述最大效率的条件。当满足以下条件时，三次谐波峰值放大器的效率达到最大：

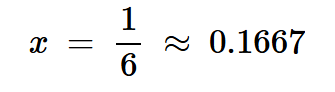
方程式11

其中x=A3/A1。在这种情况下，将最小集电极电压设为零（vF=0），我们得到A1和A3在电源电压方面的绝对值：

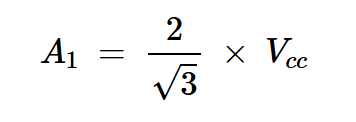
方程式12

以及：

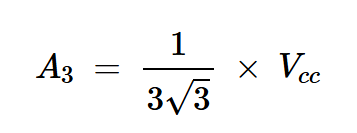
方程式13

图6绘制了最佳有效电压波形。为了进行比较，还包括x=0的波形。

最高效率三次谐波峰值F类放大器的集电极电压波形。

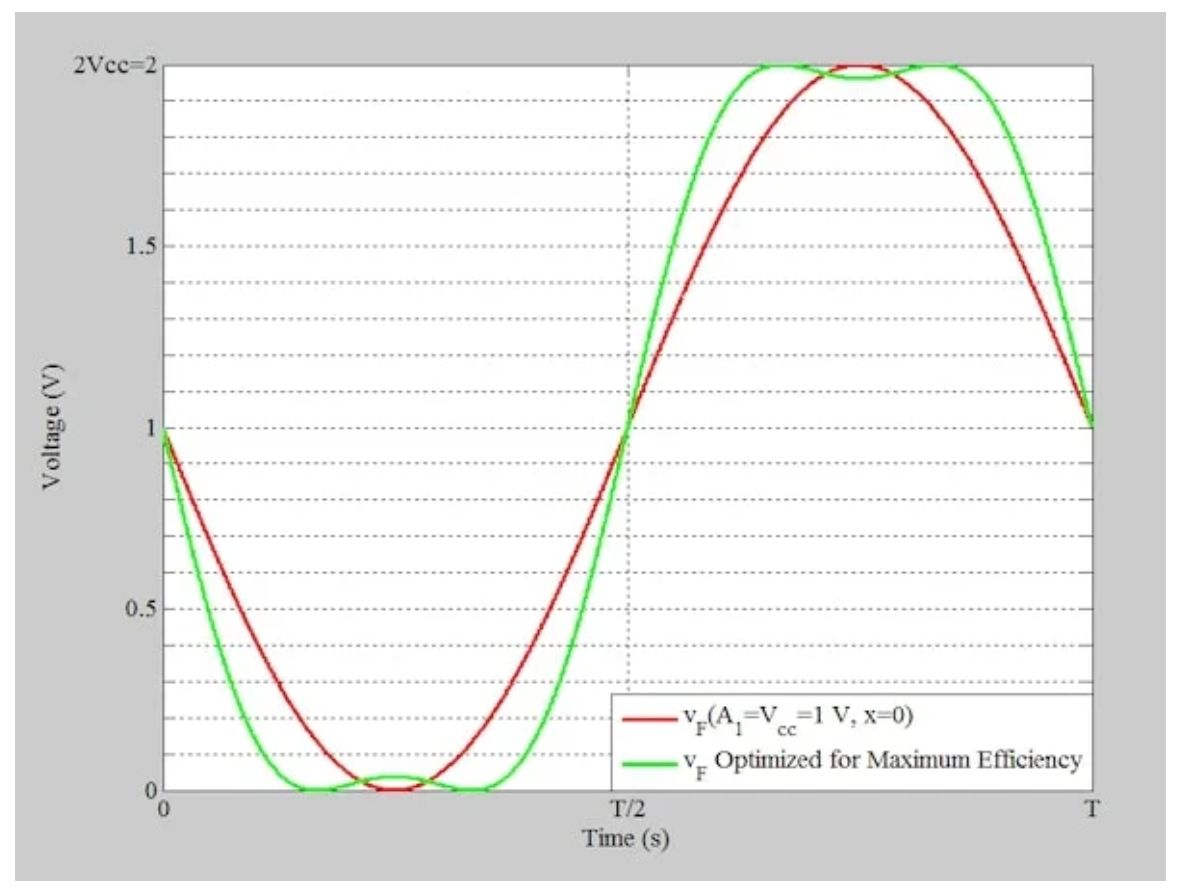
图6 绿色曲线显示了最大效率放大器的集电极电压波形（A1=Vcc=1V，x=1/6）

方程12建立了最大效率三次谐波峰值放大器的A1和Vcc之间的关系。将该方程与我们之前推导的效率方程（方程8）相结合，我们现在可以确定可实现的效率：

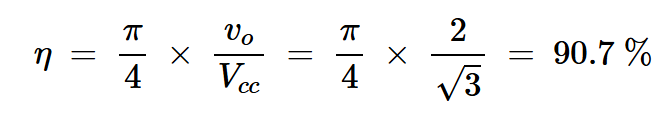
方程式14

添加电压纹波后，三次谐波峰值F类放大器的最大效率为90.7%。

示例：设计三次谐波峰值放大器以实现最高效率

设计了一种具有三次谐波峰值的F类放大器，以实现最高效率。对于PL=10 W的输出功率和Vcc=12 V的电源电压，确定以下内容：

负载电阻（RL）。

晶体管必须承受的最大电流和电压。

我们可以使用放大器输出功率的方程来计算负载电阻（RL）。输出功率可以通过以下公式计算：

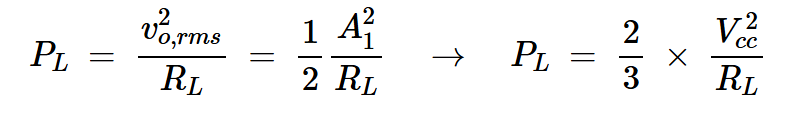
方程式15

在上述方程式中，我们用方程式12中的A1值进行了替换。当PL=10 W和Vcc=12 V时，我们得到RL=9.6Ω。

最大集电极电压为2Vcc，在这种情况下=24V。为了确定最大集电极电流（Ip），我们注意到基波集电极电流的幅度为Ip/2。该电流流入负载（RL），并产生基波电压振幅$A_1=\left(\frac{2}{\sqrt{3}}\right)V_{cc}$.

因此，我们有：

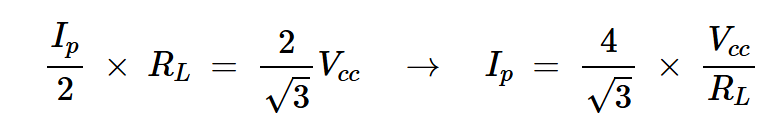
方程式16

将我们的示例值代入这个方程，我们得到Ip=2.89 A。

总结

正如我们现在所看到的，三次谐波峰值F类放大器的最大理论效率为η=90.7%。在下一篇文章中，我们将了解一种不同的F类放大器配置，即传输线峰值F类放大器，它可以进一步提高效率。