理解传输线峰值F类放大器

了解此功率放大器如何使用四分之一波长传输线实现高达100%的效率。

到目前为止，我们对F类功率放大器的讨论主要围绕三次谐波峰值放大器展开。这种F类配置包含一个三次谐波分量，使其集电极电压波形类似于方波，从而提高了效率和输出功率。正如我们在上一篇文章中所了解到的，三次谐波峰值放大器的最大效率为90.7%。

我们可以通过调整所有高次谐波分量来提高效率，而不仅仅是第三谐波分量。在这篇文章中，我们将了解一个专门为实现这一目标而设计的F类放大器。它被称为传输线峰值放大器，在理想条件下具有100%的效率，广泛应用于VHF（30至300 MHz）和UHF（300 MHz至3 GHz）FM无线电发射机。

传输线峰值放大器的电路图如图1所示。如您所见，其负载网络由并联谐振电路和基频四分之一波长传输线组成。

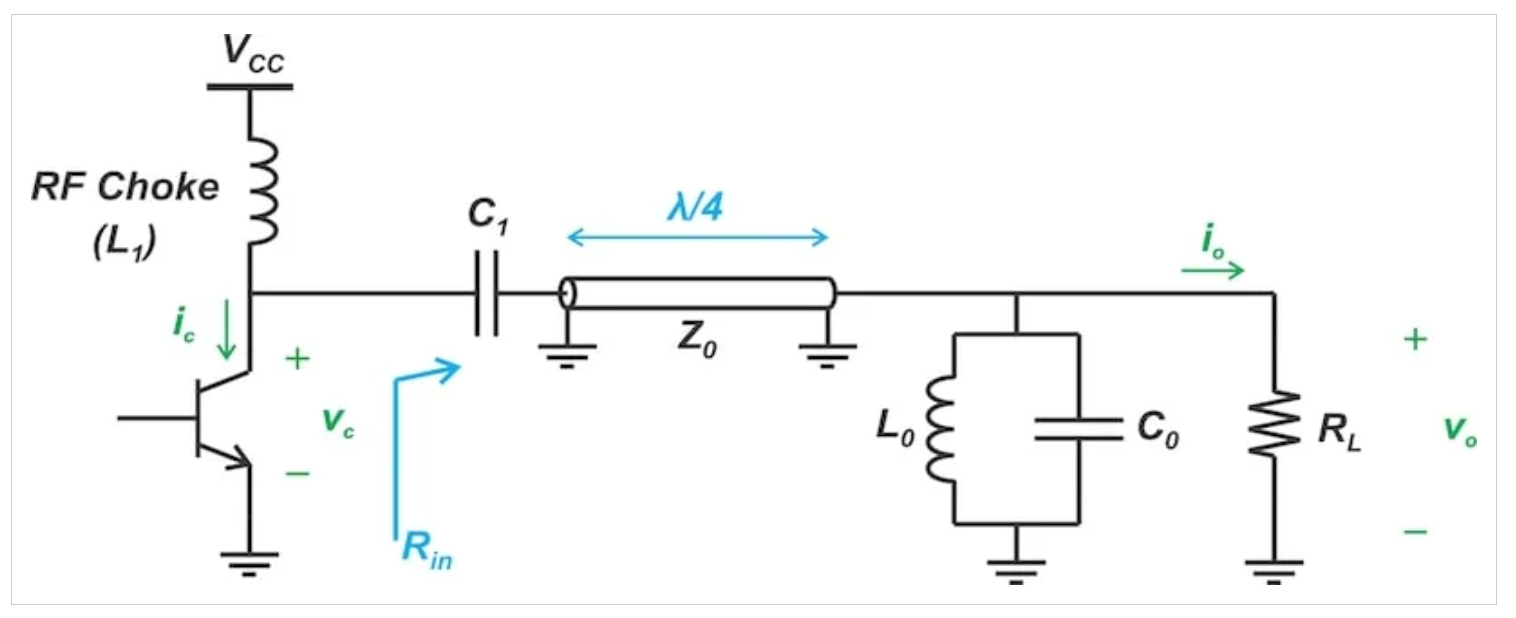
图1 带有四分之一波长传输线的F类放大器

要了解这个电路是如何工作的，我们首先需要了解以下内容：

近似方波所需的谐波分量。

四分之一波长和半波长传输线的阻抗变换。

我们将在本文的下两节讨论这些概念。之后，我们将检查理想传输线峰值放大器的波形并计算其效率。最后，我们将通过一个设计示例来结束本文。

方波的谐波含量

图2显示了峰间振幅为a、周期为T的方波。

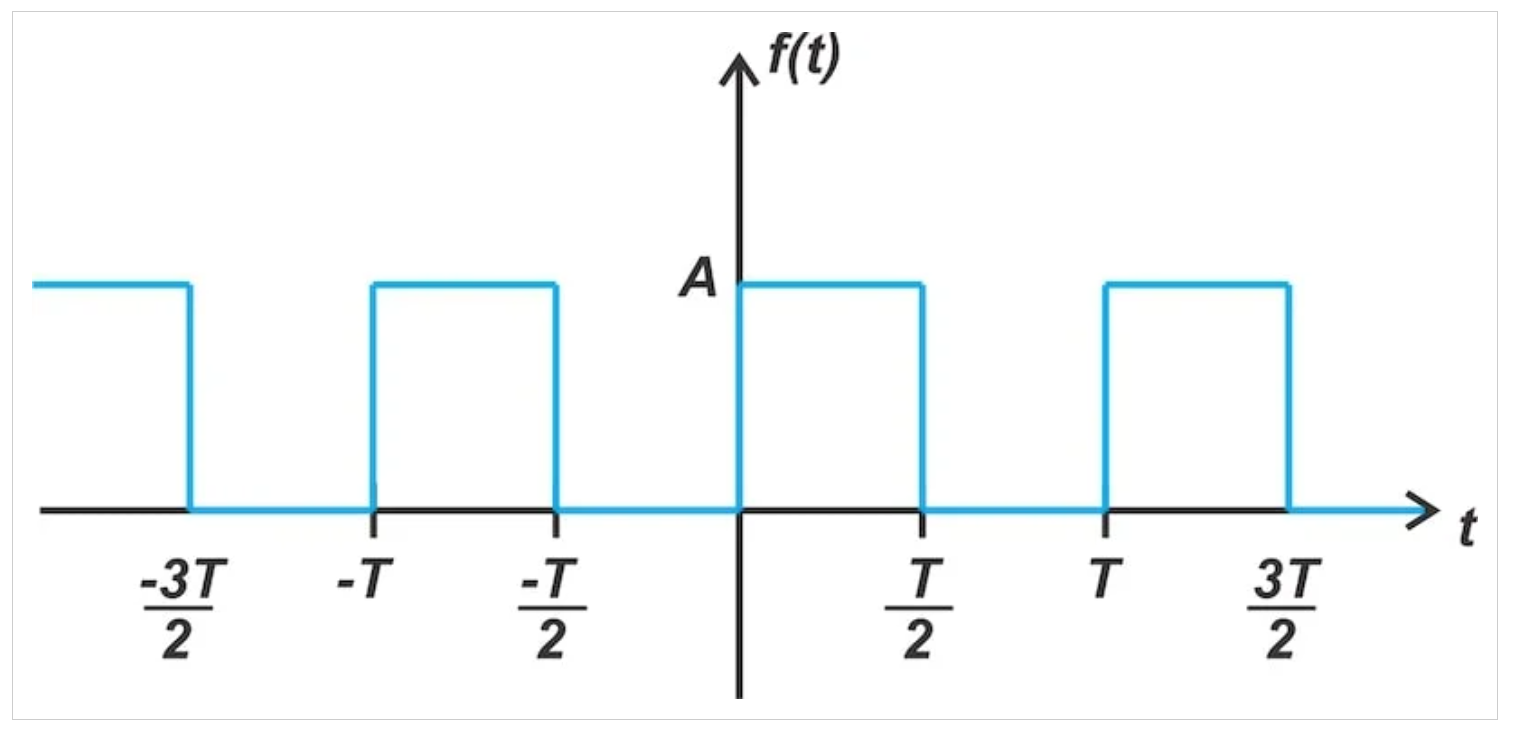
图2 峰间振幅为A的方波

通过采用傅里叶级数表示，可以将上述波形分解为其频率分量：

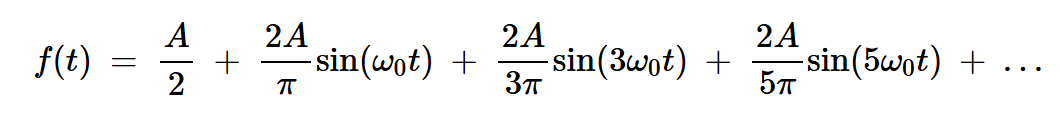
方程式1

从方程1中，我们可以看到方波是奇数谐波频率下的无限系列正弦波。我们知道，要在波形中添加给定的谐波分量，我们需要一个调谐到该谐波的谐振电路。因此，接近方波需要一种模拟无限阵列谐振器的结构。

图1中的电路通过使用与负载串联的四分之一波长线来实现这一点。本文的下一节将解释这是如何以及为什么起作用的。

四分之一波长和半波长线的阻抗变换

无损四分之一波长线的输入阻抗由下式给出：

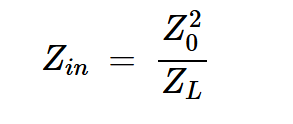
方程式2

解释：

Z0是线路的特性阻抗

ZL是负载阻抗。

我们在上面看到，四分之一波长线的输入阻抗与负载阻抗成反比。在传输线峰值放大器的情况下，我们有一条四分之一波长的传输线被短路端接。根据方程式2，在这种线路的输入端看到的阻抗是开路。

现在我们已经讨论了输入阻抗，下一步是检查收集器在不同谐波频率下看到的负载阻抗：

基频。

甚至谐波频率。

奇数谐波频率。

我们将从基频开始。

基频下的负载阻抗

在图1中，L0-C0油箱被调谐到基频。在该频率下，它充当开路，导致四分之一波长线在RL处终止。应用方程2，传输线在基频下的输入阻抗（如集电极所见）是一个纯电阻值，由下式给出：

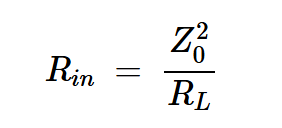
方程式3

如果线路的特性阻抗等于负载阻抗（Z0=RL），则我们得到Rin=RL。

偶谐波负载阻抗

在图1中，L0-C0油箱在所有谐波下都将输出节点接地短路。在偶次谐波时，线路的长度变为信号半波长的整数倍。例如，在二次谐波处，该线是半波长线。在四次谐波处，该线是一条全波长线。

当线路的长度是半波长的整数倍时，线路输入端的阻抗等于其负载阻抗（Zin=ZL）。为了理解这一点，我们首先注意到半波长线可以分成两条四分之一波长线。

然后，我们可以使用方程2来证明无损半波长传输线的输入阻抗等于其负载阻抗（ZL），而与线路的特性阻抗无关。因此，在偶次谐波时，集电极看到连接到线路右端的阻抗，这是短路。

奇数谐波的负载阻抗

在奇数谐波频率下，该线实际上变成了四分之一波长的奇数倍。因此，在这些频率下，输出端的短路转化为集电极的开路。要理解这一点，请参见方程式1。

最终结果是，负载网络等效于无限数量的并联谐振电路。如图3所示，该图显示了Z0=RL在不同谐波下的等效输入阻抗。

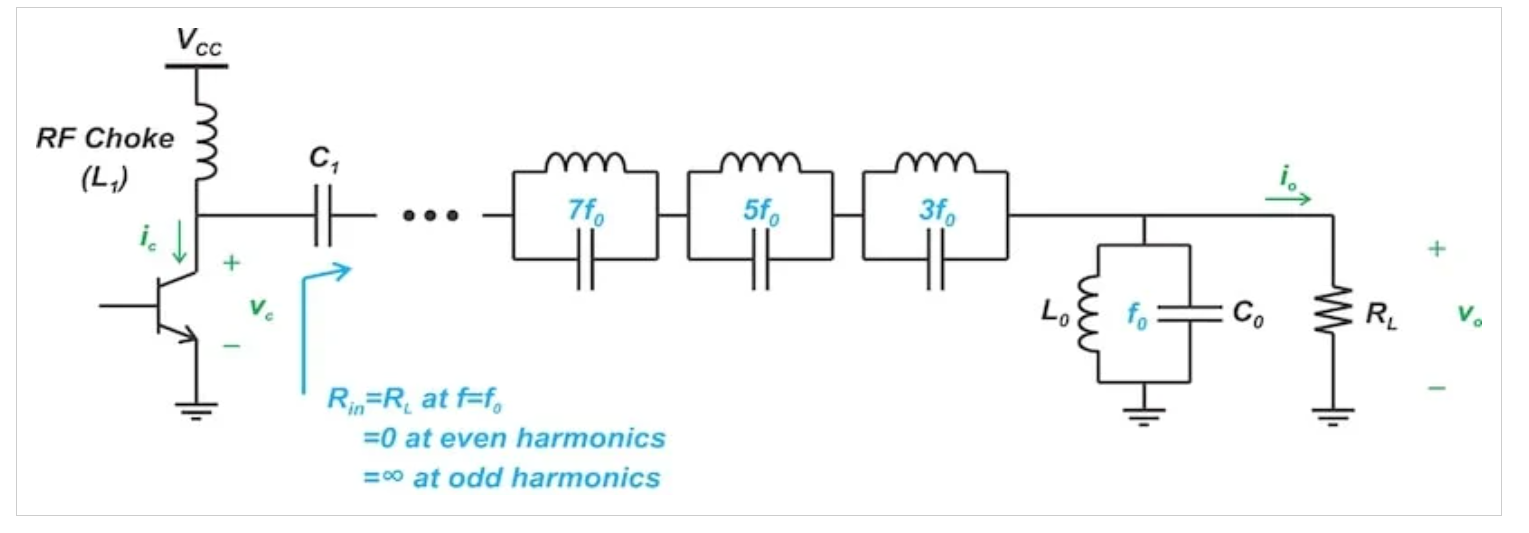
图3 对于Z0=RL，传输线峰值放大器在不同谐波下的等效输入阻抗

在偶次谐波短路端接和奇次谐波开路端接的情况下，集电极电压波形被迫仅包括基频和奇次和谐波。结果，方波集电极电压是可能的。

理想传输线峰值放大器的波形

图4显示了在传输线峰值放大器中观察到的典型波形。

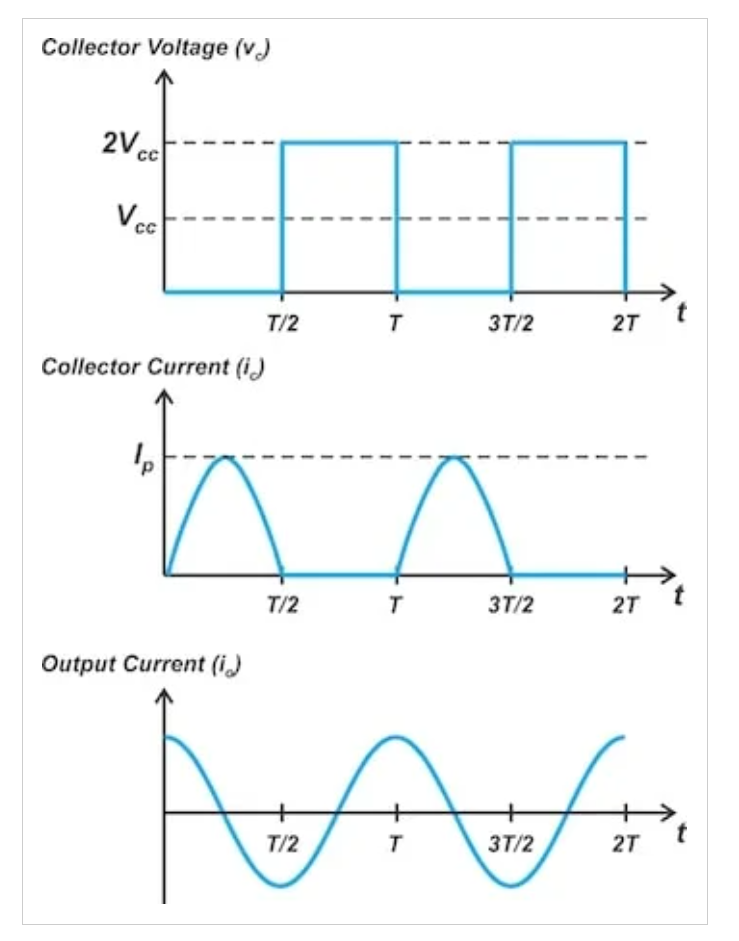
图4 传输线峰值放大器中的集电极电压（顶部）、集电极电流（中部）和负载电流（底部）

施加到晶体管输入端的信号是一个偏移正弦波，它将晶体管偏置在器件的导通电压（对应于180度的导通角）。在导通半周期期间，集电极电压（vc）为零

我们知道风险投资是方波。由于理想的射频扼流圈两端没有直流电压降，我们还知道vc的直流分量等于Vcc。在导通半周期的占空比为50%且vc=0的情况下，我们可以得出结论，在截止半周期的集电极电压应等于2Vcc。

方波电压具有所有奇次谐波分量。然而，由于负载网络对基波以上的奇次谐波呈现开路，因此它仅在基频下传导电流。因此，输出电流（io）在基频下是正弦波。

这也意味着晶体管的电流在导通半周期内是正弦曲线。由于在OFF半周期期间集电极电流为零，因此结果为半正弦波集电极电流。

总结一下：

集电极电压被奇次谐波的高阻抗整形为方波。

集电极电流是半波整流正弦曲线。

在理想情况下，电流和电压波形与D类放大器的波形相同。

最后，对上述波形进行目视检查，可以发现vc和io的基波分量之间存在相位差。这是因为电流（或电压）波在通过四分之一波长传输线时会经历90度的相位差。因此，vc的基本成分领先io 90度。

计算放大器的效率

假设集电极电压是一个方波，其峰间电压摆动为2Vcc。从方波的傅里叶级数表示（方程1）中，我们知道vc基波分量的振幅为：

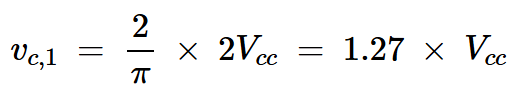
方程式4

当传输线连接到匹配的负载时，电压信号沿传输线长度的幅度是恒定的。因此，对于匹配的终端（Z0=RL），我们可以得出结论，输出电压的幅度也是vo=（4/π）Vcc。请注意，vo的幅度大于Vcc，Vcc是B类放大器中观察到的摆动幅度的典型极限。这类似于在三次谐波峰值放大器中观察到的行为。

功率放大器的效率公式为η=PL/Pcc。如果我们知道输出电压，我们可以计算出输送到负载的平均功率，如下所示：

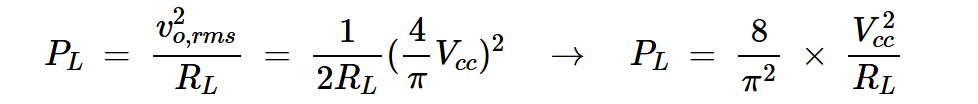
方程式5

为了计算电源功率，我们找到从电源中提取的平均电流（图3中中间曲线的平均值），并将其乘以电源电压。然后，我们使用傅里叶级数表示法将半波整流集电极电流表示为其频率分量之和：

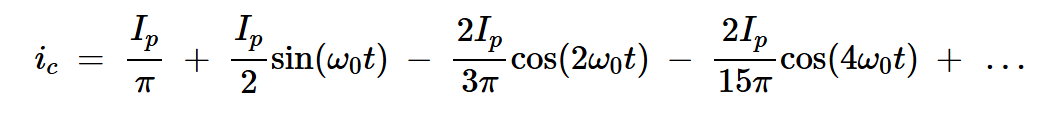
方程式6

假设平均集电极电流为Ip/π，电源的功率输出计算如下：

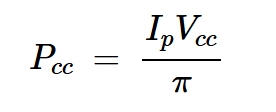
方程式7

我们可以使用方程式5和7来计算放大器的效率，但只有在建立Ip和Vcc之间的关系后才能使用。为此，我们注意到ic基波分量的振幅为Ip/2。该电流流入负载（RL），并产生基本电压幅度vo=（4/π）Vcc。因此，我们有：

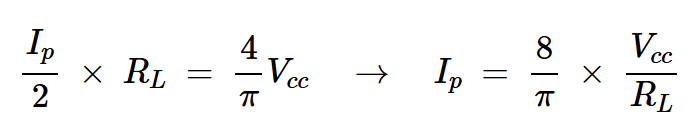
方程式8

我们现在可以将方程式7和8结合起来，得出从电源中提取的功率：

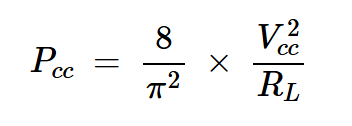
方程式9

比较方程式5和9，我们可以看到负载功率和电源功率是相同的。因此，放大器的理论效率为100%。

请注意，这是一个简化的分析——我们假设晶体管作为一个理想的开关，具有零导通电阻、无限截止电阻和无输出电容。我们还假设切换动作是瞬时且无损的。

使用传输线进行阻抗匹配

我们可以设计传输线，使外部负载与集电极阻抗相匹配。这使我们能够在基频下最大限度地提高输出功率。

为了计算这种情况下的输出功率，我们注意到，传输到无损线路输入端的平均功率等于传输到其终端的平均功率。应用方程式4，得出输出功率为：

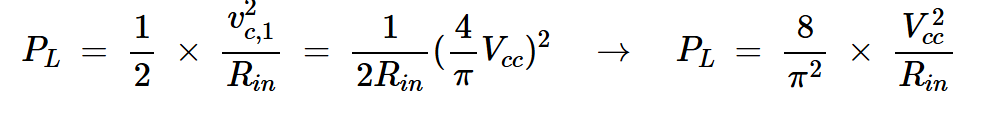
方程式10

其中Rin是线路的输入阻抗。

为了帮助巩固这些概念，让我们通过一个设计示例。

示例：设计传输线峰值放大器

假设我们正在设计一个如图1所示的F类放大器。对于该放大器，线路的特性阻抗为Z0=50Ω，电源电压为Vcc=30V。确定以下内容：

我们应该使用负载阻抗（RL）向负载提供PL=7.3 W的功率。

晶体管必须承受的最大电流和电压。

第一步是通过应用方程式10来找到线路所需的输入阻抗：

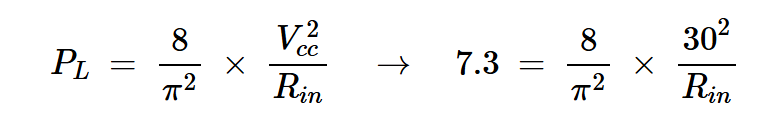
方程式11

求解输入阻抗得到Rin≈100Ω。现在我们有了Rin的值，我们使用四分之一波长线的输入阻抗方程来计算RL：

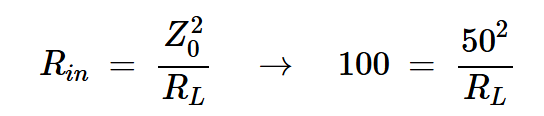
方程式12

其结果为RL=25Ω

从图4中可以看出，最大集电极电压为2Vcc=60 V。这只留下了最大集电极电流，我们在方程8中使用Rin而不是RL找到了这一点：

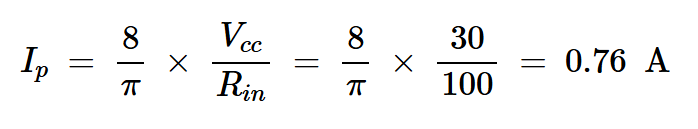
方程式13

总结

传输线峰值F类放大器使用由四分之一波长传输线和并联谐振电路组成的负载网络。集电极电压包括基波和奇次谐波分量，而集电极电流包括基波分量和偶次谐波分量。因此，仅在基频下产生电力，从而实现了100%的理想效率。

如前所述，这种放大器广泛应用于VHF和UHF FM无线电发射机。然而，我们必须记住，由于所需的线路长度，将传输线实现到F类放大器IC中可能具有挑战性。即使在2.4GHz的频率下，四分之一波长传输线的长度也超过3cm。