ADC INL误差——最佳拟合线、总未调整误差、绝对和相对精度

了解更多关于模数转换器（ADC）中的积分非线性（INL）的信息，如最佳拟合线INL定义、绝对精度、相对精度和总未调整误差（TUE）。

积分非线性（INL）是一个重要的规范，它使我们能够表征A/D（模数）转换器的静态线性性能。INL误差量化了实际传递函数的转变点与理想值的偏差，理想值是从参考直线获得的。然而，不同的INL定义使用不同的参考线。

之前，我们研究了其中一些定义，比如基于端点的定义。作为复习，最常见的INL定义的参考线是穿过第一个和最后一个代码转换的线（图1中穿过点a和B的线）。

参考线INL定义示例。

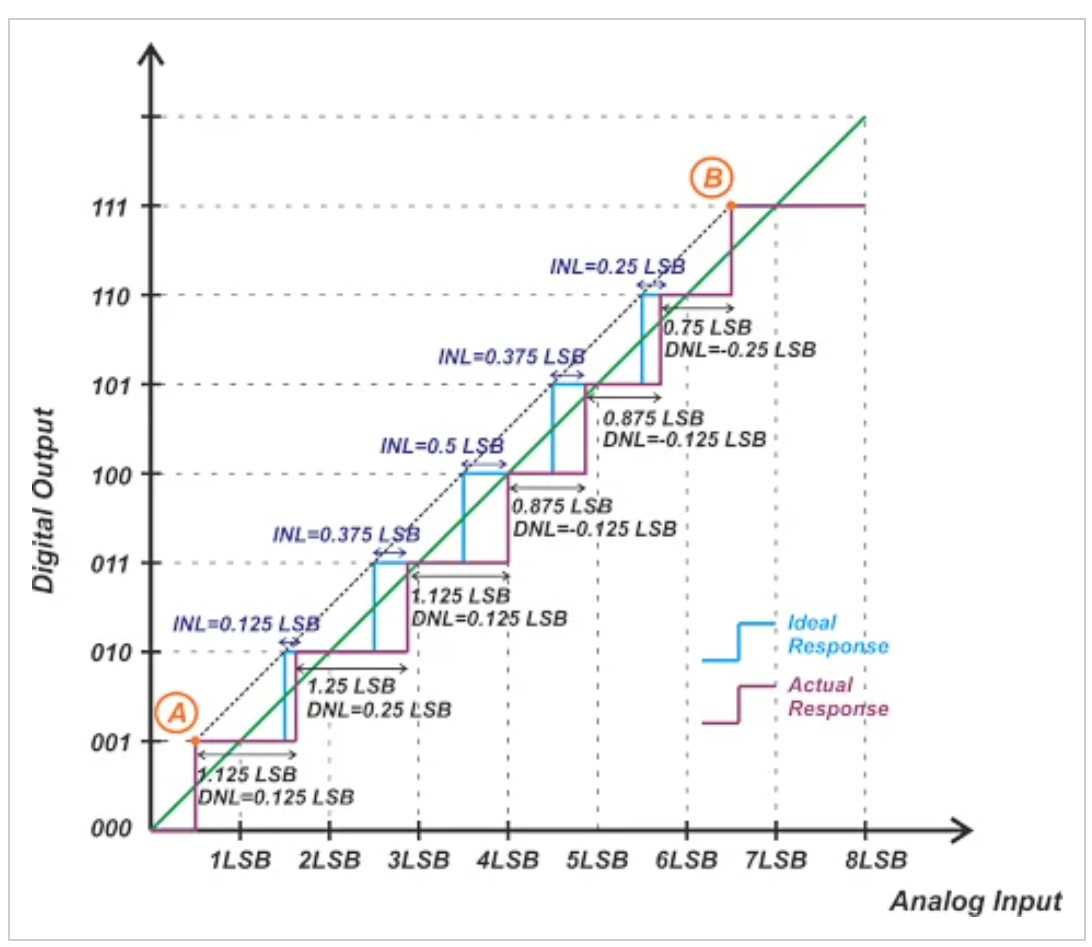
图1。参考线INL定义示例。

上述INL定义被归类为端点方法，因为它只使用第一个和最后一个代码来推导参考线。在本文中，我们将介绍另一种定义INL误差的方法，即最佳拟合线方法。在这种情况下，使用穿过所有代码的直线拟合作为参考线。

过渡最佳拟合INL——端点法与最佳拟合法

无论使用端点还是最佳拟合方法，ADC的静态传输特性都可以根据码中心或转换点来定义。基于过渡的最佳拟合INL定义的参考线是最能代表特征曲线所有过渡点的直线。让我们考虑图1中的非理想响应，如图2所示。

非理想响应示例。

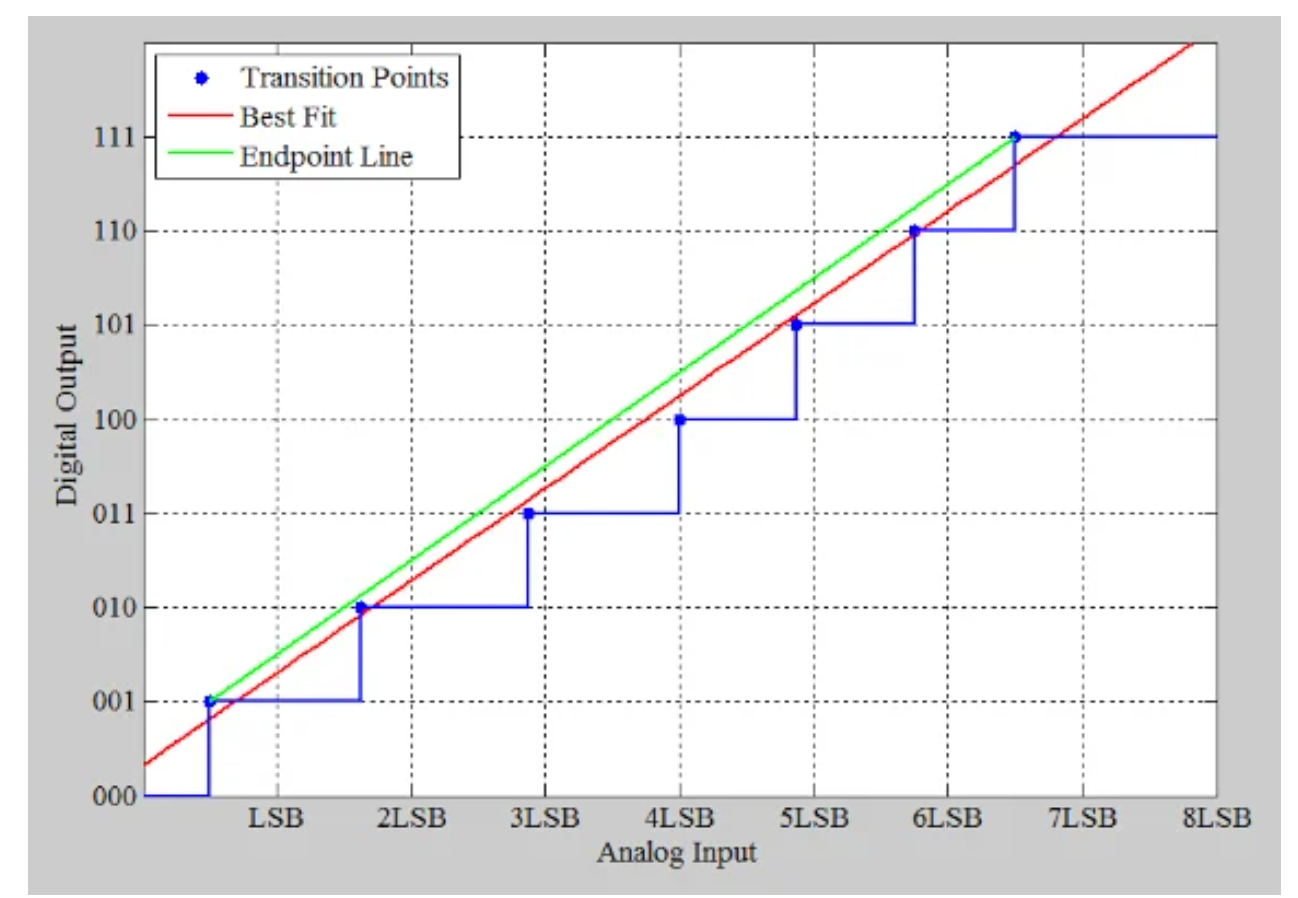
图2:非理想响应示例。

在图2中，点表示特征曲线的过渡点，绿线是穿过第一个和最后一个过渡点的端点线。显然，一条直线不能穿过所有这些过渡点。然而，我们可以找到“最适合”我们数据点的直线（图中的红线）。最小二乘法用于寻找最佳拟合线。

最小二乘法是一种统计方法，通过最小化直线上各点的偏移（或“残差”）之和，将直线拟合到数据中。最小二乘法中涉及的计算是乏味的，通常使用电子表格或计算机程序来进行这些计算。

例如，如图2所示，计算过渡点与最佳拟合线的偏差会得到以下INL图。

计算过渡点与最佳拟合线偏差的INL图示例。

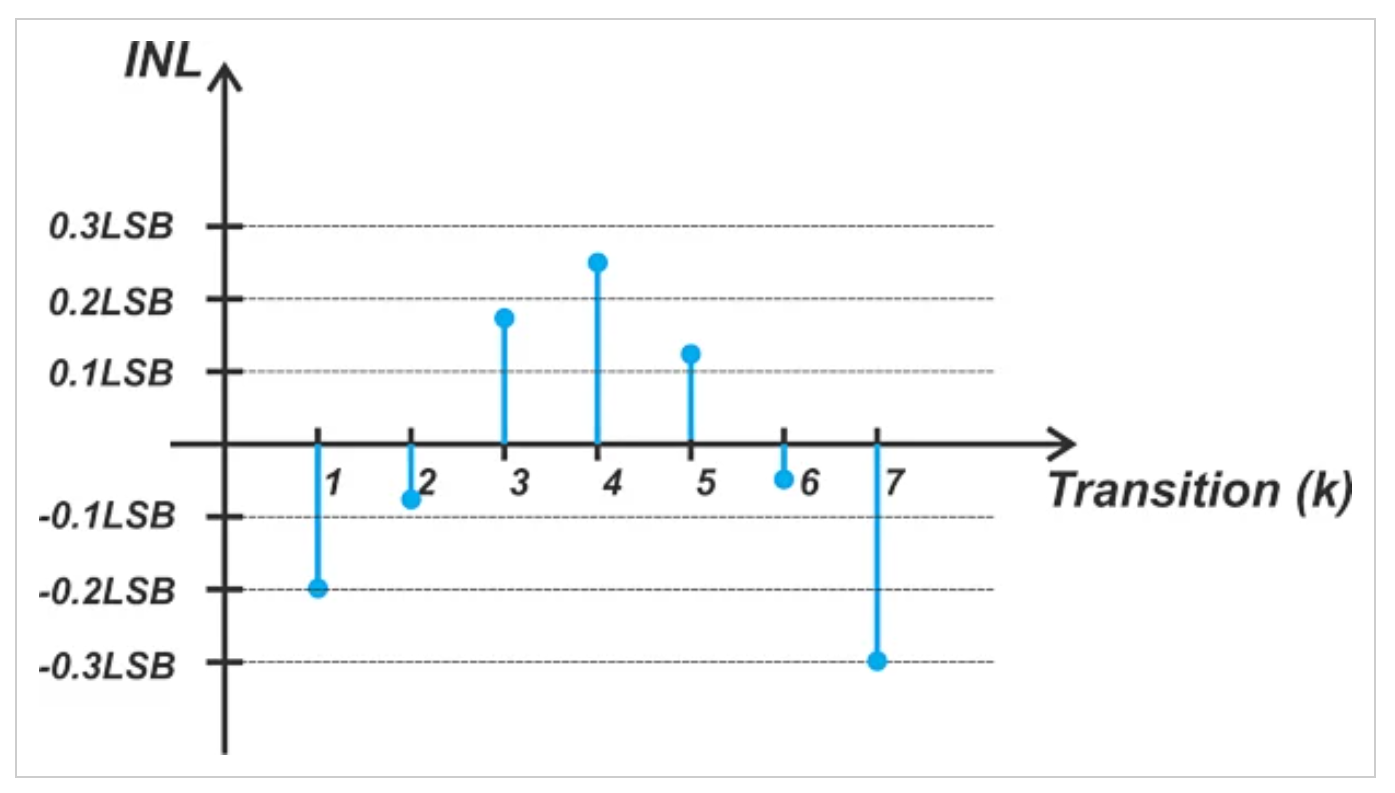
图3。计算过渡点与最佳拟合线偏差的INL图示例。

对于这个假设的ADC，应用端点方法会导致最大INL误差为+0.5个最低有效位（LSB），如图1所示。然而，使用最佳拟合方法，INL误差的绝对值小于0.3 LSB，几乎是端点方法的一半。图4应该可以帮助您更好地可视化最佳拟合方法如何使给定的特征曲线看起来更线性。

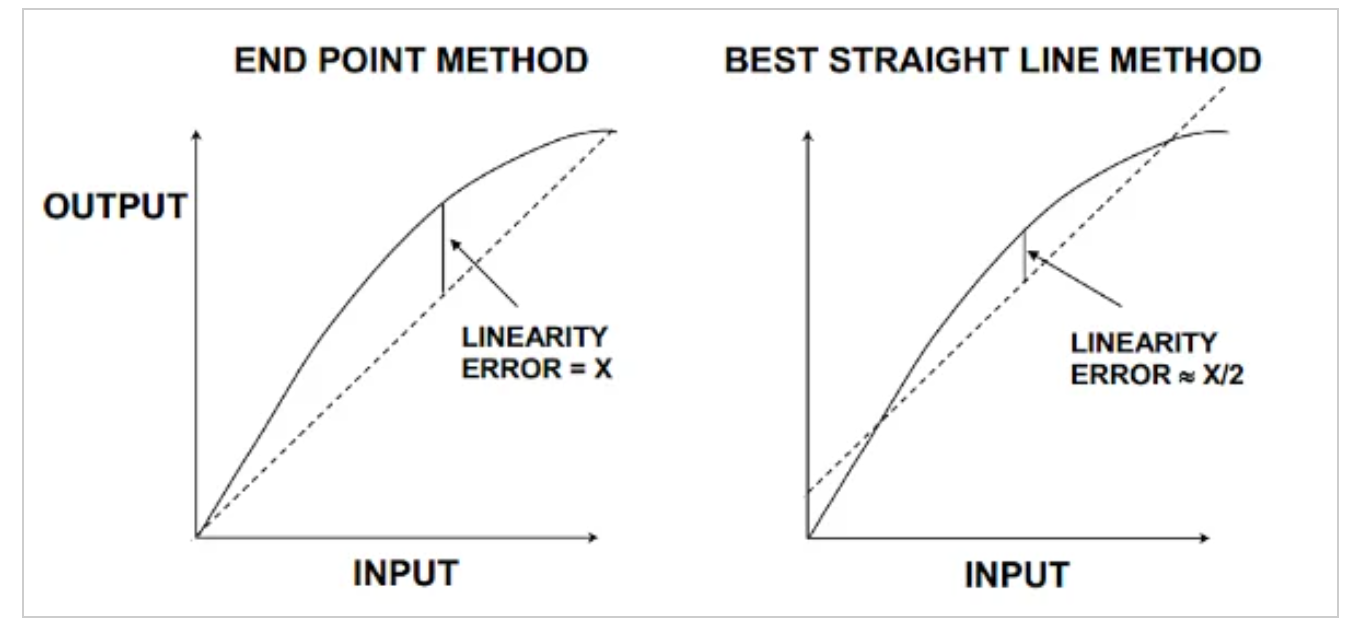
图4。示例显示了端点法（左）和最佳直线法（右）。图片由Analog Devices提供[PDF]

在图4中，实线表示非线性ADC响应。如您所见，最佳拟合方法固有地选择了一条参考线，该参考线使最大INL误差最小化，并倾向于隐藏线性性能的细节。因此，在分析测量系统的误差预算时，最佳拟合方法似乎并不真正有用。这是因为，对于误差预算分析，我们需要计算与理想传递特性的偏差，而不是与某种任意的“最佳拟合”的偏差

虽然端点方法更适合测量和控制应用，但最佳拟合方法可以更好地预测交流应用中的失真。然而，即使对于交流应用，我们通常也更喜欢使用谐波失真和无杂散动态范围（SFDR）等规范，因为这些指标可以表征系统的动态线性。

因此，很少需要使用最合适的INL规范。您需要熟悉它，因为您可能偶尔会遇到使用最佳拟合方法表征的设备。

代码中心最适合INL

为了完整起见，下面还显示了基于代码中心的INL定义。

基于代码中心的INL示例

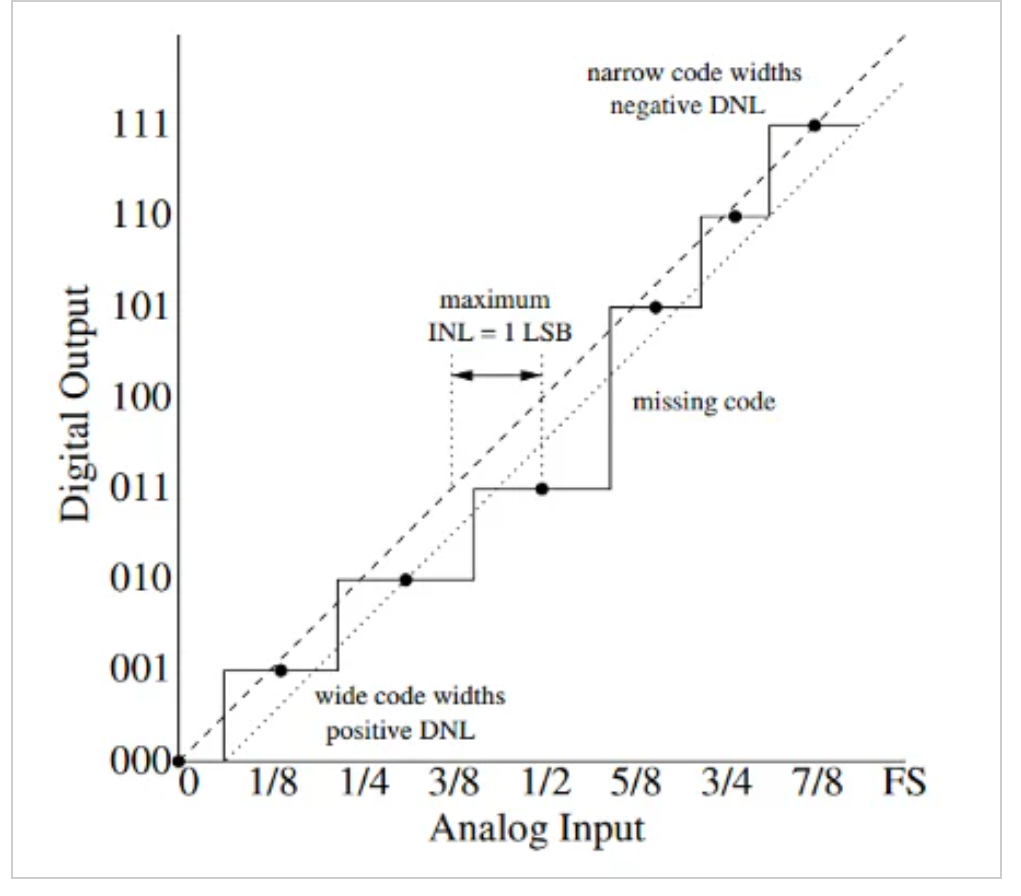
图5。基于代码中心的INL示例。图片由K.Lundberg提供[PDF]

在这个图中，虚线是ADC的线性模型，虚线是适合实际代码中心的线。INL定义为代码中心与参考线的距离。对于端点方法，参照线是虚线。然而，对于最佳拟合方法，参考线是虚线。同样，最佳拟合方法本质上隐藏了系统的非线性，并且可以产生比端点方法小得多的INL误差。

现在我们已经熟悉了INL规范，我们可以讨论如何定义ADC的精度。在ADC的背景下，精度实际上并不是一个定义良好的参数，我们稍后会讨论一些不一致之处。“绝对精度”、“相对精度”和“总未调整误差”是描述ADC中传递函数精度的三种常见方法。

ADC绝对精度

本TI文件将ADC在给定代码下的“绝对精度”定义为在理想代码中心的实际响应中产生特定代码的模拟输入之间的最大差值。图6（转载自我上面提到的文章）以图形方式最好地说明了这一点。

显示ADC绝对精度的图。

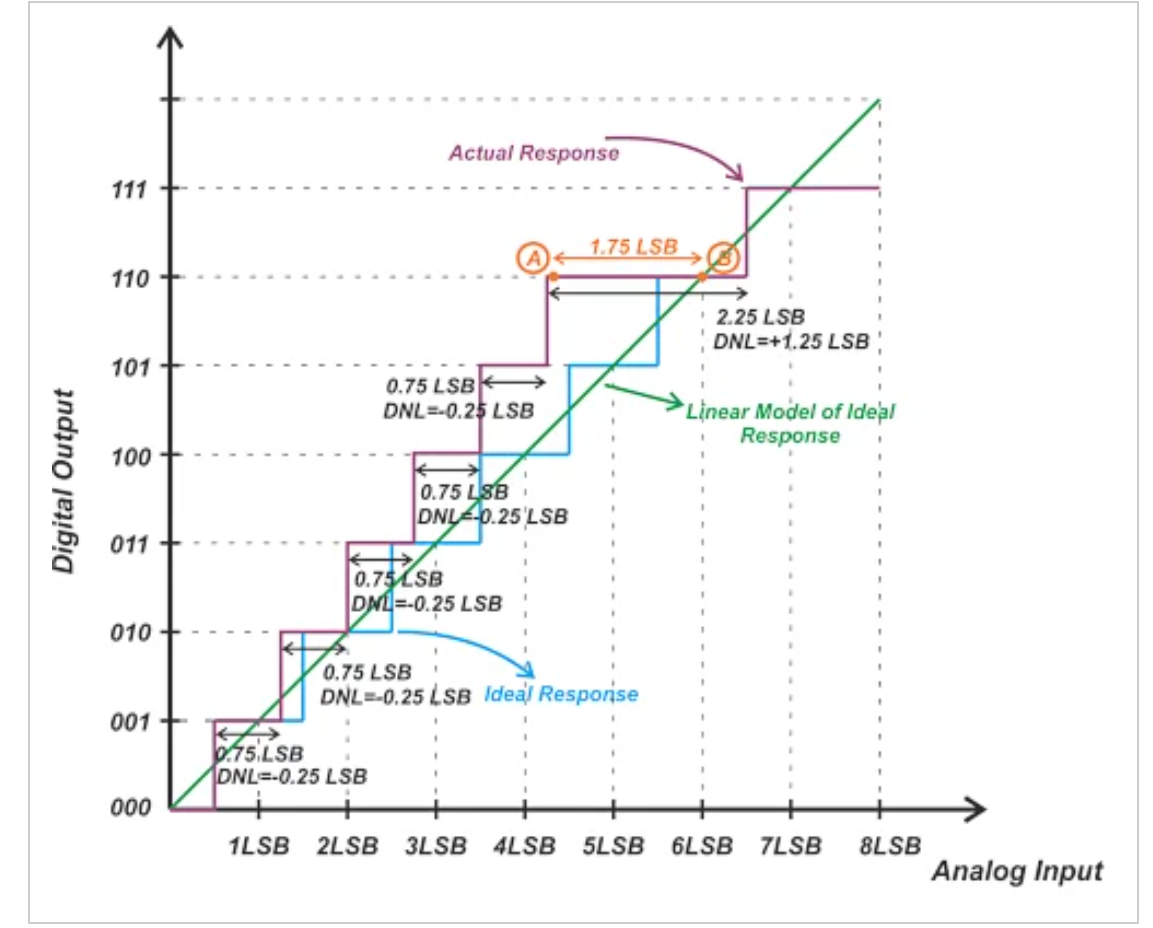
图6。显示ADC绝对精度的图。

在这个例子中，4.25 LSB的模拟输入（对应于点A）是产生代码110的最小值。代码110的模拟等效值是6个LSB。这意味着，对于4.25个LSB的输入，ADC输出6个LSB，导致1.75个LSB的绝对精度误差。如您所见，可以通过计算点A和理想代码中心（点B）之间的差值来发现此错误。图7显示了应用此精度定义的另一个示例。

应用绝对精度的另一个例子。

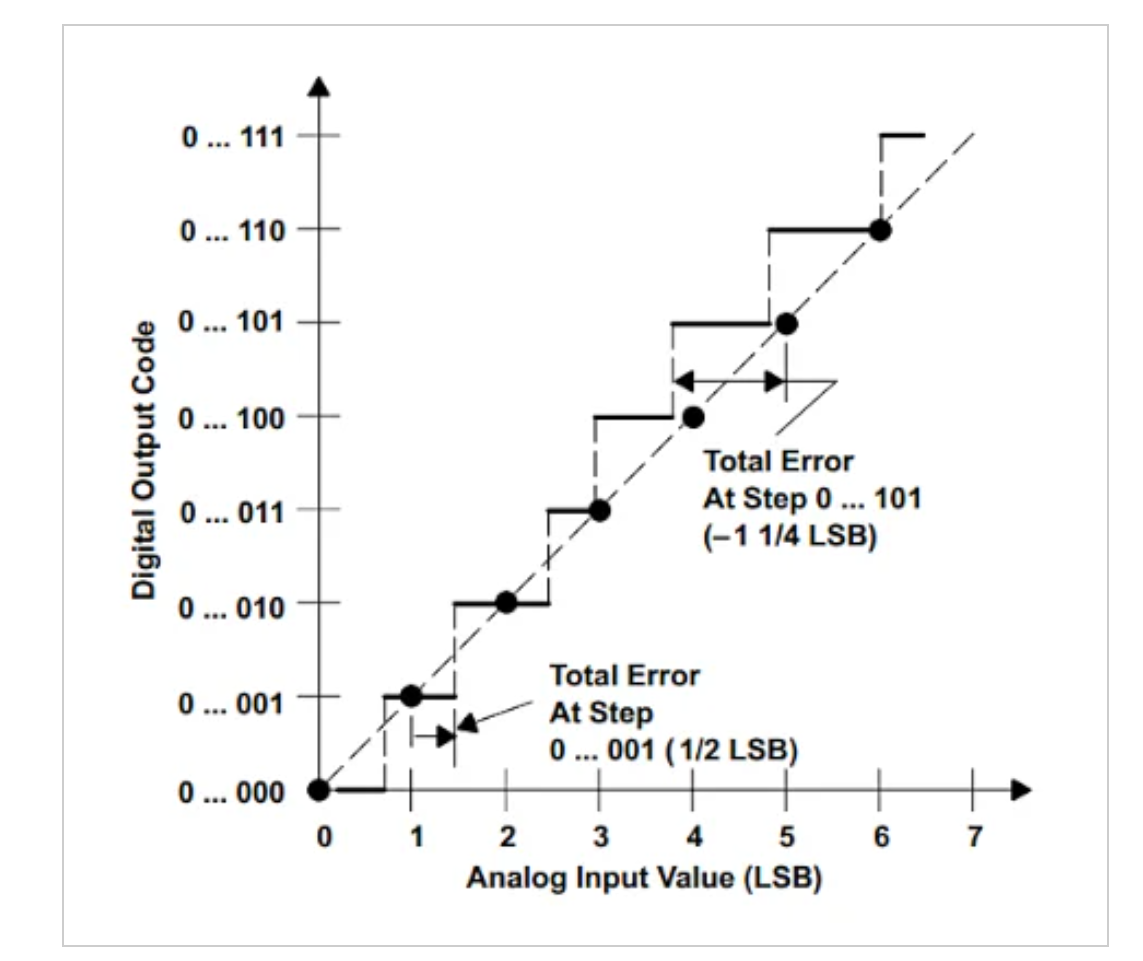
图7。应用绝对精度的另一个例子。图片由TI提供[PDF]

根据上述“绝对精度”定义，包括四种不同的误差源，即偏移误差、增益误差、INL误差和量化误差。然而，请记住，有时某些参考文献中提供的绝对精度定义不包括量化误差。例如，流行的教科书《模拟集成电路设计》将绝对精度定义为预期和实际传输响应之间的差异。该书进一步阐述了绝对精度包括偏移、增益和线性误差。

此外，《数据转换手册》一书也没有包括量化误差，并将绝对精度定义为实际和理想码中心之间的差异。例如，如果5V±1.2 mV范围内的值在理想响应中产生给定代码，而实际转换器在4.997 V至4.999 V的输入中产生该代码，则绝对误差为：

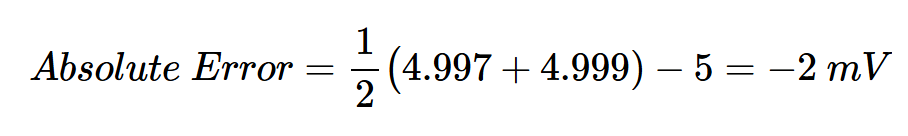
该定义类似于基于代码中心的INL定义；然而，不同之处在于，它在不消除偏移和增益误差的情况下计算误差。

ADC相对精度

“相对精度”是最大INL误差的另一个术语。因此，相对精度表示ADC在校准其偏移和增益误差后的精度。

ADC精度——总未调整误差（TUE）

TUE是表示ADC总精度的另一种方式。TUE也是偏移、增益和INL误差的组合效应。然而，它并不是这些误差的总和。最大TUE通常计算为偏移、增益和INL误差最大值的均方根（RSS）：

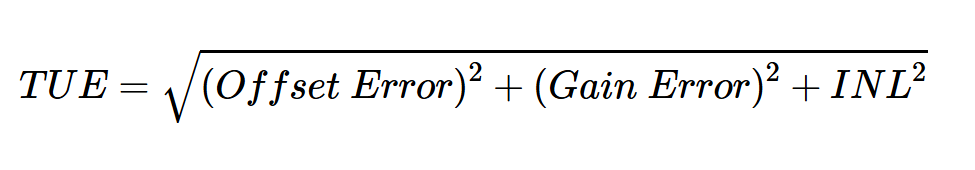
TUE还可以用来表示整个采集系统的精度。在这种情况下，还包括来自其他块（如输入驱动器、电压基准等）的偏移和增益误差。

ADC INL错误的关键要点

INL误差量化了实际传递函数与理想响应的偏差。不同的INL定义使用不同的参考线来定义理想响应。INL定义可分为端点法和最佳拟合法。

端点方法使用第一个和最后一个代码来推导参考线，而最佳拟合方法使用最佳拟合线作为其参考。

无论使用端点还是最佳拟合方法，ADC的静态传输特性都可以根据码中心或转换点来定义（用于INL计算）。

ADC的精度通常用三种规格表示：绝对精度、相对精度和TUE。