利用噪声系数度量分析射频电路中的噪声
关于射频模拟设计中的噪声分析,通过示例了解噪声系数度量,包括本规范的关键方面。
本文引用地址:https://www.eepw.com.cn/article/202409/462816.htm除了一些特定的应用,例如,当需要抖动效果时,噪声通常是一种不想要的现象。科学家和工程师已经表征了不同电路元件产生的噪声,并开发了可用于分析电路噪声性能的方法。在模拟电路设计中,我们通常将噪声效应建模为输入参考噪声电压和电流源。然而,在射频(RF)设计中,噪声系数度量可以是表征电路噪声性能的更有用的方法。
在本文中,我们将介绍噪声系数度量,强调该规范的一些微妙之处,最后看一个例子来澄清所讨论的概念。
射频模拟设计中的噪声分析
我们通常用串联电压源来模拟电路中所有噪声源的影响 (¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯v2n,input)
以及并联电流源 (¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯i2n,input),如图1所示。
串联电压源和并联电流源电路中噪声源的影响。
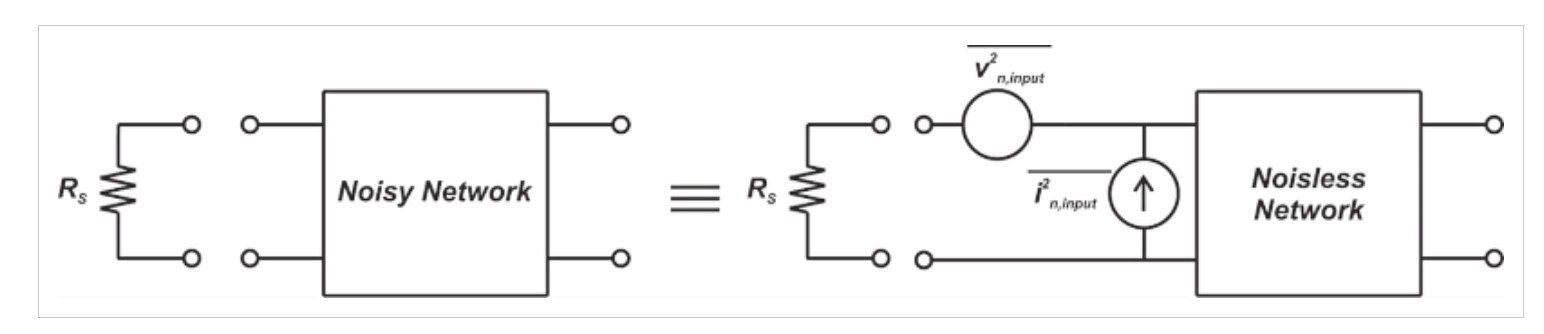
图1。串联电压源和并联电流源电路中噪声源的影响。
在图1中,“无噪声网络”与“有噪声网络”相同,除了其组件(电阻器、晶体管等)被假设为无噪声。通过将两个电路的输出噪声相等,我们可以找到输入参考噪声电压和电流源的值。对于任何源阻抗(RS),这两个输入发生器对于正确建模线性双端口网络的噪声是足够和必要的。
使用OP27运算放大器示例了解源阻抗
在射频设计,特别是离散射频设计中,我们通常更喜欢使用噪声系数概念,而不是噪声电压和电流源模型。然而,上述模型可以帮助我们更好地理解电子电路中的噪声行为和噪声系数度量的微妙之处。
一个关键的观察结果是,电路的输出噪声取决于前级的输出阻抗(或源阻抗,RS)。这可以通过考虑RS=0和RS趋于无穷大(RS→∞)的极端情况来理解,
RS = 0, ¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯i2n,input
是短路,对输出噪声没有影响。
另一方面如果RS趋于无穷大,
v2n,input
不能产生输出噪声。图2显示了源极电阻(R)对实际运算放大器(OP27)配置的影响。
源极电阻对OP27运算放大器配置的影响。
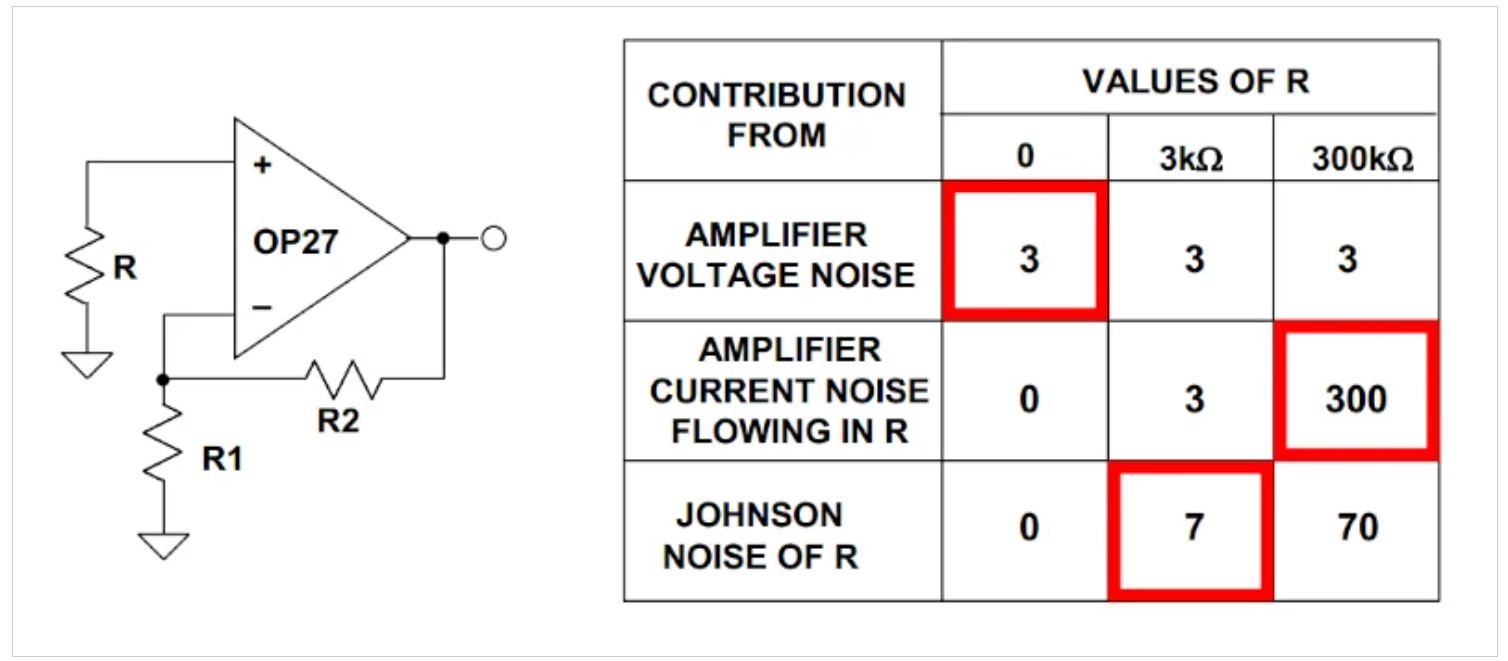
图2:源极电阻对OP27运算放大器配置的影响。图片由ADI公司提供
OP27的电压噪声为
3nV√Hz
在上述示例中,仅考虑了来自源阻抗(R)和运算放大器的噪声。对于R=0,运算放大器噪声电流源短路,整体输入参考噪声由运算放大器的电压噪声决定
1pA√Hz
当我们将源电阻增加到R=3kΩ和300kΩ时,运算放大器噪声电流源预计会流过运算放大器的源阻抗和输入阻抗。然而,由于运算放大器的输入阻抗在几个MΩ的范围内,噪声电流仍然主要通过源阻抗流动。因此,对于R=3kΩ和300kΩ,噪声电流产生的等效噪声电压分别为
3nV√Hz 和 300 nV√Hz
对于R=3kΩ和300kΩ,运算放大器的噪声电压仍然会产生
3nV√Hz
因为这些电阻值与运算放大器输入阻抗相比相对较小。
图2中的表格还给出了所考虑的三个不同值的R热噪声。如图所示,主要噪声源(图2中红色矩形突出显示)以及电路的整体噪声性能随源阻抗而变化。在使用噪声系数度量时,这是一个需要记住的重要概念(稍后将讨论)。
对替代噪声度量的需求
输入参考噪声发生器模型不适合射频设计。例如,在计算RF增益级的输入参考噪声电流时,我们需要测量该级在感兴趣频率下的跨阻抗。这种测量在高频下非常具有挑战性。因此,人们希望找到另一种在高频下更容易测量的噪声性能指标。
此外,在许多射频系统中,我们对信号功率与噪声功率的比值(信噪比或信噪比)感兴趣。信噪比指定了信号的质量,并最终决定了我们的通信系统接收到的数字比特中有多少是错误的(系统的误码率)。
所需的信噪比取决于各种因素,例如:
调制方案
比特率
每比特能量
滤波器带宽
大多数数字通信系统需要至少10dB的信噪比。在执行解调的接收器系统的输出端测量信噪比。如图3所示,典型的接收器信号链由几个不同的块组成,如低噪声放大器(LNA)、混频器、滤波器和模数转换器(ADC)。
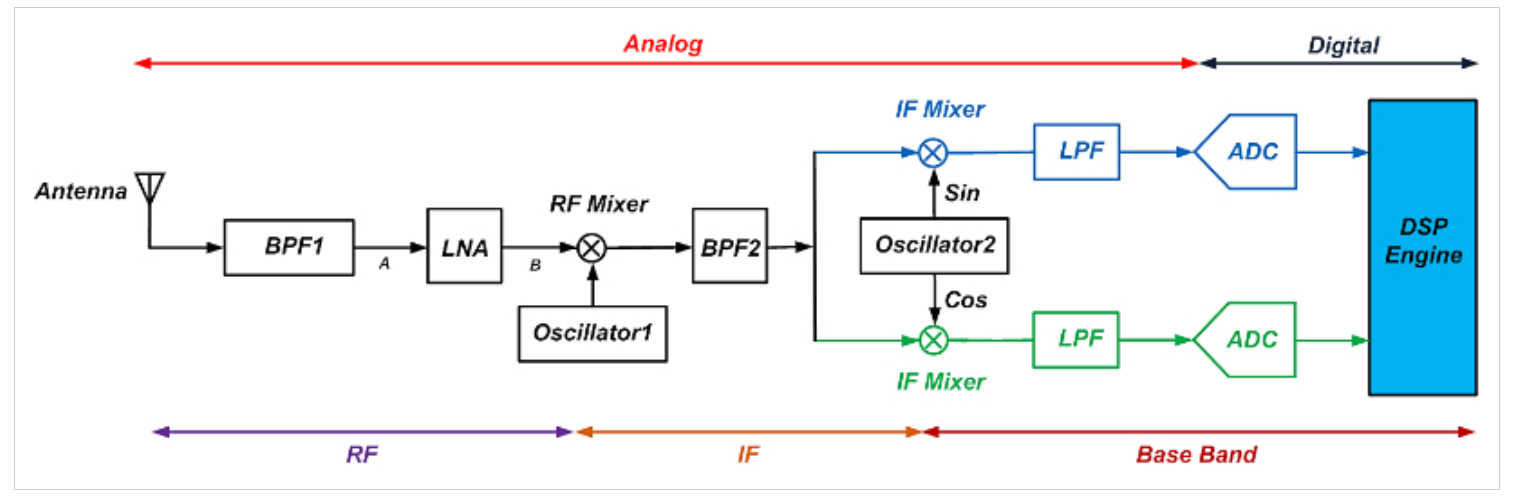
图3。示例接收机信号链框图。
射频工程师需要知道这些电路组件中的每一个是如何影响噪声性能的,以及信号在信号链中传播时信噪比是如何降低的。因此,与信噪比直接相关的噪声性能指标在射频设计中可能更有帮助。这就是噪声系数规范的突出之处,因为噪声系数在高频下更容易测量,并且直接基于信噪比规范定义。
噪声系数和噪声系数测量
电路的噪声系数(F)定义为输入端的信噪比与输出端的信信噪比之比:
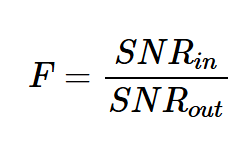
方程式1。
在上述方程中,噪声和信号功率量以线性项表示,而不是以分贝表示。以分贝表示的噪声系数称为噪声系数(NF):
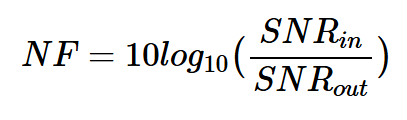
方程式2。
应当注意,一些参考文献没有做出这种区分,而是使用术语噪声系数来指代方程1和2。在这种情况下,我们应该从上下文中确定噪声系数是以分贝还是线性表示的。
对于无噪声电路,输入和输出信噪比相同,导致F=1和NF=0 dB。噪声系数是电路引起的信噪比劣化的直接度量。例如,如果电路输入端的信噪比为60dB,电路噪声系数为7dB,那么电路输出端的信信噪比是53dB。更精确地说,假设电路的输入噪声功率等于计算电路NF的参考噪声功率,则此陈述是有效的(我们将在即将发表的文章中对此进行详细讨论)。
其他噪声系数定义
使用一点代数,我们可以从方程1中推导出有用的替代表达式。如果我们用Si和So表示电路输入和输出端的信号功率,用Ni和No表示输入和输出的噪声功率,我们得到以下方程:
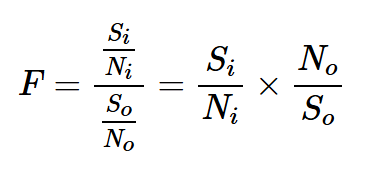
考虑到这一点,您可能会想知道,输出信号与输入信号有什么关系?由于这些是功率量,我们需要考虑电路的功率增益。在功率增益为G的情况下,我们得到So=GSi,这导致了方程3:
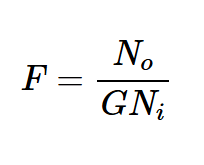
方程式3。
在方程式3中,No是输出端的总噪声。它包括电路内部噪声源的影响以及源阻抗(或前一级的输出阻抗)的噪声。Ni是源阻抗(RS)在电路输入端产生的噪声。根据方程式3,噪声因子是总输出噪声除以来自源电阻的输出噪声部分。
为了推导另一个表达式,让我们关注源阻抗No(源)产生的输出噪声部分,以及电路内内部噪声源No(添加)产生的部分。因此,我们得到:
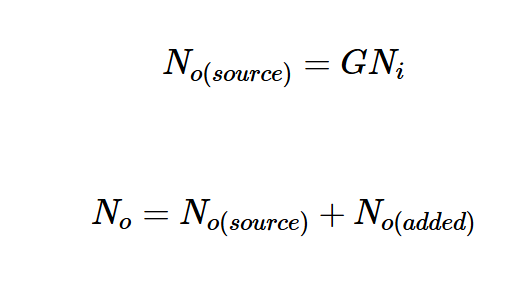
将这些方程代入方程3,得到方程4:
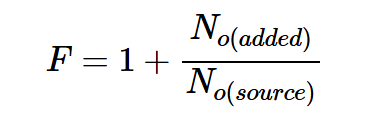
方程式4。
方程式4表明,我们获得的噪声系数值取决于连接到电路的源阻抗(RS)。在方程式4中,No(源)显然是RS的函数。然而,根据我们在上一节中的讨论,我们知道电路本身的噪声也是RS的函数,因此,必须指定已知源阻抗的噪声系数,通常为50Ω。
计算示例电路中的噪声系数
在这个例子中,我们将使用方程式1和4来计算以下电路的噪声系数(图4)。
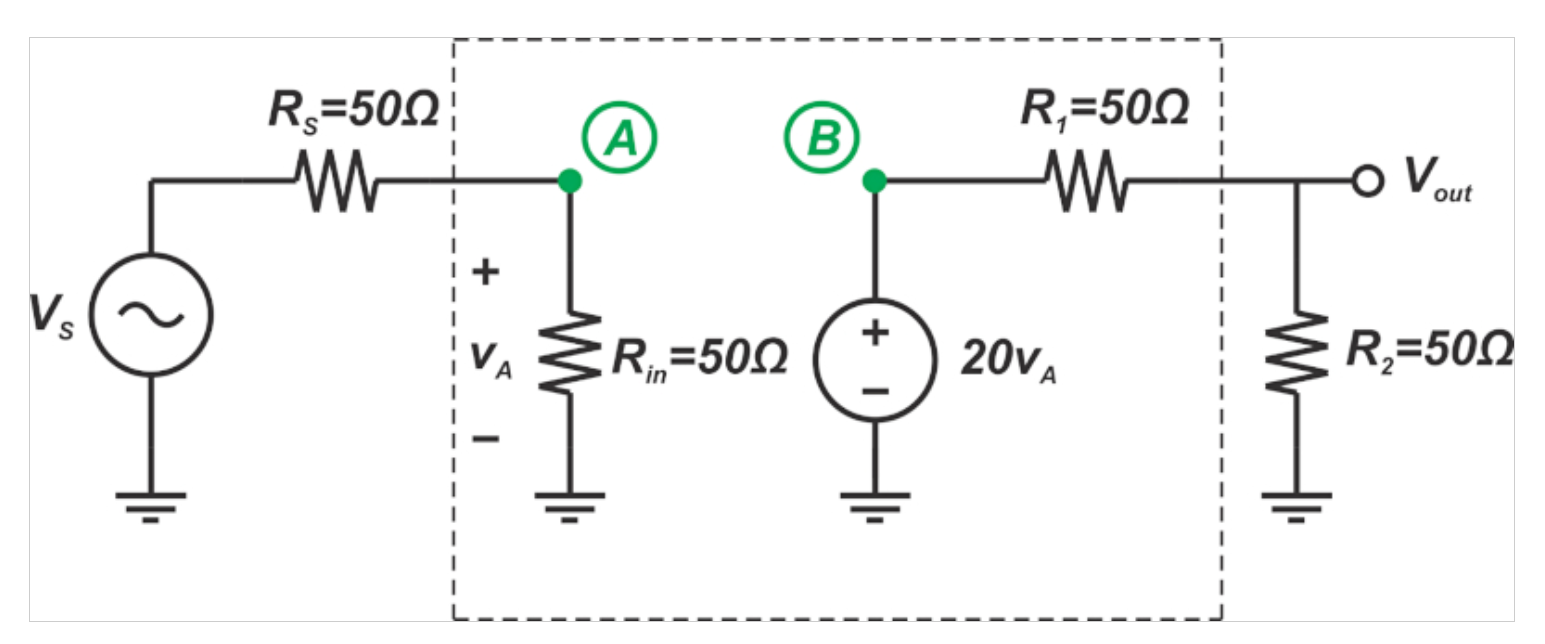
图4。示例电路。
我们假设输入电压的均方根值为VS,所有电阻值均为50Ω,系统的噪声带宽为Bn=1 MHz。
为了使用方程1,我们需要计算电路输入和输出处的信噪比。由于RS=Rin,电路输入端(节点A)的输入信号减半。因此,节点A处信号的RMS值为:
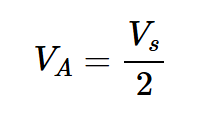
输入信号功率为:
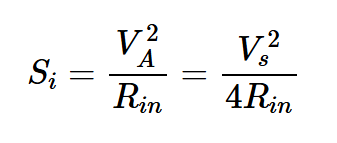
方程式5。
完成后,我们可能会问如何计算输入噪声。我们知道电阻R的均方根噪声电压
是V/√Hz
由以下公式给出:
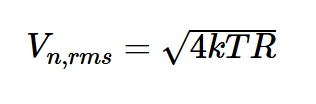
图5显示了计算RS噪声的电路图。
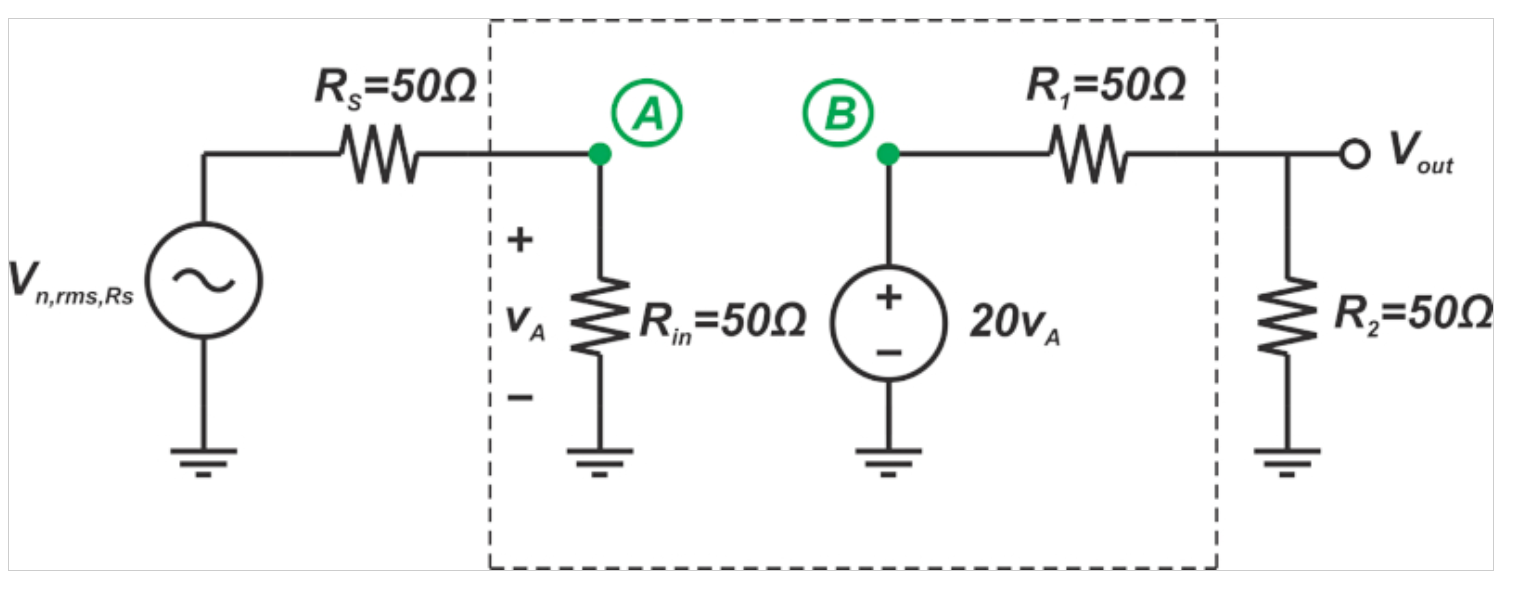
图5。计算RS噪声的示例电路图。
在该图中,输入电压源短路,RS的噪声电压与该电阻器串联。由于RS=Rin,RS的噪声电压在输入端减半,产生的输入噪声功率为:
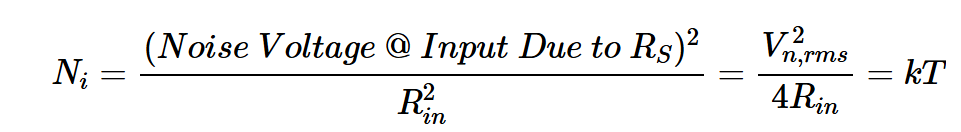
方程式6。
Ni是电路输入端的噪声功率。应当注意,Ni是在假设电路的输入阻抗(Rin)无噪声的情况下计算的。由于Vn,rms在
V/√Hz,
,上述方程给出了每单位带宽的噪声功率(V2/Hz)
因此,方程6的结果应乘以噪声带宽Bn,以找到感兴趣带宽上的总噪声功率。考虑到带宽,方程5和6给出了输入信噪比:
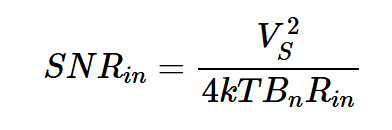
方程式7。
为了计算输出信号和噪声功率,我们需要找到电路的功率增益(输出功率与输入功率的比值):
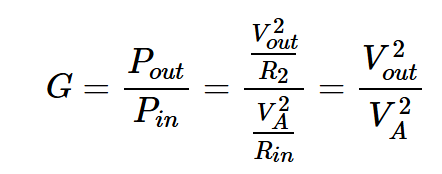
方程式8。
在上述方程中,Vout表示输出电压的RMS。从电路图中,我们注意到:
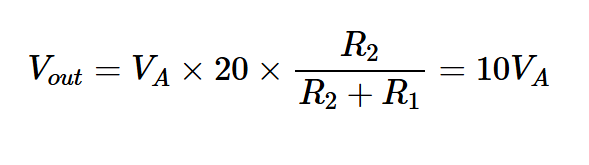
方程式8简化为G=100。输出信号功率计算如下:
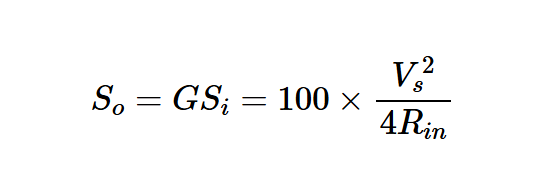
方程式9。
根据方程式6,源电阻引起的输出噪声计算如下:
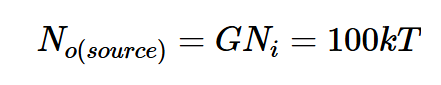
方程式10。
图6显示了计算Rin噪声贡献的电路图。
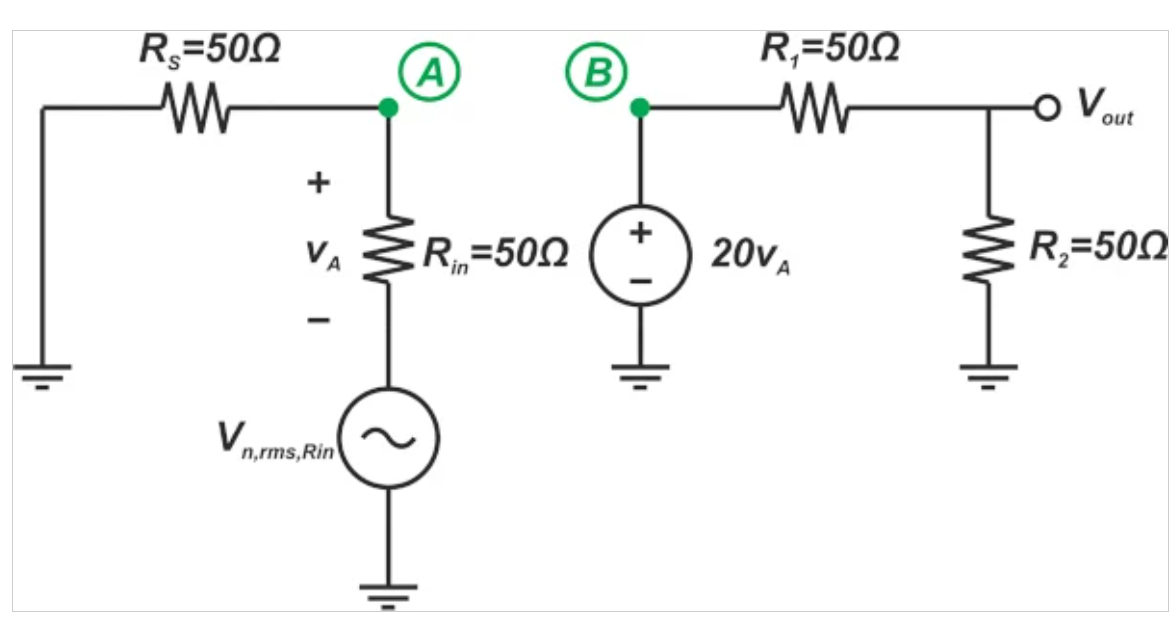
图6。计算Rin噪声贡献的示例电路图。
将上图与图5进行比较,我们可以得出结论,Rin的输出噪声与RS(100kT)的输出噪声相同。每个R1和R2的输出噪声功率可以很容易地计算为kT。因此,总输出噪声为:
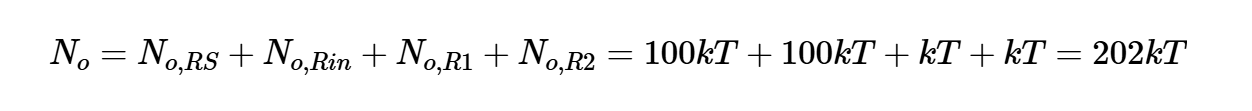
方程式11。
再次注意,方程式10和11给出了每单位带宽的噪声功率(V2/Hz),结果应乘以噪声带宽Bn,以找到感兴趣带宽上的总噪声功率。方程式9和11给出了输出信噪比:
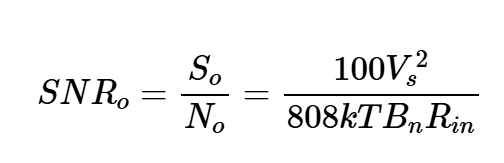
方程式12。
最后,根据方程式7和12,计算噪声系数:
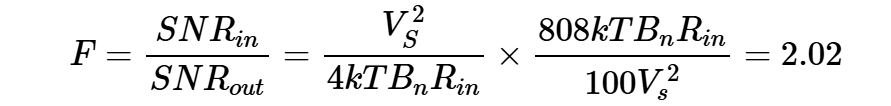
方程式13。
以分贝表示,我们得到NF=3.05dB。现在,让我们使用方程4来分析电路噪声系数。在这种情况下,我们只需要计算源阻抗No(source)产生的输出噪声部分和电路No(added)产生的部分。否(添加)可以根据方程式10和11计算:
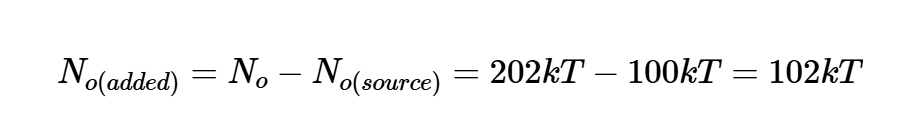
方程式14。
将方程10和14代入方程4,得到:
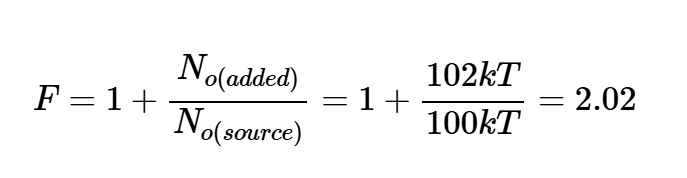
这与之前的计算结果一致。根据方程4,我们不需要计算输入和输出信号功率以及输入和输出信噪比。结果,可以更容易地计算方程4。





评论