什么是抖动？利用抖动消除量化失真的方法

了解如何能够将抖动添加到信号中，以通过消除量化误差和失真来提高模数转换系统的性能。

有时，电子噪音可能是伪装成的福音。在本文中，我们将着眼于“抖动”，这是指在信号中加入适当的噪声成分以提高a/D（模拟到数字）转换系统的性能的技术。

什么是抖动？

大多数电子工程师都熟知限制电子电路中噪声水平的方法。滤波是一种常见的技术，可用于消除噪声分量或至少限制其带宽。在某些应用中，例如去噪头戴式耳机和去噪低噪声放大器（LNA），我们甚至可以测量主要噪声分量，并从系统输出中减去它，以实现所需的性能。

尽管有这些应用，但仍存在模数转换系统，其中我们需要噪声来改善电路性能。这种被称为抖动的信号处理技术有意地将具有适当的PDF（概率密度函数）和PSD（功率谱密度）的噪声信号添加到ADC（模数转换器）输入（采样和量化之前）以改善系统的某些性能方面。图1显示了一个抖动系统的简化框图（该图表示一种被称为非可疑抖动的抖动类型）。

显示抖动系统框图的示例图。

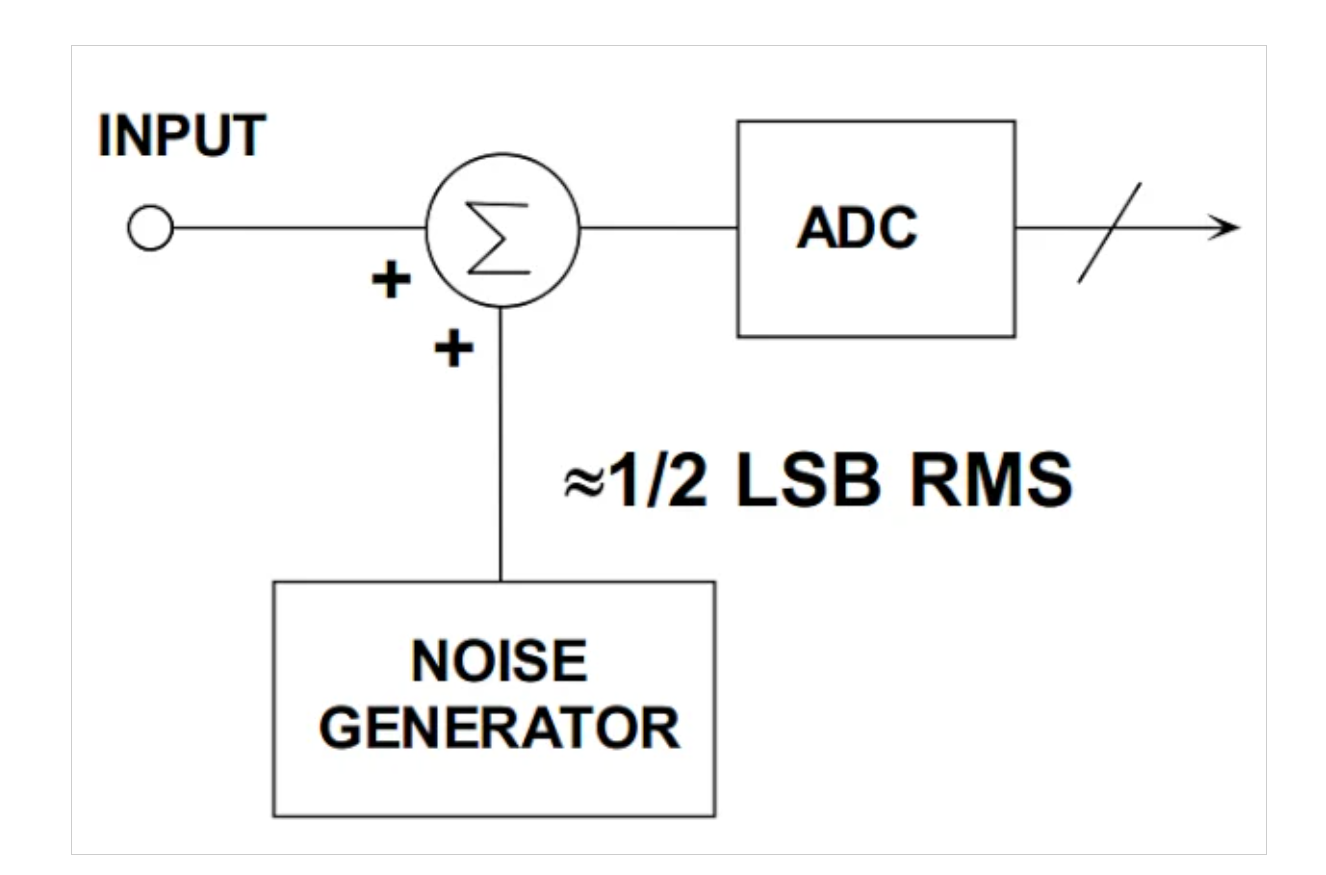
•图1。显示抖动系统框图的示例图。图像由ADI提供

当人们第一次学习到关于抖动的知识时，人们可能会发现某些级别的噪声实际上在某些情况下是有帮助的，这是违反直觉的。抖动技术可用于三个不同的目的：

通过打破量化误差与输入信号之间的统计相关性来改善理想量化器的性能

随机化非理想ADC上的DNL（差分非线性）误差模式，以改善无杂散动态范围（SFDR）性能

通过对慢变信号求平均值来提高测量分辨率

在本文中，我们将讨论抖动如何通过打破量化误差和输入信号之间的统计相关性来改善理想的量化器，但在此之前，我们需要仔细研究ADC量化噪声。

ADC量化高级基础知识

ADC表示通过几个离散电平的模拟值的连续范围，这固有地增加了被称为量化误差的误差。我们进行了大量的研究以充分了解这一错误。研究历史实际上可以追溯到1948年W.R.Bennett发表的论文“量化信号的光谱”。今天，人们广泛知道，在某些条件下，量化误差可以被建模为具有均匀分布的相加噪声

  $\pm \frac{LSB}{2}$ 

LSB（LSB表示转换器的最低有效位）。

此外，假设量化噪声是白噪声（即，在奈奎斯特带宽dc到fs/2均匀扩散），总功率等于

 $\frac{LS{B}^2}{12}$

平谱特性是基于量化误差样本彼此不相关的假设。

在本文中，我们将把这个量化误差的模型称为“量化噪声模型”。我们将很快讨论量化噪声模型并不总是有效的；然而，对于许多实际应用来说，它还足够精确。下面的例子说明了为什么处理数据转换器的EE喜欢这个模型！

10位vs 12位ADC：多少位就足够了？

让我们考虑其中ADC的参考电压为2V的应用。假设ADC输入信号具有1mV RMS（均方根）的噪声。使用10位ADC时，LSB

$\frac{2}{2^{10}}$ = 1.95 mV

，因此，噪声的RMS值等于0.51 LSB。

 $\frac{LSB}{\sqrt{12}}$ = 0.29 LSB

从量化噪声模型可知，量化运算增加了RMS噪声

如您所见，量化噪声与来自输入的原始噪声相当。要求出系统的总噪声功率，我们应将两个噪声源的功率加在一起：

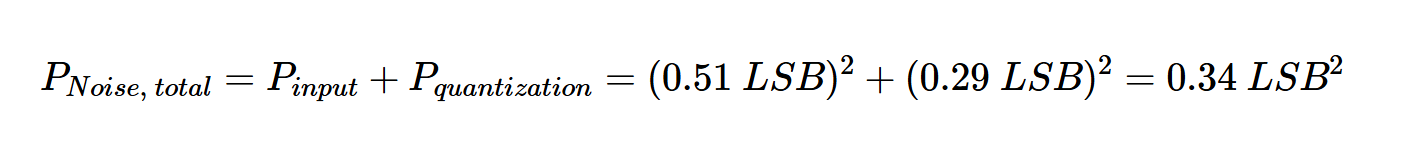
取该值的平方根得出总噪声的均方根值为0.59 LSB。如果这个噪声水平对于我们的应用是不可接受的，那么我们可以增加ADC分辨率以减少量化噪声。例如，对于12位ADC，输入噪声是2.05 LSB RMS。与输入噪声相比，量化噪声（0.29 LSB）现在几乎可以忽略不计。本例的总噪声均方根值为2.07 LSB。12位系统似乎为这种应用提供了足够的分辨率。

在我们的信号中存在总噪声的情况下，我们可以确定交流应用中的信噪比（SNR）或测量应用中的最小可检测信号。这里重要的一点是，噪声模型允许我们容易地考虑量化过程对系统的噪声性能的影响。

作为补充说明，值得一提的是，上述讨论隐式地假设由ADC添加的主导噪声是量化噪声。。随着ADC分辨率的增加，量化噪声变得越来越小。在某些点上，与ADC内的由ADC内部电路的热噪声和闪烁噪声产生的电子噪声相比，量化噪声变得可忽略不计。今天的高分辨率Δ∑（Δ∑）ADC就是这种情况。如果量化噪声可忽略不计，则应考虑ADC的峰-峰值输入相关噪声来分析系统噪声性能。

量化的频率含量

量化噪声模型的一个暗示是误差与输入不相关。为了更好地理解这一点，请考虑图2中的波形。

•波形示例。

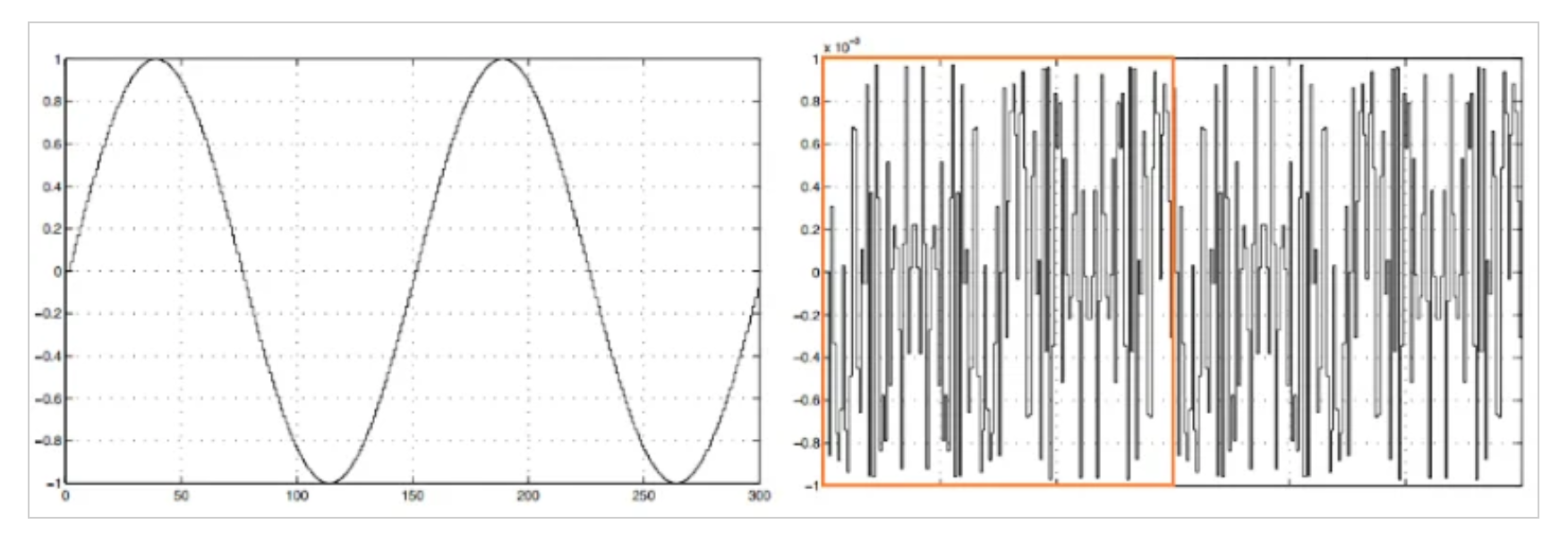
•图2。•波形示例。图片由Franco Maloberti提供

上图中的左曲线描绘了10位量化正弦波的两个周期。）。在这个例子中，采样频率与输入频率的比值是150。您可以通过目视检查确认量化误差是周期性的（一个周期由橙色矩形表示）。另外，在输入和量化误差信号之间存在相关性。由此可知，周期性信号的频率内容集中于信号的基波频率的倍数。这意味着虽然量化噪声模型希望误差具有平坦的频谱，但是量化误差具有一些强的频率分量。

这是一个普遍的问题：如果输入是正弦波并且采样频率是输入频率的倍数，那么量化误差与输入信号相关。。

显示相关噪声（a）和不相关噪声（b）的示例图。

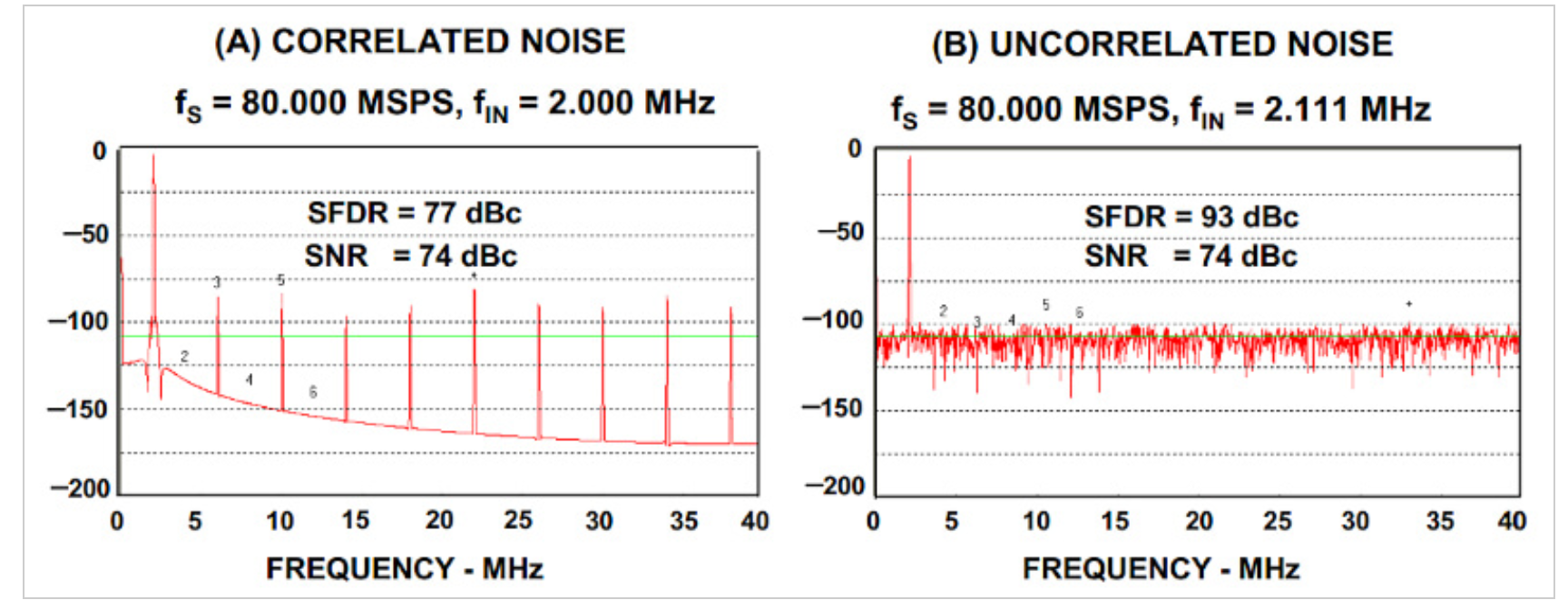
•图3。显示相关噪声（a）和不相关噪声（b）的示例图。图像由ADI提供

左边的曲线显示了当输入为2MHz正弦波并且采样频率为80MSPS时理想的12位ADC的频谱。右曲线显示了在相同采样频率下采样的2.111 MHz正弦波的相同ADC的频谱。正如预期的那样，当采样频率与输入频率的比值为一个整数时，在输出端产生输入频率的不同谐波。对于左侧曲线，系统的无杂散动态范围（SFDR）仅为77 dBc。通过略微改变输入频率，谐波分量消失，我们得到了一个草籽状的噪声基底。

注意，量化误差的RMS值对于两种情况都相同，导致74dBc的SNR（通过12位ADC可获得的理论值）。对于这两种情况，RMS误差与量化噪声模型预测的值一致

(LSB√12)

；然而，在左图中误差的频谱并不平坦。

上述谐波分量是量化过程的伪像，并且与ADC电路的性能无关。这突显了ADC测试的一个重要注意事项：如果输入信号是采样频率的精确倍数，那么我们针对单音正弦波快速傅里叶变换（FFT）测试获得的频谱将受到量化过程伪像的影响。

总之，如果量化误差与输入相关，我们不能假设ADC仅增加输入的噪声本底。在这种情况下，量化噪声模型不再有效，并且量化过程可以在输出频谱中产生显著的谐波分量。通常情况下，我们更喜欢误差能量在宽频带上传播，而不是集中在某些特定的频率上。

量化低振幅信号

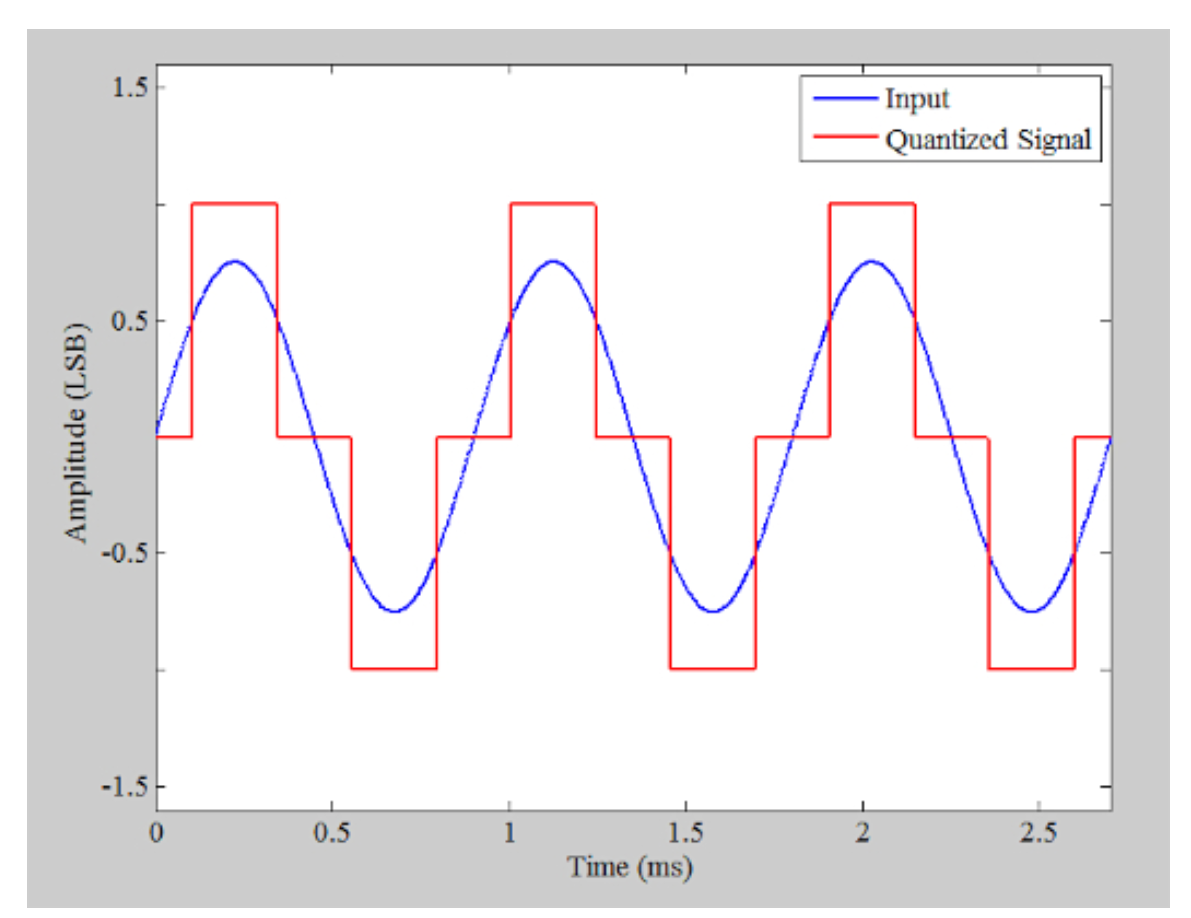
量化低振幅信号还可以导致量化误差和输入之间的相关。其中低振幅信号可能成为问题的示例应用是数字音频系统。假设ADC输入的振幅降到0.75 LSB，如图4所示。

显示ADC输入下降幅度的示例图。

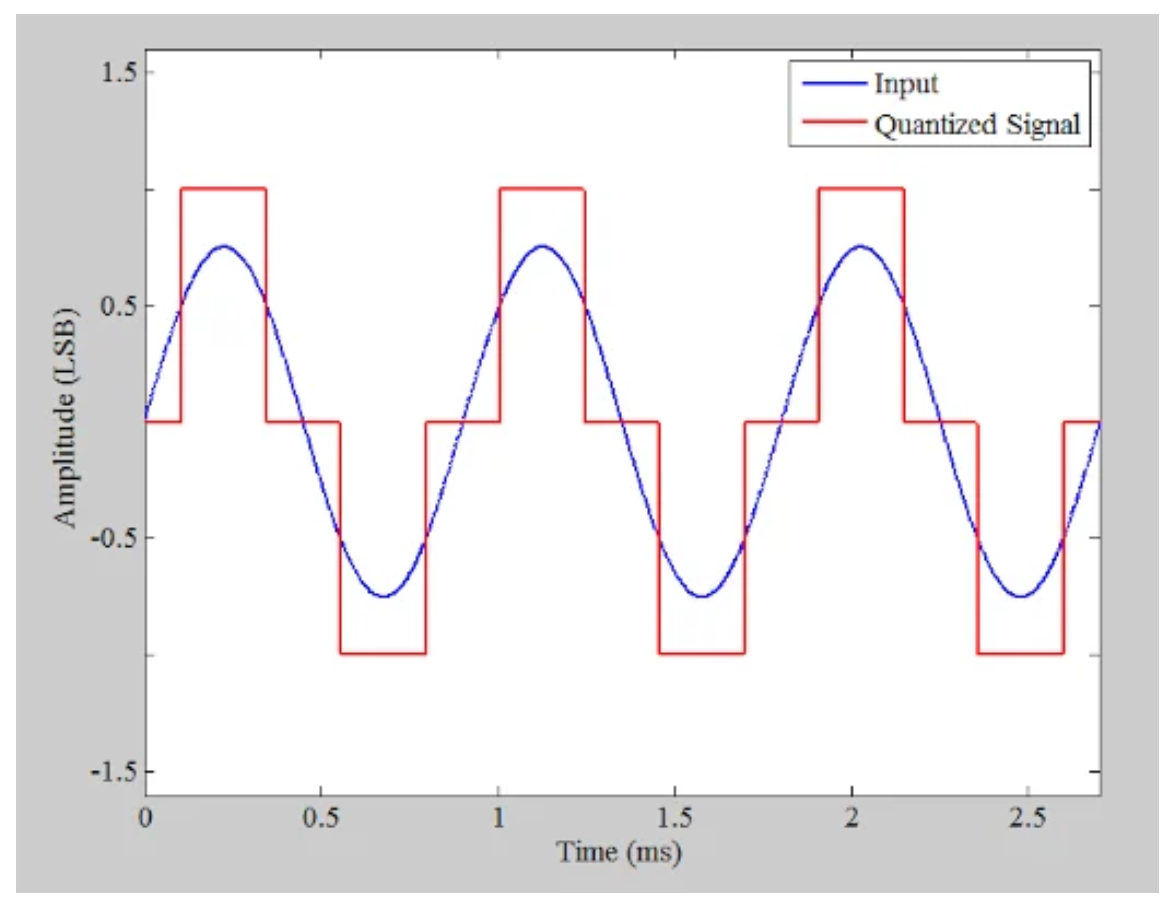
•图4。显示ADC输入下降幅度的示例图。

 如您所见，量化信号仅取三个不同的值，并且具有方波状的形状。我们知道方波的频谱包含基波频率的不同谐波。在上面的例子中，输入是1.11kHz的正弦曲线，并且采样频率是400kHz（故意选择为远高于奈奎斯特采样定理所要求的采样频率）。输出的FFT如图5所示。

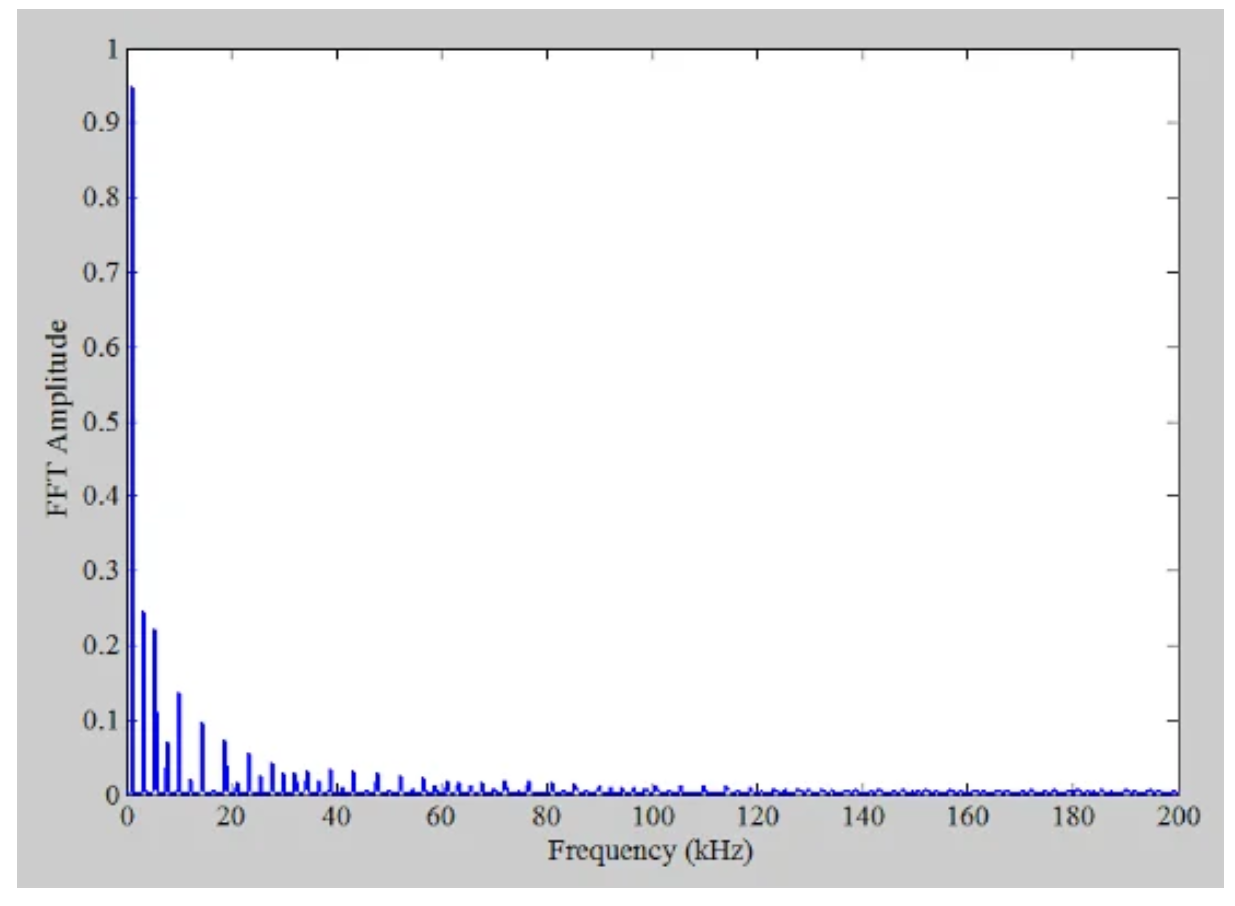
•图5。

虽然输入频率（1.11 kHz）不是采样频率（400 kHz）的倍数，但频谱包含显著的谐波分量。这些谐波在图6中提供的放大版本的光谱中更容易识别。

放大版本的频谱。

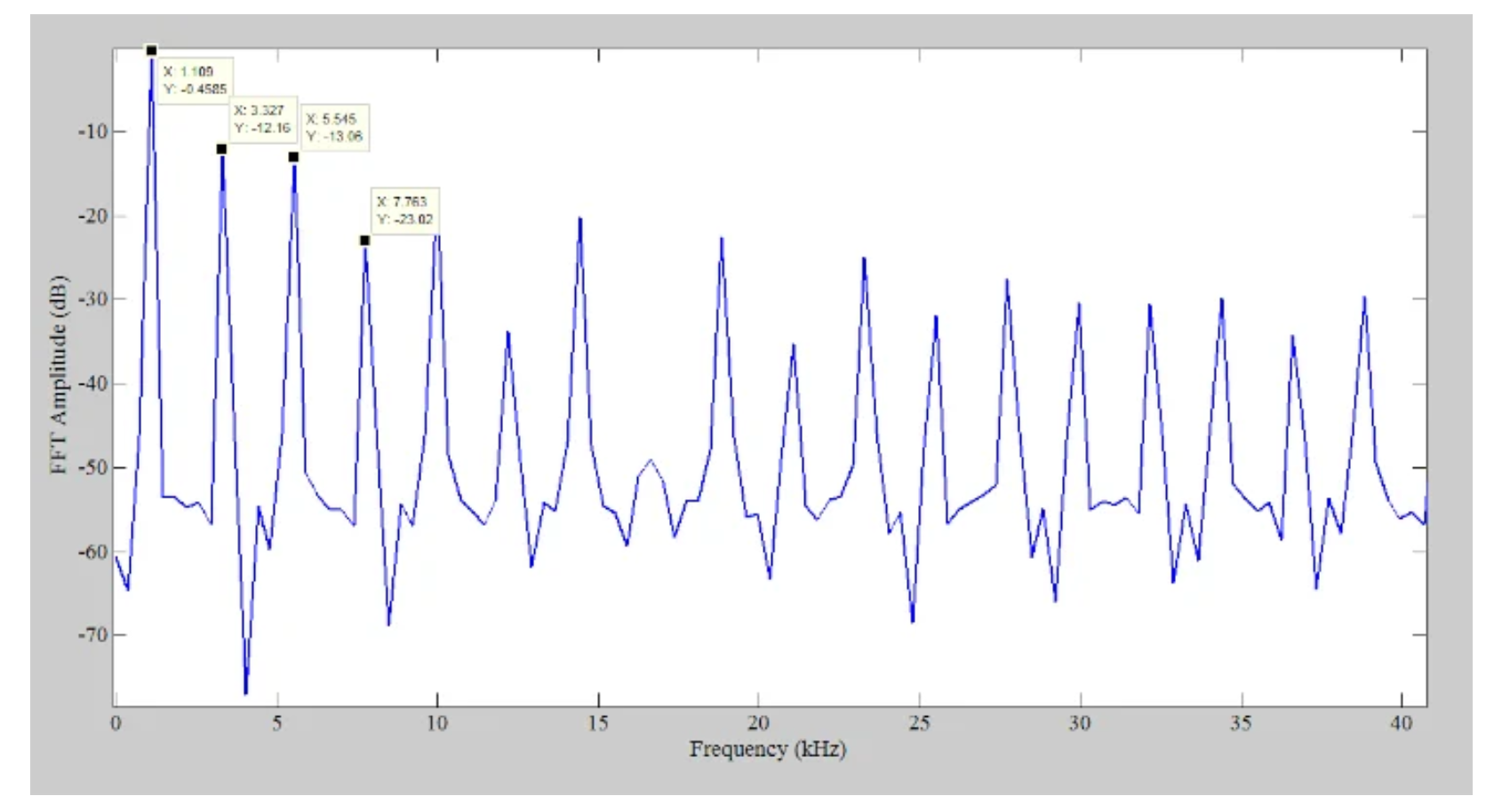
•图6。放大版本的频谱。

抖动的优势

为了检验抖动技术，我们在上述信号中加入具有三角形分布的噪声，然后对其进行量化，三角形抖动pdf（概率密度函数）的宽度取为2 LSB。。

加入具有三角形分布的噪声并进行量化后的示例波形。

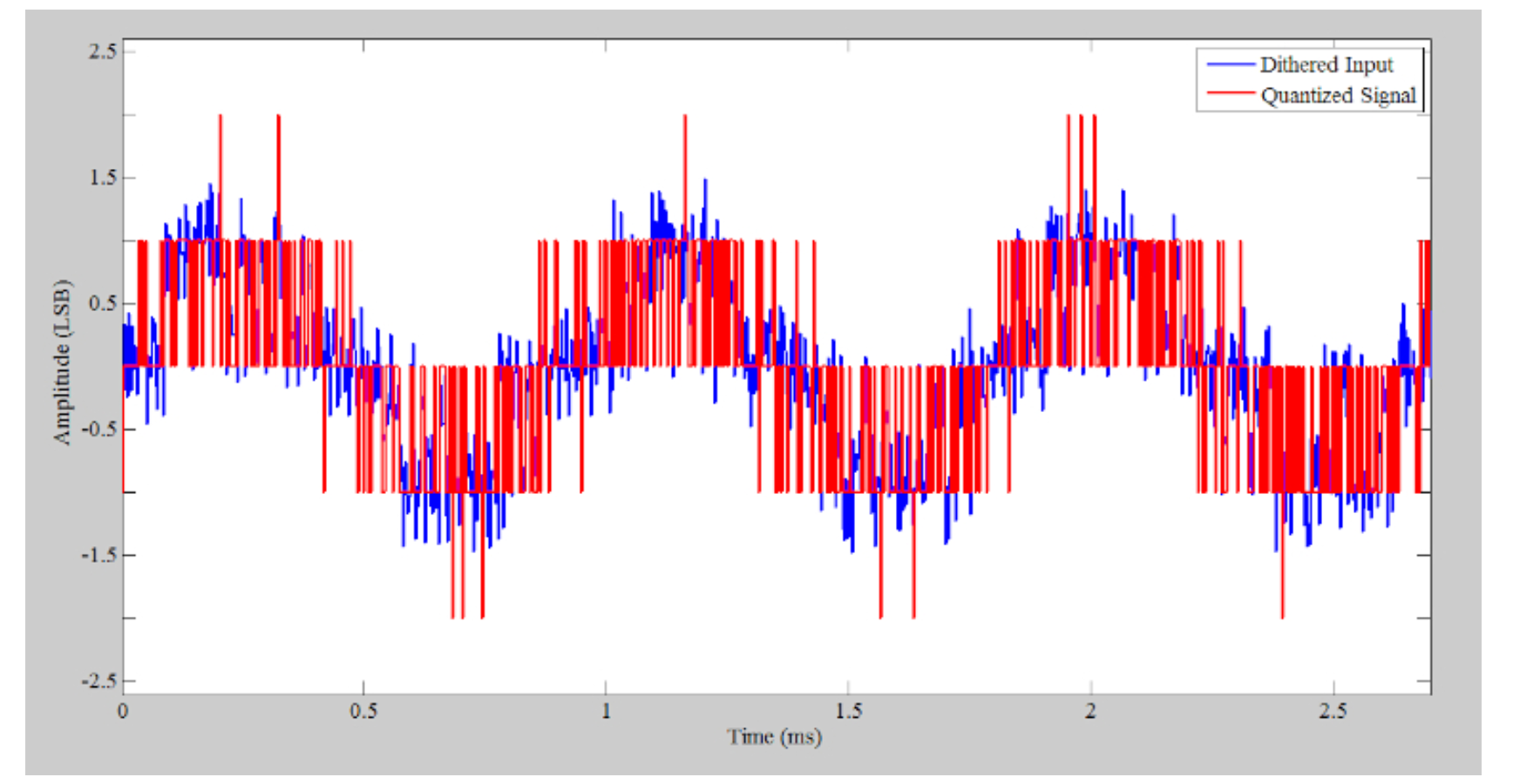
•图7。加入具有三角形分布的噪声并进行量化后的示例波形。

在时域中，信息似乎丢失了，但频域又如何呢？新量化信号的频谱（上面的红色曲线）如图8所示。

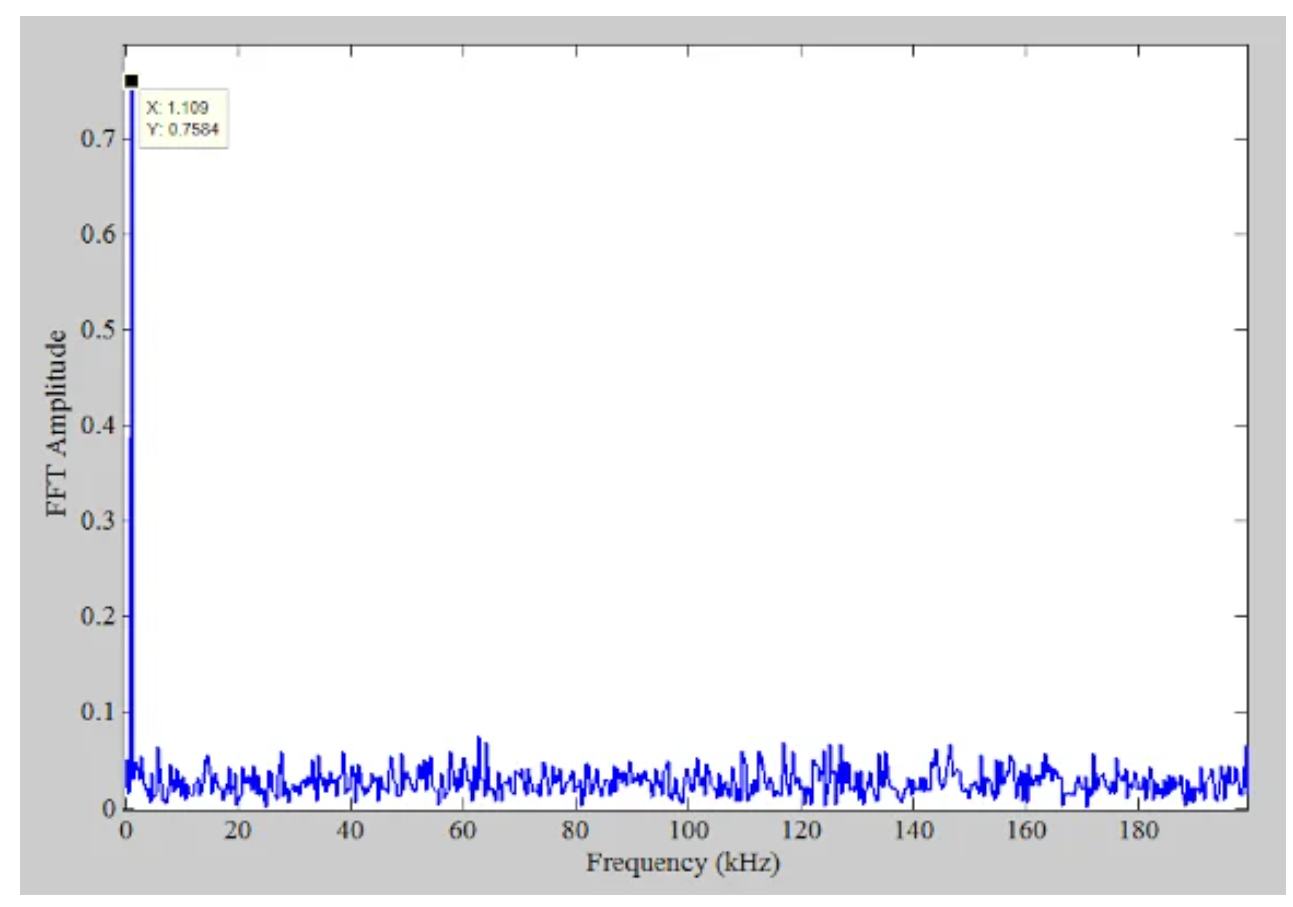
•图8。

消除谐波。实际上，谐波分量的能量在宽频带上传播。因此，当我们应用抖动技术时，我们期待噪声本底略微上升。除了这种效果之外，添加到输入中的抖动噪声也有助于噪声本底的增加。

上面的例子清楚地显示了在光谱分析应用中的抖动的优点。然而，有趣的是注意到，即使不将信号转换到频域，我们也可以受益于抖动。例如，在数字音频中，无特征背景噪声的增加（由于抖动）在感觉上远比量化器引入的人工谐波更可接受。

受益于抖动噪声

量化噪声模型的一个暗示是量化误差与输入不相关。当不是这种情况时，量化操作引入了一种有时被称为“量化失真”的类型的失真。通过添加抖动噪声，消除了量化误差和输入之间的关联。因此，这消除了由量化操作产生的谐波分量。通过这种方式，抖动可以改善理想量化器的性能。如上所述，抖动也用于其他几个目的。在本系列的下一篇文章中，我们将更深入地探讨这个讨论。

最后值得一提的是，在大多数系统中，输入信号具有足够的噪声，因此不需要添加额外的抖动噪声来破坏量化噪声和输入之间的相关性。而且，ADC的输入相关噪声可能足以产生相同的抖动效果。