理解D类放大器的非理想性:无功负载和寄生电容
在本文中,我们将了解D类功率放大器的两个重要非理想性以及它们如何影响性能。
本文引用地址:https://www.eepw.com.cn/article/202409/462692.htm正如我们从之前的文章中所知,实际D类放大器的开关频率并不总是与其谐振频率相匹配。这种失配可能是由于组件非理想性或放大器在略微不同的频率下有意操作造成的。在这两种情况下,失谐LC电路都会产生无功负载。
在本文中,我们将研究当D类放大器的负载网络具有电抗性组件时,其性能是如何受到影响的。我们还将探讨调谐电路输入端寄生电容的影响。对每个非理想性的讨论将以一个示例问题结束。
无功负载引起的功率损失
图1显示了我们在过去几篇文章中一直在探索的互补电压开关D类放大器。
互补电压开关D类配置。
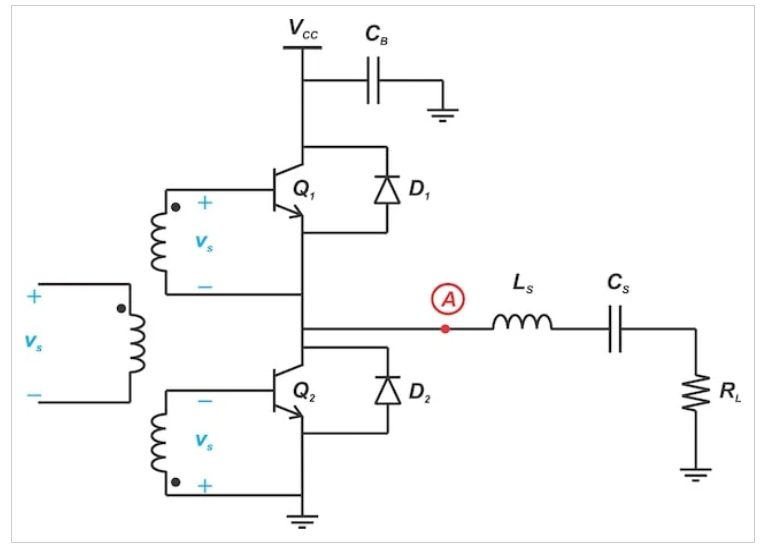
图1。互补电压开关D类配置。
对于上述放大器,理想电感值为Ls。理想电容为Cs。Ls和Cs共同为我们提供了一个调谐到开关频率的理想谐振电路。
然而,假设由于元件的非理想性,电感实际上是(Ls+La)。如图2所示,我们现在有一个与理想调谐电路串联的额外电感。
一种D类放大器,由于元件非理想性,LC电路失调。
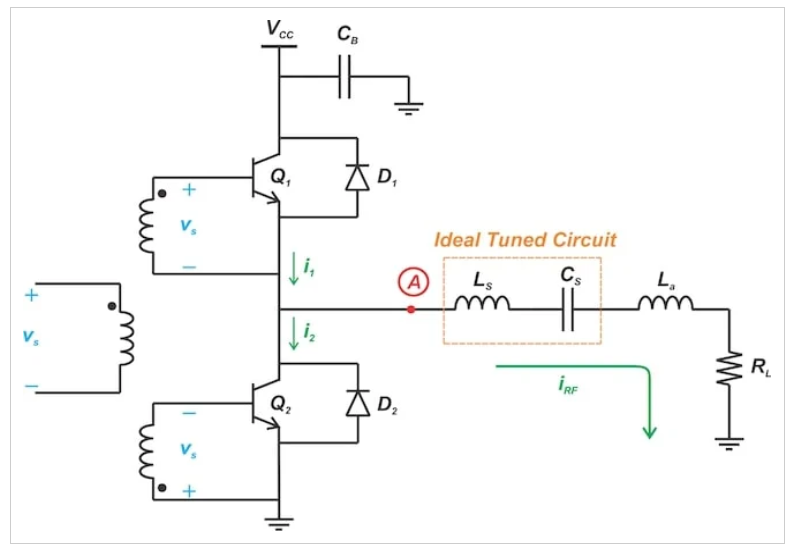
图2:一种D类放大器,由于元件非理想性,LC电路失调。
橙色盒子中的理想调谐电路在开关频率下充当短路。剩余的负载网络包括La和RL的串联连接。由于负载是电感性的,我们在图3中看到,输出电流(iRF)滞后于节点A(VA)处方波的基波分量。
在谐振频率以上,电流滞后于方波电压的基波分量。
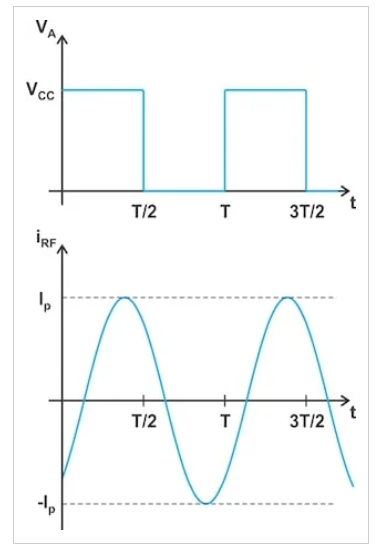
图3。在谐振频率以上,电流滞后于方波电压的基波分量。
从我们对D类操作的第一次讨论中,我们知道理想的D类放大器具有理论上100%的效率和PL=2VCC2/π2RL的输出功率。让我们看看图3中的相位差是如何影响这些参数的。
无功负载对输出功率的影响
我们需要知道负载电流的峰值(Ip)来计算输送到负载的功率。负载电流由VA的基波分量产生。使用傅里叶级数表示法将VA表示为其组成频率分量,我们得到:
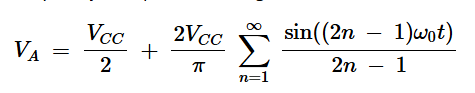
方程式1。
其中⍵0是方波的角基频。
从方程1中,我们看到VA的基本分量具有2VCC/π的峰值。与我们讨论理想D类放大器时相比,该方程及其结果都没有变化。
方程式2则不然。开关频率(⍵0)下的负载阻抗(ZL)不再简单地等于RL。相反,它由La和RL的串联连接组成,给我们一个阻抗:
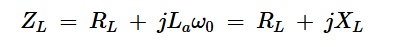
方程式2。
其中XL是电感电抗。根据欧姆定律,流经负载的电流为:
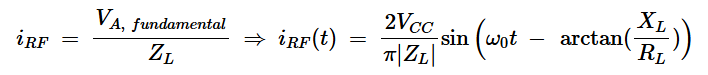
方程式3。
根据方程式3,iRF的峰值为
Ip = 2VCCπ|ZL|.
又因为irms等于 Ip/√2,
,我们现在可以计算输送到负载的平均功率:
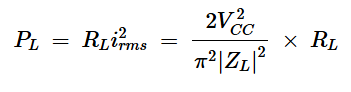
方程式4。
这个方程式可以改写为:
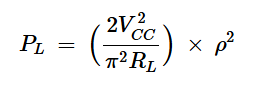
方程式5。
解释:
2V2CCπ2RL 是输送到纯电阻性(XL=0)负载的功率
⍴=RL/|ZL|
由于负载阻抗包括电抗分量,⍴小于1。因此,方程式5的乘积小于理想负载功率。
添加无功分量会降低负载功率,这并不奇怪——从方程2中很容易看出,无功项会增加负载阻抗(|ZL|)的大小,从而降低输出电流。
无功负载对效率的影响
在上一节中,我们计算了输出功率。为了找到效率,我们还需要确定电源提供的输入功率。输入功率等于电源电压乘以从电源汲取的电流的平均值。
在图3的波形中,在开关周期的前半个周期(从t=0到t=t/2),即上开关打开时,电流从电源中汲取。在后半个周期,上开关打开,无法从电源中吸取电流。在这半个周期中,存储在LC电路中的能量通过负载和下部开关循环。因此,电源电流的直流分量为:
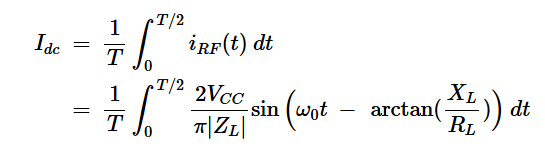
方程式6。
请注意,积分是在上部开关打开的时间间隔内进行的。
上面看似令人生畏的方程式简化为:
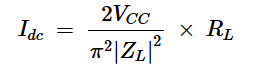
方程式7。
将方程7乘以VCC,我们得到输入功率:
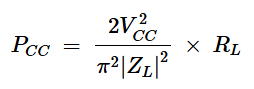
方程式8。
这等于输出功率(方程式4),从而得到100%的理想效率。即使无功负载降低了输出功率,也不会降低放大器的效率。
示例:无功负载引起的功率降低
在讨论理想的D类放大器时,我们设计了一个互补电压开关D类放大器,为纯电阻50Ω负载提供20 W的功率。我们看到,这需要VCC=70.2 V的电源电压和可以安全传导0.89 a最大电流的晶体管。您可以通过将RL=50Ω和XL=0代入本文的方程式3和5来验证这些数字,因为纯电阻负载是我们上面提供的分析的一个特例。
这一次,让我们假设RL=50Ω串联出现50Ω的电抗。输出功率和最大集电极电流是多少?
首先,让我们找到⍴。当RL=50Ω和XL=50Ω时,我们得到:
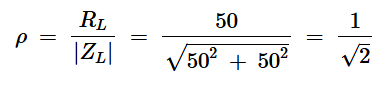
方程式9。
将⍴的值代入方程5,我们观察到由于负载网络的无功分量,输出功率减半。电阻负载的输出功率为20 W,因此新的输出功率是0.5×20=10 W。
在方程式3中,我们看到最大电流为
Ip = 2VCCπ|ZL|.
|ZL|等于RL/⍴,VCC在示例开始时为70.2 V。因此,我们有一个峰值电流:
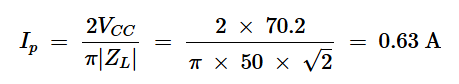
方程式10。
通过晶体管的最大电流从0.89A(在理想放大器中)减小到0.63A。如上所述,输出功率从20W减半到10W。
寄生电容引起的功率损失
图4显示了D类放大器的另一个重要的非理想性:寄生电容。
Cc1和Cc2对与Q1和Q2并联的寄生电容进行建模。
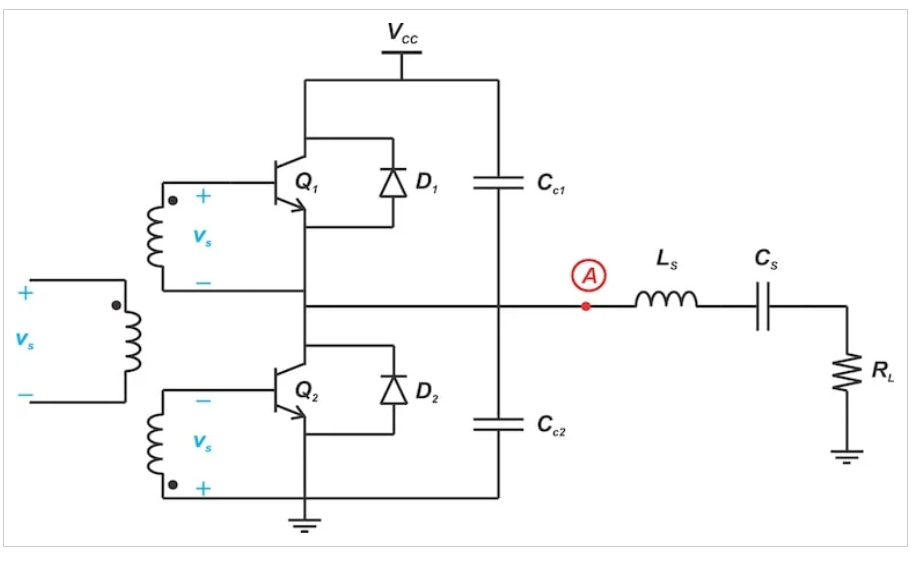
图4。Cc1和Cc2对节点A和电源轨之间存在的寄生电容进行建模。
在上图中,Cc1和Cc2是与Q1和Q2并联出现的等效寄生电容。当方波在电源轨之间转换时,电容会导致节点A的功率损失。让我们看看这对放大器的性能有何影响。
图5(a)提供了操作前半周期电路的简化模型。图5(b)对下半周期也进行了同样的操作。每个半周期的Cc1和Cc2处的电压以绿色表示。
在一个操作周期内具有寄生电容的D类放大器的简化模型。
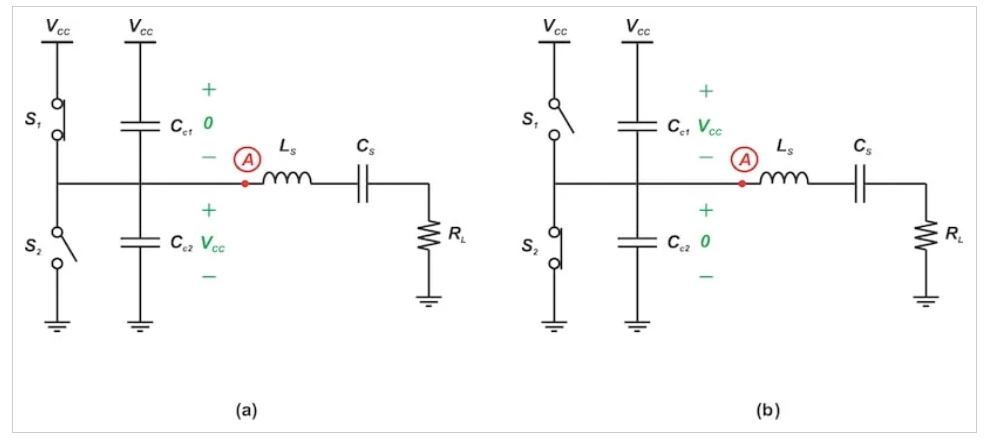
图5。当节点A被驱动到VCC(A)和地(b)时,Cc1和Cc2处的电压。
在循环的前半部分,上开关(S1)闭合,下开关(S2)打开。因此,节点A处的方波被驱动到VCC。由于其两个端子处于相同的电势,Cc1没有电荷。同时,Cc2被充电到VCC。
在第二半周期开始时,S2关闭,S1打开。节点A处的电压被驱动——理想情况下是立即——接地。当发生这种转变时,S2将Cc1充电到VCC,并将Cc2从VCC放电到0V。因此,最初存储在Cc2中的能量损失了。
使用电容器中的能量存储公式,我们可以计算出Cc2的初始能量:
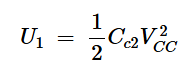
方程式11。
当它关闭时,这种能量在S2中以热量的形式消散。同时,Cc1被充电到VCC。将存储在Cc1中的能量表示为U2,我们有:
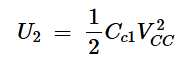
方程式12。
为了了解这如何影响功率损耗,我们需要查看图6中简单RC电路的行为。
给电容器充电的RC电路。
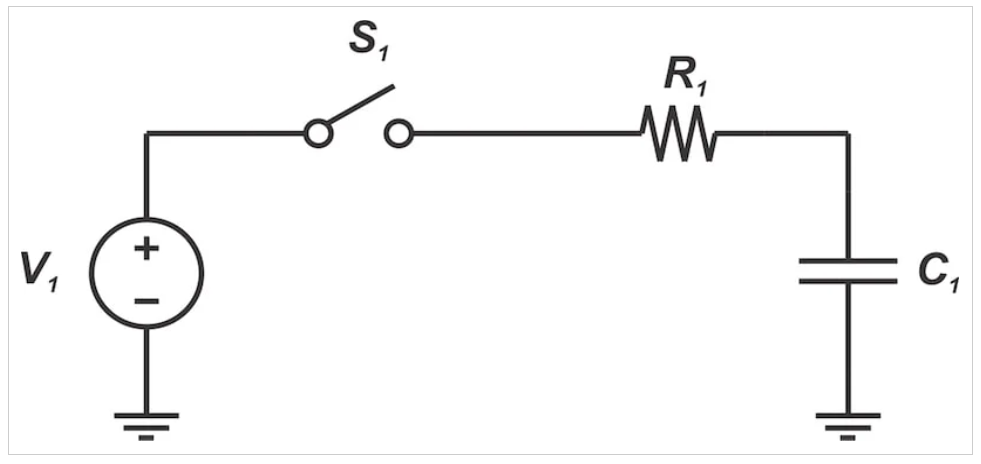
图6。给电容器充电的RC电路。
当我们闭合这个电路中的开关时,电压源提供能量给电容器充电。然而,可以证明,电池提供的能量中只有一半存储在电容器中。另一半在电阻器中以热量的形式消散。
有趣的是,电阻器中耗散的能量与电阻值无关。在D类放大器中,这意味着当S2闭合并对Cc1充电时,等于U2的能量在导通电阻中耗散。因此,S2中耗散的总能量为U1+U2。
在下一个半周期开始时,当节点A被驱回VCC时,会发生类似的事件序列。此时,开关S1闭合以将Cc1放电至0V并将Cc2充电至VCC。这导致了U1+U2的另一个能量损失。因此,在整个周期内,由于寄生电容而损失的总能量为:
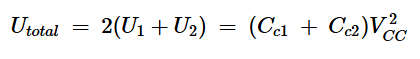
方程式13。
由于在每个射频周期中都会损失一定量的能量,因此消耗的功率为:
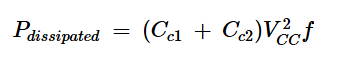
方程式14。
其中f是开关频率。
因为这种功率在开关中耗散,所以对放大器的输出功率没有影响,只对其效率有影响。
示例:寄生电容导致的效率降低
由VCC=70.2 V供电的互补电压开关D类放大器为50Ω负载提供20 W的功率。然而,在其调谐电路的输入端存在两个20pF的寄生电容(Cc1=Cc2=20pF)。如果开关频率为10MHz,由于寄生电容器损失了多少功率?放大器的效率是多少?
将这些数字代入方程14,我们得到:
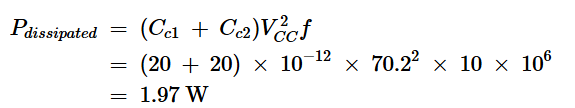
方程式15。
电容导致1.97W的功率损失。
如上所述,寄生电容引起的功率损耗不会影响输出功率。它们只会增加电源提供的功率。因此,效率可以计算为:
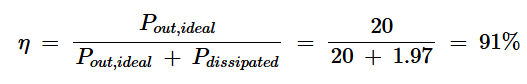
方程式16。
由于寄生电容,D类放大器的效率为91%,而理想的D类放大器理论效率为100%。
总结
在本文中,我们了解了影响D类放大器的两个非理想因素——无功负载组件和寄生电容。我们发现,无功负载会降低放大器的输出功率,但不会降低其效率;另一方面,寄生电容会降低效率,但不会降低输出功率。
与前面关于D类放大器的文章一样,我们的讨论是基于互补电压开关配置的。在下一篇文章中,我们将介绍一种不同的配置:变压器耦合电压开关D类放大器。





评论