新闻中心

EEPW首页 > 测试测量 > 设计应用 > 侧向仪器中数字相敏检波算法的改进与实现

侧向仪器中数字相敏检波算法的改进与实现

作者：张森峰,高秀,晓陈文,戴光明,姚德忠,张年英 时间：2020-11-18 来源：电子产品世界
收藏
编者按：本文提出了一种基于数字低通滤波的对现有传统数字相敏检波算法的改进方法，并对其进行了仿真与实现。介绍了传统数字相敏检波的基本原理，给出了相关的计算方法。阐述其精度不足的缺点，然后给出基于数字低通滤波的改进方案。使用MATLAB对改进前后两种方案进行仿真与比较，以明确它们在精度上的差异，展现改进算法的优越性。最终使用C语言对算法进行实现，以方便其移植到DSP上进行实际的工程应用。基于低通滤波的数字相敏检波算法虽然会较大程度上增加计算量，但是却可以得到更高的精度。

作者简介，张森峰（1980-），男，山西，硕士，中国石油测井技术研究院，工程师，从事测井仪器研发工作。

本文引用地址：https://www.eepw.com.cn/article/202011/420414.htm

0  引言

在侧向测井中，侧向仪器通过发射电极向地层发射不同频率的正弦信号，通过其变化情况来反映地层电阻率。但是接收到的信号是多种频率的混合信号，而且还会夹杂着各种噪声。因此，如何精准地从其中提取出某一特定频率的正弦信号，进而计算它的幅值与相位变化，就成为了真实客观地反映地层电阻率情况的决定性因素。

相敏检波技术被用来解决上述问题，但是不同的实现方案使得最终的实际效果与精度亦有不同。早期采用模拟电路来实现相敏检波，但因为三极管的压降导致精度不高[1]。随着数字信号处理理论与技术的发展，基于DSP的数字相敏检波得到了广泛应用，使精度得到了极大的提升。这里对当前数字相敏检波进行改进，以得到更高的精度。

0.png

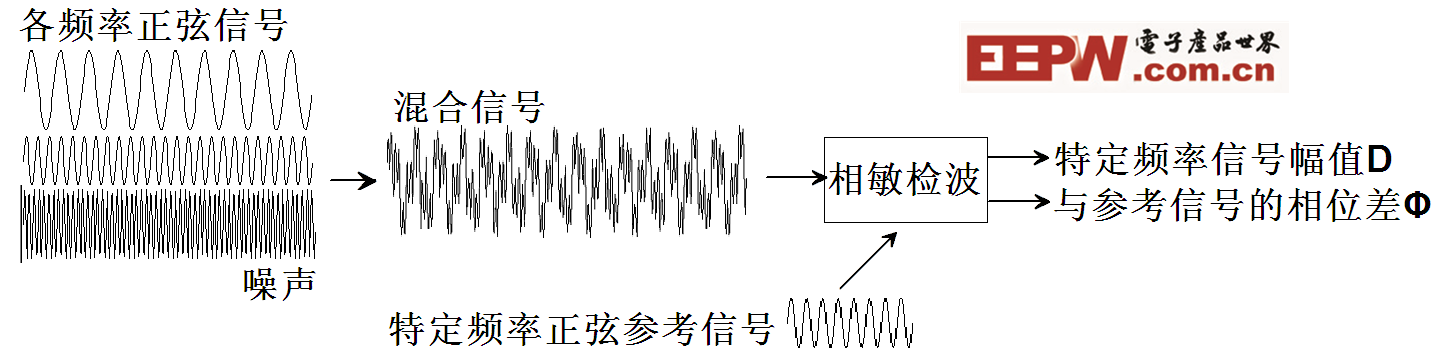
图1 数字相敏检波的功能示意图

1  数字相敏检波原理

数字相敏检波的功能示意如图1。

假设测量信号d(t)为

image.png

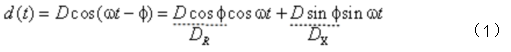
此式中，D为被测信号幅度；ω为被测信号和参考信号的频率；φ为被测信号与参考信号之间的相位差。

我们将Dcosφ记为DR，Dsinφ记为DX。它们分别为被测信号幅值的实部与虚部。

再设

image.png

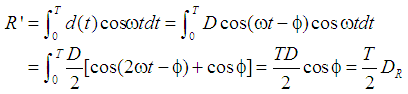
所以有

image.png

同理

image.png

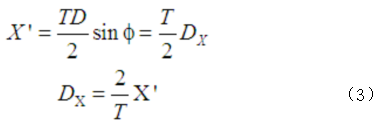
被测信号幅值与相位为[3]

image.png

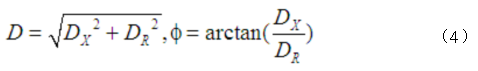
这些数学的推导为我们揭示了实现数字相敏算法的具体计算方法[2]，如图2。

1.png

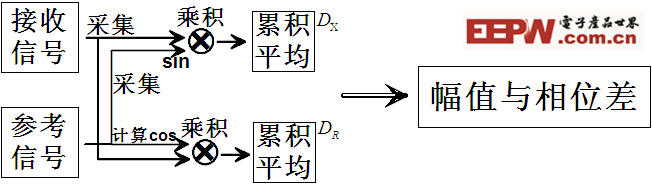
图2 数字相敏检波算法的实现过程

2  数字相敏检波改进

上述实现方法，其实质是积分后再取平均，可以认为是一个均值滤波的过程。既然如此，我们可以向其中引入更有效的滤波算法，以使最终的计算结果精度更高。通过对上面的数学推倒进行改进，可以得到。

image.png

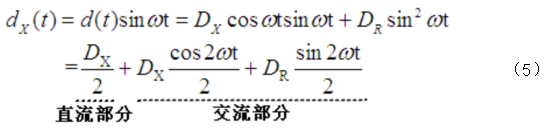
同理

image.png

上式中，通过推导分离出直流与交流两个部分，可以使用低通滤波将其交流部分去掉，最终可得到直流部分，即被测信号幅值的实部与虚部。

具体实现过程如图3。

2.png

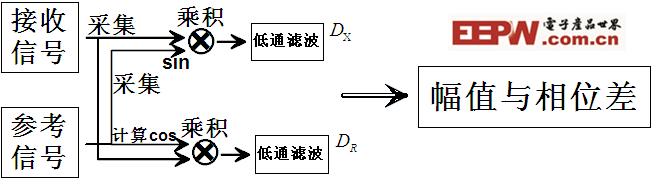
图3 使用低通滤波对数字相敏检波的改进

3  数字相敏检波的MATLAB仿真与对比

使用MATLAB软件对数字相敏检波算法改进前后进行仿真与对比，进而对其具体表现进行评价。

MATLAB仿真如图4所示。


图4 使用MATLAB对改进前后数字相敏检波进行仿真与对比

图4中的低通滤波器由MATLAB的滤波器设计工具FDATool生成[4]。采用四阶巴特沃兹低通滤波器，截止频率为5Hz。

对它们计算精度的对比如表1。

表1 改进前后数字相敏检波计算结果对比表

参考信号频率

（Hz）

相位差

(设置值)

相位差计算值

（改进前）

相位差计算值

（改进后）

幅值

（改进前）

幅值

（改进后）

35

0.1000

0.1007

0.1001

1.2510

1.2500

35

0.2300

0.2306

0.2301

1.2510

1.2500

35

0.3500

0.3504

0.3501

1.2510

1.2500

35

0.6700

0.6701

0.6700

1.2510

1.2500

35

1.2300

1.2300

1.2300

1.2500

1.2500

35

2.8900

2.8900

2.8900

1.2510

1.2500

162

0.1000

0.1007

0.1000

0.7504

0.7500

162

0.2300

0.2307

0.2300

0.7506

0.7500

162

0.3500

0.3506

0.3500

0.7507

0.7500

162

0.6700

0.6701

0.6700

0.7509

0.7500

162

1.2300

1.2290

1.2300

0.7508

0.7501

162

2.8900

2.8900

2.8900

0.7489

0.7501

288

0.1000

0.09827

0.1001

0.5000

0.5001

288

0.2300

0.2289

0.2300

0.4998

0.5001

288

0.3500

0.3495

0.3500

0.4998

0.5001

288

0.6700

0.6711

0.6698

0.5001

0.5001

288

1.2300

1.231

1.230

0.5017

0.5000

288

2.8900

2.884

2.890

0.4970

0.5001

注：35Hz、162Hz与288Hz为三路正弦信号，其幅值分别为2.5V、1.5V与1.0V。

表1很明显地体现了加入低通滤波之后的数字相敏检波在计算精度上普遍高于改进前。这表明了它具有显著的精度优势与实用价值。

4.png

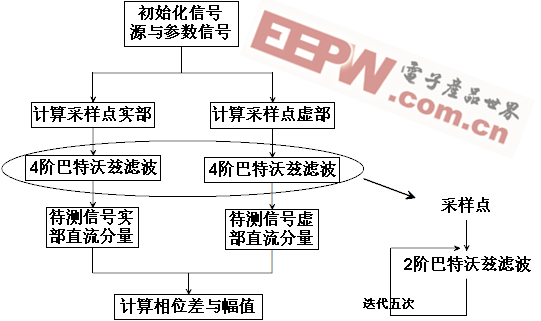
图5 改进后数字相敏检波的实现过程

4  改进后数字相敏检波的实现

改进后的数字相敏检波加入了数字低通滤波器。为了便于此算法在实际侧向仪器中得以应用，需要使用C语言来对其进行实现。因为C语言本身较好的可移植性，故此选取VC++6.0作为开发工具。数字低通滤波器的代码实现得益于MATLAB的FDATool所生成的参数。最终整体实现过程如下。

上图中2阶巴特沃兹滤波根据Direct Form I型 IIR滤波差分方程[5]进行实现。

a0*y[n]=b0*x[n]+b1*x[n-1]+b2*x[n-2]-a1*y[n-1]-a2*y[n-2]

经过5次迭代实现四阶低通滤波。

在VC++6.0中的运行效果如图6所示。

5.png

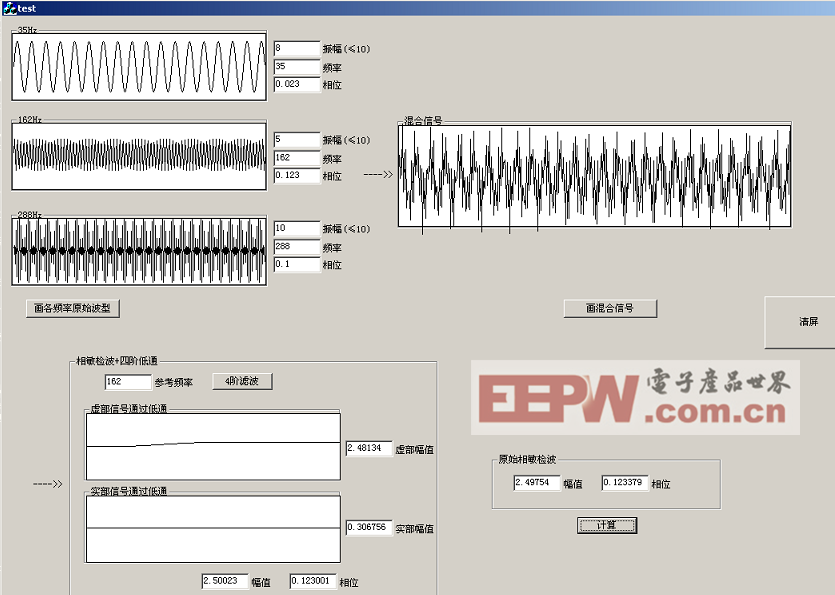
图6 数字相敏检波在VC++6.0上的测试结果

5  结论

本文所提出的基于低通滤波的数字相敏检波算法达到了更好的检波效果。通过理论分析与试验结果表明，改进后的算法在不同频率、相位、幅值等条件下，精度均比改进前有明显提高。

加入低通滤波后，会增加计算量。但是现在DSP处理器的计算能力已经比较强，加之ADC芯片信号采集速度也已经很快，因此改进后的算法在实际实现上将不是问题。这里所提出的算法将使得侧向仪器能够更加准确地获取数据，更加客观地反映地层电阻率情况。

参考文献：

[1]   张家田，梁亚萍，严正国. 基于数字相敏检波的三维感应测井信号处理方法研究[J]. 石油仪器，2009，23(6)：1.

[2]   黄家亮. 基于DSP的数字相敏检波器的实现[J]. 石油仪器，2009，12：2.

[3]   徐方友，肖宏，曹启刚，马雪青. 微电成像测井仪中数字相敏检波开方算法的改进及  DSP实现[J]，2011，4：2.

[4]   查普曼(Stephen J.Chapman). MATLAB编程[M]. 北京：科学出版社，2007：112-120.

[5]   余志强，刘建华，何朝峰，刘宁宁. 巴特沃兹数字滤波及其在智能测控系统中的应[J]，

     2007，5：3.

[6]   杨汉生，李明，杨成梧. 设计数字式巴特沃兹滤波器的新方法[J]，2006，4：2.

[7]   黄家亮. 基于DSP的数字相敏检波器的实现[J]，2009，12：6.

[8]   洪小丽，黄登红. 精密电感测微仪中的数字相敏检波技术研究[J]，2007，5：4.

[9]   刘升虎，邢亚敏. 精密电感测微仪中的数字相敏检波技术研究[J]，2008：5.

[10]  张家田，梁亚萍，严正国. 基于数字相敏检波的三维感应测井信号处理方法研究[J]，2009，6：3.

（注：本文来自于《电子产品世界》2020年11月刊）

关键词： 数字相敏检波 数字低通滤波

评论


相关推荐

技术专区

关闭