采集模拟信号：带宽、奈奎斯特定理和混叠

5. 计算上升时间

常量k取决于示波器。 大部分带宽不到1 GHz的示波器k值为0.35，而带宽大于1 GHz的示波器k值一般在0.4～0.45之间。

测量的理论上升时间Trm可以通过示波器的上升时间Tro和输入信号的实际上升时间Trs来计算得到。

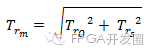
公式6. 计算测量的理论上升时间

建议示波器的上升时间为所测信号上升时间的1/3至1/5，从而以最小上升时间误差捕捉信号。

3. 采样率

采样率与带宽没有直接联系。 采样率是指ADC将模拟输入波形转换为数字数据的频率。 示波器是在经过模拟输入路径的衰减、增益和/或滤波后对信号进行采样的，并将所得到的波形转换为数字形式。 通过快照的方式进行，类似于影片的帧。 示波器采样速度越快，波形的分辨率和细节就越清晰。

奈奎斯特采样定理

奈奎斯特采样定理解释了采样率和所测信号频率之间的关系。 阐述了采样率fs必须大于被测信号感兴趣最高频率分量的两倍。 该频率通常被称为奈奎斯特频率fN。

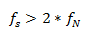
公式7. 采样率应大于奈奎斯特频率的两倍。

为更好理解其原因，让我们来看看不同速率测量的正弦波。 情况A，频率f的正弦波以同一频率采样。 这些采样标记在原始信号的左侧，在右侧构建时，信号错误地显示为恒定直流电压。 情况B，采样率是信号频率的两倍。 现在信号显示为三角波。 这种情况下，f等于奈奎斯特频率，这也是特定采样频率下为了避免混叠而允许的最高频率分量。 情况C，采样率是4f/3。此时奈奎斯特频率为：

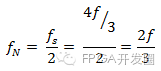
由于f大于奈奎斯特频率 )，该采样率再现错误频率和形状的混叠波形。

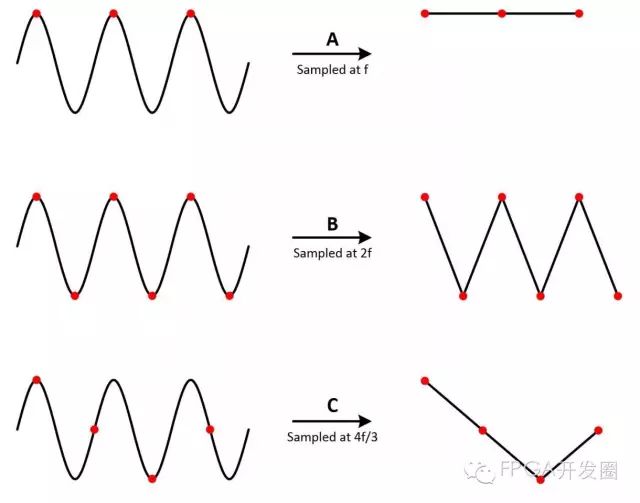
图6. 采样率过低会造成波形重构不准确。

因此，为了无失真地恢复原波形信号，采样率fs必须大于被测信号感兴趣最高频率分量的两倍。 通常希望采样率大于信号频率约五倍。

混叠

如需按一定速率采样以避免混叠，那么混叠到底是什么? 如果信号的采样率低于两倍奈奎斯特频率，采样数据中就会出现虚假的低频成分。 这种现象便称为混叠。 下图显示了800 kHz正弦波1 MS/s时的采样。虚线表示该采样率时记录的混叠信号。 800 kHz频率与通带混叠，错误地显示为200 kHz正弦波。

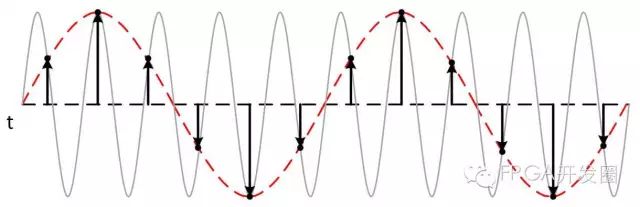
图7. 混叠发生在采样率过低的时候，产生不精确的波形显示。

通过计算混叠频率fa可确定输入信号超过奈奎斯特频率时的显示图。 混叠频率是指最接近采样率整数倍的频率和输入信号的频率之间的差的绝对值。

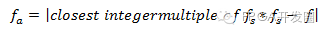
公式8. 计算混叠频率

例如，假设信号采样率为100 Hz，输入信号包含下列频率：25 Hz、70 Hz、160 Hz和510 Hz。 低于50 Hz奈奎斯特频率可正确采样;超过50 Hz的频率显示为混叠。

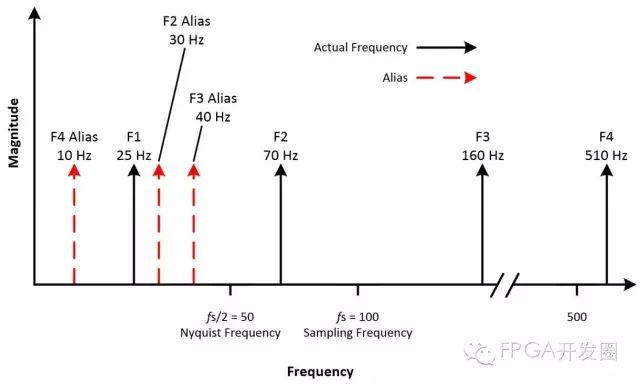
图8. 测量不同频率值，有些为混叠频率，有些为波形的实际频率。

混叠频率计算如下：

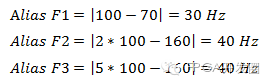
除增加采样率之外，使用抗混叠滤波器也可阻止发生混叠。 抗混叠滤波器为低通滤波器，可使输入信号中任何大于奈奎斯特频率的频率分量衰减，同时必须在ADC前使用以限制输入信号的带宽来满足采样标准。 模拟输入通道的硬件可包含同时采用模拟和数字滤波器来防止混叠。

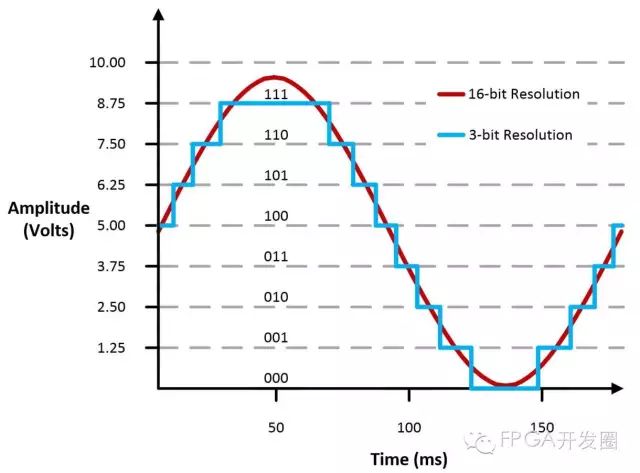
4. 分辨率

选择应用的示波器时需考虑的另一个因素是分辨率。 分辨率的位是指示波器可用来表示信号的幅值单元的数量。 理解分辨率概念的一种方式就是与码尺相比较。 将一个米尺分成毫米，分辨率是多少? 码尺上的最小计数单元就是分辨率：1/1,000。

ADC分辨率与最大信号可被分成的单元数量相关。 幅值分辨率由ADC具有的离散输出电平数量决定。 二进制码表示每个区间;这样，电平数计算如下：

公式9. 计算ADC的离散输出电平

例如，一个3位示波器有23或8个电平。 而一个16位示波器就有216或65,536个电平。 最小可检测的电压变化或码宽可计算如下：

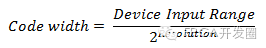
公式10. 计算码宽

码宽也称最低有效位(LSB)。 如设备输入范围是0～10 V，那么3位示波器的码宽为10/8 = 1.25 V，而16位示波器的码宽为10/65,536 = 305 μV。 由此可见显示的信号差别会非常大。