基于MUSIC算法的相干信号DOA估计改进及应用

　　I-MMUSIC算法可以由以下运算来实现：

　　1)阵元均匀分布的线性天线阵列(M个阵元)接收信源信号，如得到式(12)中的数据矢量X，接收的快拍数为N。

　　并且对N次快拍的矩阵求平均值，则可得到：

　　进行空间谱估计，可得到波达方向角。

5 I-MMUSIC算法应用于车载防撞雷达系统研究

5.1 系统实现算法分析及流程设计

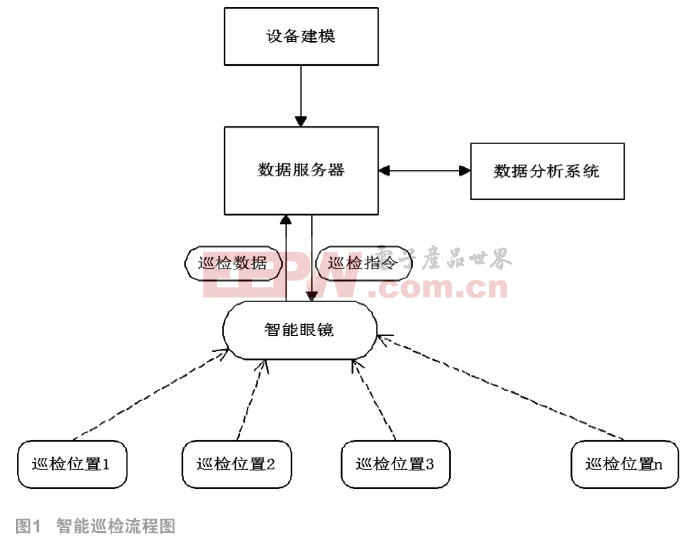
　　如图2所示，给出了防撞雷达系统实现流程。该流程主要由天线阵列接收模块、A/D采样及滤波模块、相位校正模块、距离估计模块和角度估计模块组成。

5.2 距离估计模块分析

　　1)系统测距原理分析及实现

　　首先从线性调频波雷达的测距原理进行说明。图3给出了雷达发射信号与回波信号的示意图。

　　在该雷达的设计中所采用的信号为线性调频连续波(LFM-CW)，雷达发射机端发射出线性频率连续波信号，该信号的特性参数可以设置成发射周期为T_m，频率初始值为f₀，扫频带宽为Δf。在理想情况下，电磁波经过障碍物反射回雷达接收机后，接收机接收的回波信号与发射机发出的信号具有相同的特性，二者的相异之处仅仅在于时间上的延迟。如图3所示，回波信号与发射信号的在时间上的延迟为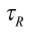，存在如下关系式:

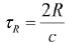(22)

　　式(22)中，R表示雷达与障碍物的距离差，c为空气中电磁波的传播速度。

　　如果发射机、目标物体和接收机三者之间相对静止，那么发射信号与回波信号之间的频差将为一个固定常量f_Δ，该频率差值与目标物体之间的距离成正比的关系，关系式如式(23)所示：

　　2)FFT变换

　　在该模块中，主要目的是获得A/D采样信号的频率值，将信号从时域到频域进行变换。目标物体与障碍物之间的距离与获得信号的频率存在线性关系，所以在信号处理过程中，如何获得成为需要解决的重要问题。为了得到明显的需要用傅里叶变换对A/D采样后的信号进行算法处理。

　　FFT对A/D采样后的数字信号数据进行处理，如果在FFT变换中使用的数据为复数，则对应的每个频点上包含了信号的距离和方位信息，可以对复数取模来获得信号的幅值。在此需要注意到，每个频点的相位就是该点的复数表示的相位，虽然经过了FFT变换，但是不影响这个频点的相位，对后续的信号处理无影响。

5.3 角度估计模块实现分解

　　角度估计模块的算法使用I-MMUSIC算法，该模块涉及到了大量复杂的数学运算，计算过程中的详细分解步骤如图4。

　　该模块是在进行完FFT运算后开始的。经过FFT运算后，目标信号的距离信息已知，再对每个频点在空域上进行数据采样，然后同时进行前向和后向的空间平滑运算，得到变换后的矢量矩阵，接着对它们分别同时进行协方差矢量运算。为了与后面的算法结合，需要将得到的前向和后向的空间平滑的协方差矢量矩阵按照式(24)进行计算得到融合后的矢量矩阵。并对它做特征值运算分解，获得该矩阵的特征值以及特征向量，此矢量中包含噪声和信号特征子空间。我们可以根据特征值等信息，然后使用MDL准则对信号源的数目进行判断，得到在单一频率上信源个数。在得到该频点上信号源个数的前提下，对上述得到信号矢量进行分解，分别得信号特征矢量和噪声的特征矢量，最后利用噪声信号矢量进行谱峰值搜索得到信源信号的能量信息，进而实现信号的波达方向角的估计。

6 算法实现仿真

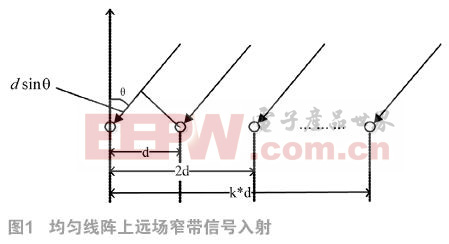
　　在仿真过程中，设置天线阵列为均匀等间距的线阵，阵元个数为14，两个阵元之间的间距为1.56cm，入射信号的波长设置为1.25cm。同时设定天线采样的快拍数为64，每次采样的点数为720点。在信号端加载的噪声为高斯白噪声，信噪比为20dB，噪声与信号源之间完全独立。

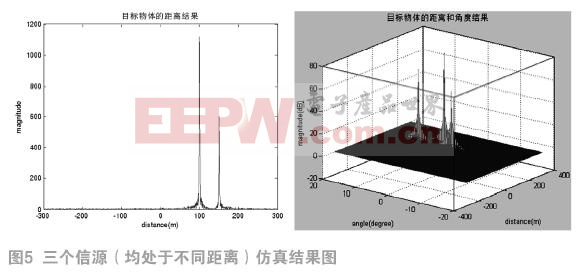
　　(1) 设定有信源数为3的独立窄带远场信号入射到天线阵列上，信源方向分别为0°、4°和10°，对应的天线与信源的距离为100m、150m、100m，此时，三个信源信号为相干信号。图5给出了目标物体的距离的二维仿真图像和最后生成的空间谱的仿真图像。

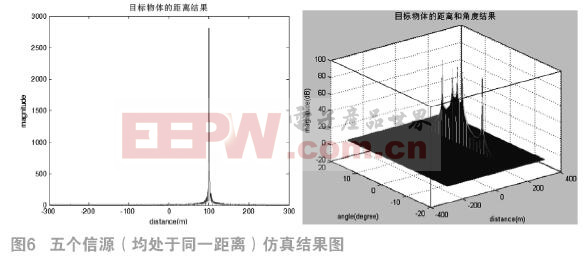
　　(2) 设定有信源数为5的独立窄带远场信号入射到天线阵列上，信源方向分别为0°、2°、 4°、8°和-8°，对应的天线与信源的距离均为100m，此时，这五个信源信号为相干信号。图6给出了目标物体的距离的二维仿真图像和最后生成的空间谱的仿真图像。

　　对以上仿真结果进行分析：在这两次仿真结果中，信源信号均为相干信号，其中第一次实验仿真的信源数为3，第二次的信源数为5，两次均能得到的针状空间谱图像的坐标均与预先设定参数相同，说明了该算法对于多信源相干信号的有效性。

参考文献：

　　[1]高琦.基于阵列信号处理的交通监测雷达实现[D].西安：西安电子科技大学,2015.

　　[2]张贤达,保铮.通信信号处理[M].北京:国防工业出版社, 2000.

　　[3]陈华.窄带阵列信号处理算法研究[D].天津:天津大学, 2012.

　　[4]张琦.基于时空二维MUSIC算法的DOA估计及其硬件实现方法研究[D].西安电子科技大学,2014.

　　[5]张小飞,汪飞,徐大专.阵列信号处理的理论和应用[M].北京:国防工业出版社, 2010.

　　[6]陈昊.空间谱估计算法的高速实现[D]. 成都: 电子科技大学, 2003.

　　[7]周丹凤.MUSIC算法及其并行实现[D].西安电子科技大学,2014.

　　[8]王永良,陈辉,彭应宁,等.空间谱估计理论与算法[M].北京:清华大学出版社, 2004.

　　[9]白玉.阵列信号处理中的DOA估计技术研究[D].哈尔滨:哈尔滨工程大学, 2006.

　　[10]I Reed, CL Nikias, VK Prasanna. Multidisciplinary Research on Advanced, High-Speed, Adaptive Signal Processing for Radar Sensors[J]. Final technical rept. 1996, 1: 155-159.

　　[11]Roman, J.R. Parametric adaptive matched filter for airborne radar applications[J].Aerospace and Electronic Systems, 2002, 36(22): 677 - 692.

　　[12]Frost, Victor S. A Model for Radar Images and Its Application to Adaptive Digital Filtering of Multiplicative Noise[J]. Pattern Analysis and Machine Intelligence,1982, 03:157-166.

　　[13]叶中付,沈凤麟.DOA估计中自相关矩阵的时空二维估计方法[J].信号处理,1995,11(3): 206-212.

　　[14]卞立军. 空间谱估计侧向系统设计[J]. 电子设计工程, 2009, 17(4): 91-94

　　[3]唐孝国,张建云,洪振清.一种改进的MVDR相干信源DOA估计算法[J].电子信息对抗技术, 2012,27(6):6-10.

　　[15]Panayirci, E. Multiple jamming suppression with minimum redundant antenna arrays for radar systems[C]. Edinburgh: Radar 97 (Conf. Publ. No. 449), 1997.

　　[16]吴娟.宽带信号的DOA估计超分辨算法研究[D].哈尔滨:哈尔滨工业大学, 2007.

　　[17]赵学伟.阵列误差对DOA估计的影响及校正[D].成都:电子科技大学, 2008.

　　[18]Krim H，Viberg M. Two decades of array signal processing research.IEEE Signal Process Magazine,1996,13(4):67-94

　　[19]Jao, J.K. Amplitude distribution of composite terrain radar clutter and the K-Distribution. Antennas and Propagation. IEEE Transactions on,1984, 3(10):1049-1062

　　[20]Capon J. High-resolution frequency-wavenumber spectrum analysis[J].Proc. Of IEEE, 1969,57(8): 1408-1418.

　　本文来源于《电子产品世界》2017年第5期第71页，欢迎您写论文时引用，并注明出处。