数字PID控制及其改进算法的应用
2 PID控制的改进算法
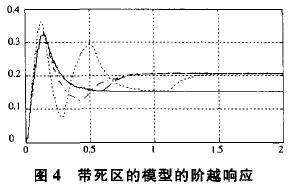
在理想的数学模型中加入大小为-0.25~0.25的Dead Zone(死区),如图3所示进行仿真,仿真实验结果如图4所示。仿真中为了更好的探讨积分环节的作用,取KD=0。图中Kp=3,实线无积分控制作用,可以看出有较大静差;点线为加入积分控制,并取KI=0.0015;分析可知:积分环节可以减小上升时间,但会增大超调量,延长调整时间。事实上,如果要减小上升时间,可以增大Kp的值,没有必要为了减小上升时间而加大KI的值。
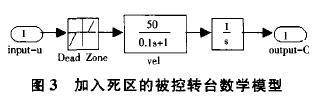
图4中虚线为采用积分分离PID控制的过程,可以看出积分分离PID算法明显改善了控制过程。积分分离PID算法的思想是在误差较小时保留积分控制作用,而在误差较大时取消积分控制环节。积分分离PID控制器在误差较大时保证系统的跟踪性能,而在误差较小则能保证系统稳态精度和抗干扰性能,较大的改善控制性能。
积分分离PID控制写成公式时,可在积分项乘一系数β,其值根据误差大小来决定。

其中:ε>0——设定的阈值。此时积分分离PID控制算式的积分控制写为:

积分分离PID算法的另一本质就是改变了过去的误差对控制量的权系数,而不再是普通的求和(普通的求和权系数相同,都是1)。同时我们可以用连续函数(连续或分段连续)来计算求和的权重,比如采用连续函数:
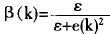
来计算权系数β(k),其中参数ε根据需要调整,当e(k)2=ε时,β(k)=0.5。此时,积分控制量写为:
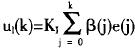
图4中的点画线为变速积分控制过程,其中ε=0.0015,KI=0.004。显然变速积分法要比积分分离算法效果要好,但是变速积分法要花费更大的代价来实现,而且积分分离算法效果不错,变速积分法只不过稍稍改善了一些性能。
根据各种改进积分环节算法的有效性和代价,我们选择容易实现而且效果不错的积分分离算法运用于我们实际的转台控制,得到了很好的控制效果。
3 结束语
根据对转台控制的仿真和经验,总结出PID参数工程整定的一般步骤:
只加入比例控制环节,慢慢增加Kp使系统微微振荡起来;
加入微分控制环节,慢慢增加KD,这相当于增大系统的阻尼,使系统平稳下来;
系统平稳下来后,再增加Kp使系统微微振荡起来,然后再增加KD使系统平稳下来,如此反复下去,直到Kp和KD都不能增加时为止;
再把Kp的值适当减小一点。加入积分控制环节,慢慢增加KI的值,直到稳态误差在可接受的范围内;⑤ 为了使系统更可靠和稳定,保证鲁棒性。最后还要把KP、KD、KI的值都适当减小,再根据经验做一些相应的调整。



评论