数字PID控制及其改进算法的应用
转台是检测和评价惯性导航与制导系统的主要测试设备。转台内安装的是力矩电机,因此理想的转台的数学模型可以写成直流力矩电机的数学模型,PID控制器各控制环节的作用是这样的,比例控制(P控制)即时成比例地反应控制系统的偏差信号e(t),积分控制(I控制)主要用于消除静差,微分控制(D控制)反应偏差信号的变化趋势(变化速率)。比例控制是对现在误差的一种校正,积分控制是对过去误差的校正,而微分控制是对将来可能的误差的校正。下面结合转台的控制过程对数字PID控制及其改进算法作具体的讨论。
1 Simulink仿真
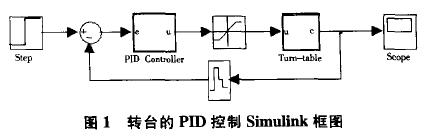
转台的PID控制的Simulink仿真框图如图1所示。其中包含了两个子系统PID Controller(PID控制器)和Turn-table(转台)。对理想模型进行Simulink仿真实验。选用不同参数的PID控制器,它们对幅值为0.2的参考输入的阶越响应的过程曲线如图2所示。图中实线为只采用比例控制,取Kp=1;点画线、虚线和粗线均为采用比例微分控制,点画线的KI=1,KD=200;虚线的Kp=1,KD=600;粗线的Kp=10,KD=1000;图中点线为PID控制,Kp=1,KI=0.0005,KD=200。
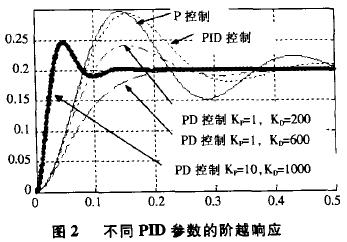
分析图2可得出:
① 对于理想的数学模型,不需要积分控制项,只采用PD控制就够了。由于积分控制项的目的只是消除静差,所以在系统没有静差的情况下不要加入积分控制环节,因为积分控制环节会恶化过程动态特性,造成过大的超调量,并增加了调整时间;
② 不要忽视微分控制环节。要减小上升时间,增加系统的控制刚度,必然要求增加Kp,但过大的Kp会产生过大的超调,甚至使系统振荡,但增加Kp的同时只要增加KD一般都可以减小超调,获得较好的动态特性。可以这么说,理想的数学模型,采用大参数的PD控制可以获得足够好的控制性能。但也不是说可以一味的增加KP和KD的值,因为KP值越大,控制量u也越大,消耗的能量也越多,而且u受饱和限制。
运用PD控制在实际转台系统中时,有较大的稳态输出误差,并且输出波动较大。分析原因如下:
① 由于功率放大器有较大的死区,而且转台的机械系统存在有静摩 擦力,使实际的被控系统有较大死区。所以控制器如果没有积分环节,稳态输出有较大的静差;
②实际的被控系统总是会受到许多干扰,包括各种不确定的系统噪声和量测噪声。过大的KD会放大噪声,使系统的输出波动较大。



评论