相位噪声和抖动的概念及其对系统性能的影响

如何将相位噪声转换为抖动

如前所述，抖动和相位噪声所描述的是同一现象的特征，因此，如果能从相位噪声的测量结果中导出抖动的值将是有意义的。以下介绍推导方法：每个振荡器都有其相位噪声图，图4给出一个例子。该图中绘出的是从12 kHz到 10 MHz这个频带范围内，某振荡器的相位噪声情况。图中，L(f)以功率谱密度函数的形式给出了边带噪声的分布，单位为dBc。中心频率的功率并不重要，因为抖动只反映了相位噪声(即调制)与“纯”中心频率处的相对功率值。边带的总噪声功率可以由L(f)函数在整个感兴趣频段内(在本例中，即12 KHz到 10 MHz频段内)积分得到。

计算得到的是相位调制噪声在该频段内的功率，而相位调制正是造成抖动的原因。由此，我们还能用如下的定积分推出RMS抖动的值。

下式可求得该噪声功率造成的RMS抖动：

抖动值还可以用其他单位表示，例如单位时间（UI）或时间。将上式除以以弧度为单位的中心频率就可以将抖动单位转换为时间，见下式：

利用图4所绘的噪声功率值，我们可以计算一个312.5MHz振荡器的RMS抖动。将相位噪声曲线在12 kHz到20 MHz范围内积分，得到-63 dBc：

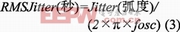
因此可以得到如下式所示的RMS相位抖动值，单位为弧度：

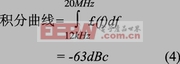
还可以将该抖动值单位转换为皮秒：

而同样的312.5 MHz振荡器的典性总抖动值在5ps RMS左右。

最终，我们计算得到的0.72 ps RMS的抖动值只在最大抖动中占很小的比例。