基于CPLD的温度自动控制系统的研制
温度自动控制系统的软件算法通常是根据对象的纯滞后时间τ与对象的惯性时间常数Tm之比来确定,一般来说,当τ/Tm0.5时,可采用PID算法控制,当τ/Tm>0.5时,可采用达林算法控制。在本系统中,针对不同的被控对象,可加载不同的软件算法,因此大大提高了本控制系统的灵活性。由于在工业控制过程中,大量的被控对象具有非线性、纯滞后性,采用PID控制很难获得良好的控制性能,因此本文重点讨论达林算法,用它来控制非线性、纯滞后对象具有良好的效果(被控对象一般为带有滞后的一阶惯性环节)。
2.1 dahlin算法的数学模型
被控对象为带有滞后的一阶惯性环节,其传递函数为
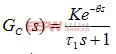
,θ=NT (2-1)
式中:τ1 -----对象的时间参数
θ -----对象的纯延迟时间,为了简化,设其为采样周期的整数倍,即N为正整数。
K -----对象放大系数
达林算法的设计目标是使整个闭环系统所期望的传递函数Φ(s),相当于一个延时环节和一个惯性环节相串联,即
Φ(s)=
,θ=NT (2-2)
如图6所示,根据控制理论易得到带有一阶惯性对象的达林算法的基本形式:
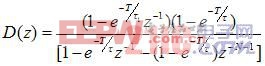
×
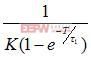
(2-3)
式中:K -----对象放大系数
T ------ 为采样周期;
τ1 ------为被控对象时间参数;
τ ------为闭环系统的时间参数。
根据D(Z)=U(Z)/E(Z)得出差分方程:
U(K)=b1U(K-1)+b2U(K-N-1)+a0E(K)-a1E(K-1) (2-4)
其中
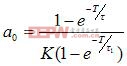
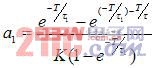
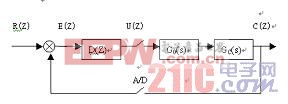
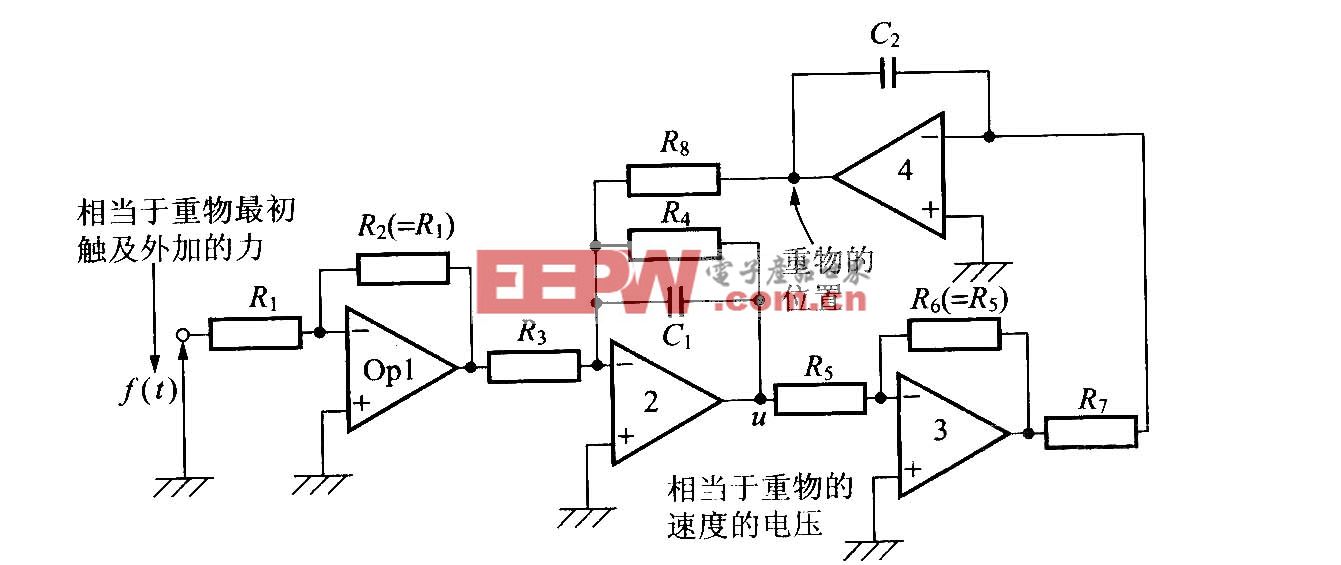
图6 控制系统方框图








评论