基于人脸识别的三维骨骼模型构造
加入技术交流群
1．2 测地距离的计算
人脸骨骼并不是一个刚性物体，它的某些部位(如下颌骨)会随表情的变化而发生变形。文献认为由于表情变化引起的人脸(骨骼)变形可以看作是一个等距(保长)的变换。这些变换并不拉伸与破坏面部骨骼曲面，或者更严格地说，它不改变面部骨骼曲面上的度量，因此人脸骨骼曲面的一些内在几何属性是与表情无关的。从而，为了得到人脸的一个表情无关的表示，也等价于寻找人脸骨骼曲面的一个等距表示。文献在人脸上放置了133个标记点，并且跟踪由于表情变化引起的这些点之间的距离变化。实验结果表明由于表情变化引起的测地距离的改变量不到欧氏距离改变量的1／2，当然对人脸骨骼的影响更小，几乎可以忽略不计。
在文献中，sethlan(1996)提出了一个高效的数值计算格式，称为Fast Marching Method(FMM)，它能够在O(N)步内计算一个平面上从一个源点到另外N个点的距离。FMM是基于求解短时矩方程(eikonal euqation)的迎风格式的差分逼近，短时矩方程是wave propagation equat-ion‖(x)=1 ‖的微分形式，其中v：
表示从源点s1，…，sk开始的距离映射函数，v(si)=O为上述方程的边界条件。
距离映射从源点出发，逐步向外传播。在文献中FMM被扩展到三角网格流形(TMTD)上。经典的FMM是在矩形网格上进行的，每次被更新的网格点都包含在—个直角三角形中。在三角网格流形的情形中，主要针对锐角三角形进行处理，如果要更新的网格点包含在一个钝角三角形中，文献提出了一个通过展开邻近三角片的方法来分裂钝角三角形。本文求解测地距离的方法基于文献。
1．3 测地模型
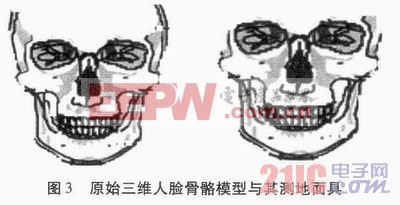
在前期处理阶段，我们需要提取三维人脸骨骼模型的面部区域。关键在于首先要在人脸骨骼上定位一个位置固定的源点，本文使用上一小节定位出的鼻尖点作为源点。其次需要找到在源点周围的一个等距(在测地距离意义下)区域。测地模型为该区域的内部，原始三维人脸骨骼模型中在该区域外面的点都被移除。这能保证我们在几何连续的意义下切割得到人脸骨骼的面部区域，同时由于采用测地距离度量，因此切割得到的人脸骨骼面部区域不受表情的影响。
测地模型是通过计算环绕三维人脸鼻尖点的一个区域而得到的，如图3所示。测地模型的半径是经验数据，是多次试验结果的总结，半径在80～110mm范围内波动，本文使用100毫米。我们使用Fast Marching Method来计算测地距离，切割之后得到的测地模型包含大约4 000～5 000个顶点。本文引用地址：https://www.eepw.com.cn/article/187556.htm
评论