基于达芬奇技术的三维全息显示系统研究
2.4 FFT运算
DSPLIB提供的FFT运算为基2的时间抽取算法。运算可以直接调用void cfft(DATA x,nx,shortscale)。其中:x[2*nx]为输入/输出数据存储数组;nx为FFT的运算长度;scale为归一化设置变量;scale=1是进行归一化设置变量,scale=0是不进行归一化运算。归一化功能使得输出结果被运算长度n所除,目的是为了防止FFT运算结果可能导致溢出。以一个简单的程序说明DSPLIB的使用。在该程序中输入数据放在x[512]数组中,运算后结果仍在x[512]数组中。

这样就完成了DSP内一个运算长度为256点的FFT变换。
3 结果分析
对频率为50 Hz的方波信号进行了频谱分析,采样点数为128,并调整采样频率,使得128点的采样时间为40 ms,即输入2个信号的周期。在通过DSP的集成开发环境(CCS)观看结果,如图3、图4所示。本文引用地址:https://www.eepw.com.cn/article/187429.htm


4 结语
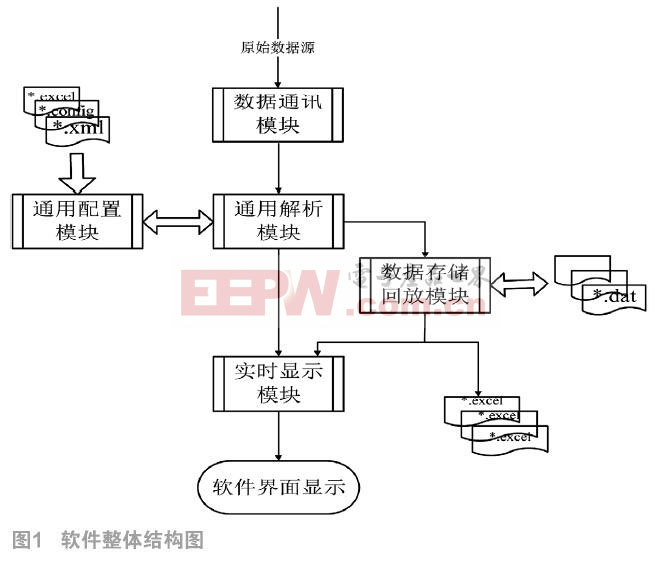
本文结合数字全息三维立体显示技术和达芬奇技术的优点,给出了一种全新的三维立体显示方案。结果显示,一个原始的图像数据经过该系统之后,从各个角度很完美地展现了原来的实物。因此该嵌入式系统平台具有很大的使用价值。





评论