开关磁阻电动机电流变幅斩波分析

2.2转矩波动分析

SRM低速运行时，为避免过大的电流脉冲峰值，多采用斩波限流工作方式，即在SRM一相通电周期内，斩波电流为唯一的幅值。图1所示为在传统斩波方式下，基于前述电机模型数值仿真计算的一台三相6/4极SRM电流及转矩合成情况波形，转矩波动主要产生在换流期间，此期间前一相绕组通电结束区和后一相绕组通电开始区输出转矩均较小。原因是对于三相6/4极SRM而言，相邻通电绕组相序为30°机械角，而一相绕组电感上升区为45°，绕组在电感上升区结束前应关断才不至于产生负转矩。在电感上升开始区和上升结束区电感变化率较小，而恰是在这两个区间电流处于上升和下降的过程，瞬时转矩值较小，因而转矩叠加区的值较小。所以合成转矩值也较小，产生了较大的转矩波动。图2是传统斩波方式下仿真计算的一台四相8/6极SRM的电流和输出转矩合成情况波形。可见对于四相电机来说，转矩叠加区的值较大。四相8/6极电机相邻通电绕组相序为15°，而每相电感上升区为30°，所以换流时后一通电相输出转矩与前一相输出转矩较大区叠加，因而，合成转矩较大，也使输出转矩产生了大的波动。

3变幅值斩波控制

3.1控制模型

鉴于以上分析，转矩波动主要是在换流期间相邻相输出转矩叠加而产生的。对于三相SRM而言，叠加区输出转矩值较小，而四相叠加区输出转矩值较大。因而可以通过改变叠加区相邻相的瞬时输出转矩值降低波动，也就是改变绕组导通开始区和结束区的电流，从而提出了变幅值电流斩波控制方式，即在绕组开始通电时斩波幅值设定一值，然后逐渐减小（对于三相SRM）或增大（对于四相SRM），在绕组通电中间区让斩波幅值恒定一段时间，然后再逐渐增加（三相SRM）或减小（四相SRM）到绕组关断。为此建立了电流斩波幅值Im的线性模型

Im0＋k(θ－θon)θonθθ1

Im=Im0＋k(θ1－θon)θ1θθ2（6）

Im0＋k(θ1－θon)－k(θ－θ2)θ2θθoff

式中：Im0表示初始设定斩波幅值；

k是系数，表示电流斩波幅值Im随角度θ的变化率，对于三相SRM，k取负值，四相SRM取正值；

θon,θoff分别表示相绕阻开通关断角；

θ1，θ2分别为恒定斩波幅值段起始角度与结束角度，依据不同电机结构取值。

3.2变幅值斩波控制对三相SRM的影响

基于上述电流斩波幅值控制模型，仿真计算分析了与图1传统斩波方式下SRM相同的电机结构参数，相同开通、关断角，相同平均输入电流情况下变幅值斩波控制电流及相应的合成转矩波形，如图3所示。仿真取k=0.007，θon=0.3°，θoff=33.6°，θ1=18.75°且θ2=26.4°。

对比图1与图3可以看出，相绕组通电开始区与通电结束区电磁转矩的提高，使换流期间合成转矩接近于电磁转矩较大的中间区，从而有效地降低了转矩波动。表1为对应图1的传统斩波方式及对应图3的

开关磁阻电动机电流变幅斩波分析

(a)相电流波形(b)相转矩及三相合成转矩

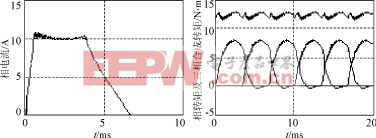
图3变幅值斩波方式下三相SRM

（注：图(b)中为清晰可见三相合成转矩为实际值加5N·m）

(a)相电流波形(b)相转矩及四相合成转矩

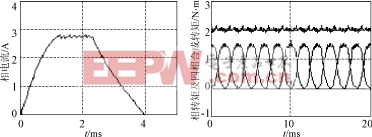
图4变幅值斩波方式下四相SRM

（注：图(b)中为清晰可见四相合成转矩为实际值加0.3N·m）

新型固态氧燃料电池

变幅值斩波方式下输入平均电流，输出平均转矩及转矩波动系数[7]表。由表1可知，变幅值斩波控制在并不降低转矩的情况下，大大降低了转矩波动。

表1三相SRM仿真结果IavTavk
传统斩波变幅值斩波6.43096.46797.29867.31280.27640.1781
3.3变幅值斩波控制对四相SRM的影响

图4为仿真计算的与图2相同条件下变幅值斩波时电流及相应的合成转矩波形图，仿真时k=0.03，θon=0.24°，θoff=25.2°，θ1=7.2°且θ2=20.4°。对比图2、图4，相绕组通电开始区与通电结束区相转矩的降低，使换流期间合成转矩接近于电磁转矩较小的中间区。表2为对应图2的传统斩波方式及对应图4的变幅值斩波方式，输入平均电流，输出平均转矩及转矩波动系数表。由表2可以看出，变幅值斩波控制大大降低了转矩波动，而且电感变化较大的中间段高的相电流使输出转矩有所增加。

表2四相SRM仿真结果IavTavk
传统斩波变幅值斩波1.53221.53221.31281.54320.45190.1447
4结语

开关磁阻电动机固有的转矩波动现象是电机振动和噪声产生的主要原因，所以实现SRM转矩波动最小化具有重要的意义。本文详细的仿真分析表明了针对不同相数采取的不同方式的变幅值斩波控制对降低SRM转矩波动的有效性。