交流调感稳压电源中等效电感的分析

uL=ULmsinωt（13）

式（12）与式（13）相等，当用有效值表示时，两边各除以电流有效值IL则得：(π－α＋sin2α)ωL=(π－α＋sin2α)ωLeLe=，（≤α≤π）（14）

文献（2）的计算结果为：Le′=，（≤α≤π）（15）

此式计算有两个错误：一是不应该用图3（b）的波形而应该用图3（d）的波形；二是图3（b)是镜对称，an≠0，a1≠0，所以文献2对式（15）的推导是错的，但可以用。

23三种等效电感计算式之间的关系

式（5）、式（14）、式（15）三种计算等效电感方程式之间的关系是：

式（14）表示的是Le与控制角α之间的关系，使用比较方便，故应用较普遍，式（5）在介绍稳压原理时使用方便，这两公式形式不同但实质是一样的。式（15）是不正确的，但可以用，在应用时必须要除2才能得到正确值。

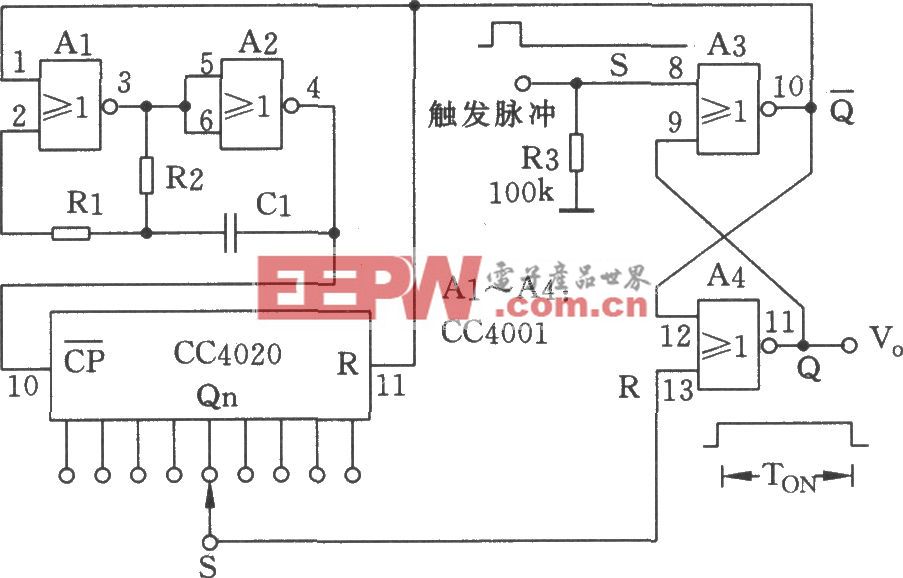
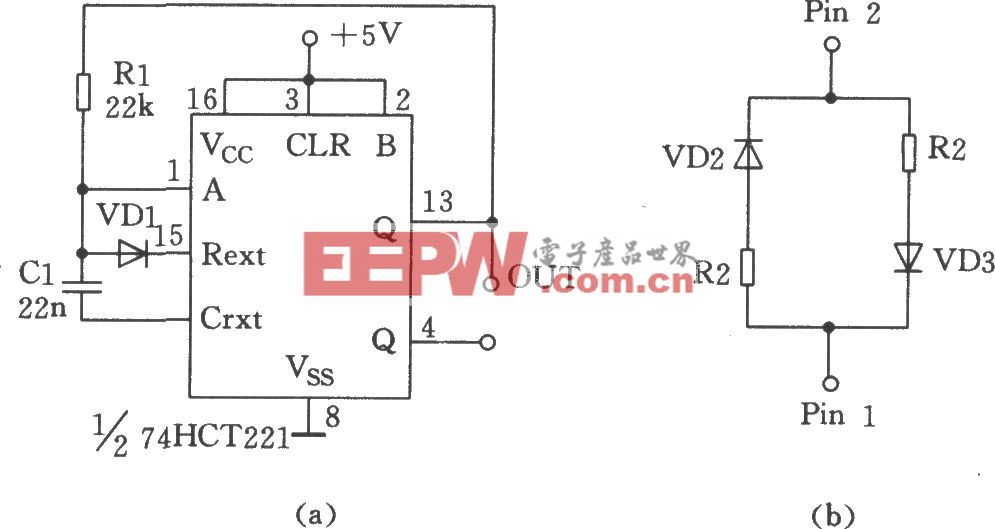
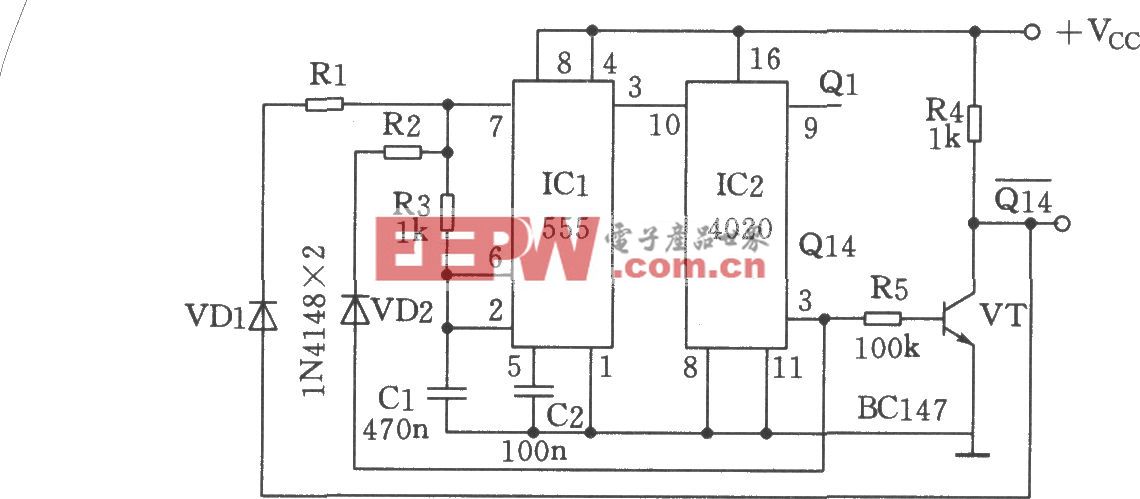
3高频PWM斩波器调感电路Le的计算高频PWM斩波器调感的等效电路如图4所示，斩波开关用IGBT和一个单相整流桥组成，由于工作于高频，所以采用了软开通和软关断缓冲电路，以减小IGBT的开关损耗。开关控制采用了EPWM直流等电位调制技术。触发脉冲的形成与交流电压PWM斩波波形如图5所示。为使波形半波奇对称和四分之一偶对称，以消除付里叶级数中的余弦项和偶次谐波，使载波比N==4K，K=1,2,3…，fc

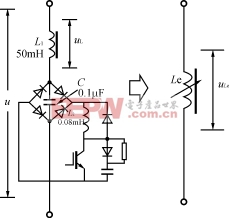
图4用高频PWM斩波器调感的等效电路

图5EPWM调制与正弦PWM斩波波形

为三角波频率，fs为市电工频；调制M=，Δt为脉冲宽度，TΔ=为三角波周期、Uc为三角波幅值、ΔU为输出电压的偏差、三角波电压的方程式为：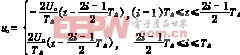

i=1,2,3…（16）

输出电压偏差ΔU为采样电压，触发脉冲起点ti和终点ti＋1的方程式为：脉冲宽度Δt=式中TΔ=，各触发脉冲的起点角和终点角的数值为：α1=(1－M);α2=(1＋M)α3=(3－M);α4=(3＋M)

由于PWM斩波波形是镜对称和原点对称，因此它的付里叶级数中将只包含正弦项中的奇次谐波，即：uL=bnsinnωtn为奇数bn=uLsinnωtd(ωt)=sinωt·sinnωtd(ωt)＋sinωt·sinnωtd(ωt)＋…）（17）

经计算，当n=KN±1时（K=1，2，3…）bn=KN±1=sinωt·sinnωtd(ωt)=－（18）

当n≠KN±1时，bn≠KN±1=0

对于基波，n=1b1=sin2ωtd(ωt)＋sin2ωtd(ωt)＋…）=sin2ωtd(ωt)=

=MUm（19）

uLe=MUmsinωt－sinKMπ·

sin(KN±1)ωt（20）由式（18）的谐波幅值sinKMπ可以算出：当fc=10kHz，N=200，M=0.1～0.9时，基波和各次谐波幅值与Um之比如表1所示，它们和调制比M的关系曲线如图6所示。可知，N越大谐波频率越高。当fc=50kHz，N=1000时用电路中L1=50mH，C=0.1μF就可以滤掉uLe中的所有高次谐波。

如求等效电感Le，由图4