LDO 噪声详解
图 8 对此进行了描述。CFF 值大于 100nF时,方程式 8 中1 + R1/R2 的放大器增益被抵销掉。出现这种情况的原因是,尽管低频噪声未被 CFF 完全抵销,但是低频噪声对 RMS 计算的总统计平均数影响不大。为了观察 CFF 的实际效果,我们必需查看噪声电压的实际频谱密度图(图9)。图9表明,CFF=10µF 曲线的噪声最小,但是某些频率以上时所有曲线均接近于这条最小噪声曲线。这些频率相当于由 R1 和 CFF 值决定的谐振极点频率。R1 等于 31.6 k 时计算得到的 CFF值,请参见表 2。
表 2 计算得谐振频率
CFF=10pF | CFF=1nF | CFF=100nF | CFF=10µF | |
fResonant | 504kHz | 504kHz | 504kHz | 504kHz |
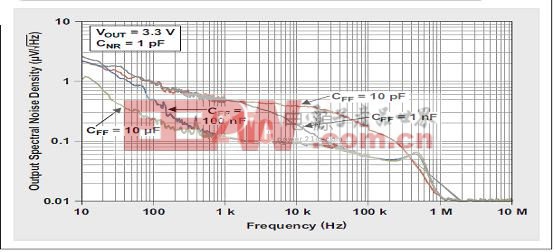
图 9 各种 CFF 值的输出频谱噪声密度
降噪 (NR) 引脚的效果
在 NR 引脚和接地之间使用 RC 滤波器电容(CNR)时,GRC 下降。图 10 表明 RMS 噪声为 CNR 的函数(参见图 5)。稍后,我们将在第三段“其它技术考虑因素”中说明这两条曲线的差异。
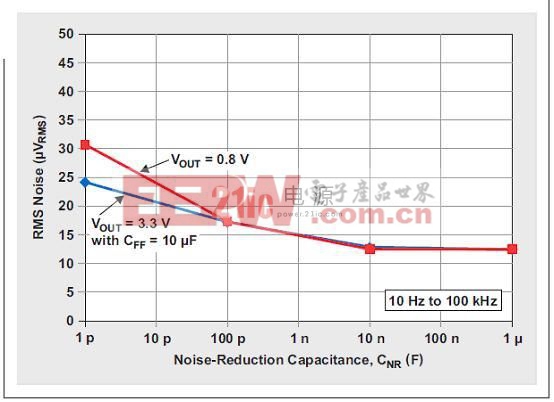
图 10 RMS 噪声与降噪电容的关系
图 10 利用 10 Hz 到 100 kHz 更宽融合范围,来捕捉低频区域的性能差异。CNR=1pF 时,两条曲线表现出非常高的RMS噪声值。尽管图 10 没有显示,但不管是否 CNR=1pF,都没有 RMS 噪声差异。这就是为什么在前面小节“放大参考噪声”中,我们把GRC被看作等于 1 的原因。
正如我们预计的那样,随着 CNR 增加,RMS 噪声下降,并在 CNR=1µF 时朝约12.5 µVRMS 的最小输出噪声汇聚。
CFF= 10 µF 时,放大器增益(1 + R1/R2)可以忽略不计。因此,方程式 8 可以简写为:
![]()
正如我们看到的那样,VN(Other) 并不受 CNR 影响。因此,CNR 保持 10.5 µVRMS,其由图 6 所示数据曲线拟合度决定。方程式 10 可以表示为:
![]()
接下来,我们要确定 GRC 降噪电容的影响,这一点很重要。图 10 中曲线的最小测量噪声,让我们可以将方程式10改写为:
![]()
其中,求解VN(REF) × GRC 得到 2 µVRMS。增加 CNR 会使参考噪声从19.5 µVRMS降至 2 µVRMS,也就是说,在 10 Hz 到 100 kHz 频率范围,GRC 从整数降至 0.1 (2/19.5) 平均数。






评论