RS(204,188)码连续编码的设计
在数字电视中RS码通常是以帧的形式来传输的,一帧又有八个数据包,因此连续编码就有特别的必要。编码时先输入51个是零的数据,得到编码后将前面51个数据丢弃。要得到RS(204,188)的编码先要得到域元素,可以借助MATLAB软件来获得。程序如下:m=8;%每个符号的比特数;n=2∧m- 1;%编码后码字长度;本文引用地址:https://www.eepw.com.cn/article/166871.htm
k=n-16;%信息长度;gfelement=gftuple([-1:n-1]',m)%产生加罗华域元素;
还可以来求生成多项式g(x).g(x)=(x+1)(x+a)…(x+a15)
程序如下:
N=255;k=239;b=0;gx=rsgenpoly(n,k,[],b)%[]表示缺省的本元多项式。
可以得到g(x):
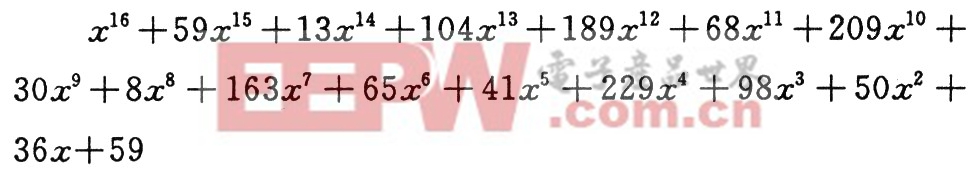
还可以输入一组数得到它的编码程序如下:
m=8;n=255;k=239;b=0;
genpoly=rsgenpoly(n,k,[],b);%产生生成多项式

code=rsenc(msg,n,k,genpoly)%信息码,前面51个为零,共239 bytes得到的校验码是:
48,168,46,159,119,162,72,132,139,235,172,28,76,175,171,238.
硬件设计时常用LFSR(线性反馈寄存器)来实现,可以图1表示。

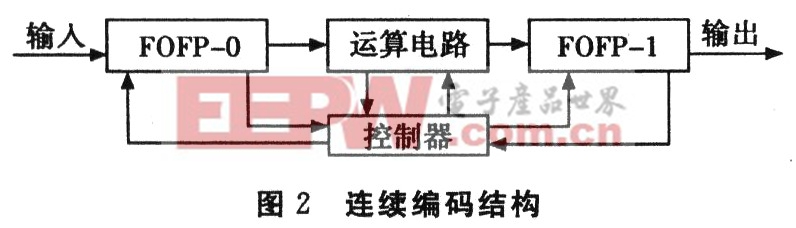
运算电路中主要运算是常系数的加罗瓦域乘法,假如有一个八位的二进制数:

域中的数相乘结果仍在域中,那就设结果为r(a)。则有
r(a)=b7a7+b6a6+b5a5+b4a4+b3a3+b2a2+b1a+b0。
与上式相比较就有:
b7=a6;b6=a5;b5=a4;b4=(a7+a3);
b3=(a7+a2);b2=(a7+a1);b1=a0;b0=a7;
同理可以得到编码需要的定系数伽罗瓦域乘法的结果。





评论