多电平变换器的拓扑结构和控制策略

2.3.3 载波相移PWM方法[12]

上面的两种载波方法，主要是针对二极管箝位型多电平变换器提出来的。而载波相移PWM方法则主要是用于级联型多电平变换器。这种方法与上两种方法不同，每一个级联模块的SPWM信号都是由一个三角载波和两个反相位的正弦波产生的。不过，相互级联的多个模块之间的三角载波有一个相位差θ。当θ=π/n（其中n为级联的模块的个数）时，输出相电压的THD最小。这种方法的原理和两电平中的倍频思想相似。

2.4 多电平的空间矢量PWM技术[13][14]

多电平空间矢量方法和两电平空间矢量方法一样，都是一种建立在空间矢量合成概念上的PWM方法。以三电平为例来说明多电平空间矢量多电平的原理，其空间矢量图如图8所示。为了减少谐波，被合成的空间矢量，一般都是用空间矢量定点落在的特定小三角形的三个定点的电压矢量予以合成。对于多电平变换器，用空间矢量合成的时候，计算比较复杂，很多文献讨论了不少简化的计算方法。另外，对于空间矢量，很多平衡中点电位的方法也被提了出来。空间矢量方法的特点是谐波小、电压利用率高，中点电位平衡容易实现。目前实用的一些多电平变换器大多数是用空间矢量PWM来实现的。

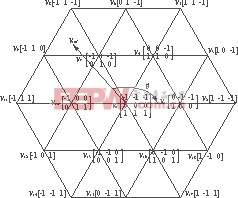
图8 三电平电压空间矢量图

2.5 多电平的Sigma-delta调制法(SDM)[15][16][17]

SDM是一种在离散脉冲调制系统(如直流谐振链逆变器)合成电压波形的技术。这一概念也是起源于两电平逆变器中，它的控制图如图9所示。图中V^＊为期望输出的电压波形，V为实际调制合成的输出波形。该控制部分中主要有三个环节，即误差的积分环节、量化环节、采样环节。该控制方法设计的主要任务就是设计合理的开关频率和积分环节的增益。一般定义G=K/f_s(式中：K为微积分环节的增益，f_s为开关频率),为了减少谐波，一般令0G1。图10为这种方法的调制波形。

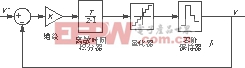
图9 SDM方法的控制框图

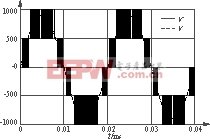
图10 五电平G=0.938，M=0.9时候SDM调制的波形

3 结语

本文介绍了多电平变换器的各种控制方法和各种拓扑，比较了其特点。从上面分析可以看到，各种拓扑结构和各种控制方法都有其特点，因此，在工程选择的时候，应合理予以选择。随着高速控制处理芯片DSP的出现，多电平变换器技术将会取得更广泛的实际应用。