三次样条插值在称重仪表误差补偿中的应用

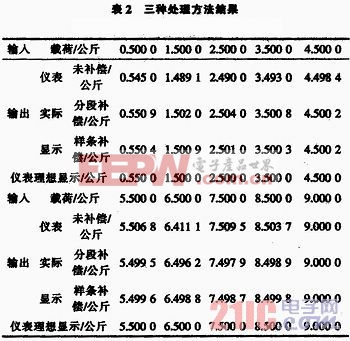
其中的分段线性补偿是目前仪表较为流行的一种误差补偿方法，其思想和三次样条插值误差补偿的思想基本一样，两者的差别是分段线性补偿在各个分段区间内进行线性计算，而三次样条插值误差补偿在各个分段区间内进行非线性计算。分段线性补偿处理方法相对简单，对传感器的非线性误差有一定的补偿作用，但对于高精度的数据采集系统该方法有时难以达到精度要求。
三种处理方法误差曲线分布如图3所示。

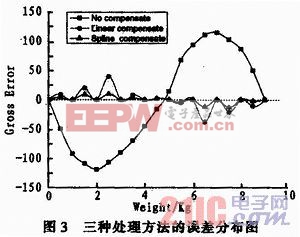
由表2和图3可得：
1)未补偿时，该仪表的满量程非线性误差为：119／90000=0．13％FS；其绝对误差在2 Kg处达到最大值119，在1 Kg处的相对误差达刭最大值0．8％；
2)采用分段线性补偿时，该仪表的满量程非线性误差为：40／90000=0.044％FS；其绝对误差在2．5 Kg处达到最大值40，0．5 Kg处的相对误差达到最大值0．18％；
3)采用三次样条插值补偿时，该仪表的满量程非线性误差为：13／90000=0．014％；其中绝对误差在7．5 Kg处达到最大值13，在0．5 Kg处达到相对误差最大值0．08％；

5 结论
通过三次祥条插值函数对仪表进行补偿可以得到较高的精度，满量程非线性误差、满量程内最大相对误差和最大误差都得到很好的改善，即使是传感器在低端呈现凹形特征和高端呈现凸形特征较为严重的情况下依然可以得到较高的精度，相比于分段线性补偿，其补偿的精度也大为提高。当插值点较少时，三次样条插值误差补偿的精度要比分段线性插值的误差要小得多。采用三次样条插值函效对仪表或其他的数据采集系统的误差进行补偿，除了可似很大程度上减少传感器非线性对精度的影响，还可以降低信号调理电路和AD转换器对系统精度的影响。
同时应注意到，对于有较高精度要求的数据采集系统，为获得较好的三次样条插值误差补偿效果，高精度的信号调理电路、AD转换器的稳定性是至关重要的。
另外适当选取插值节点数也非常关键，节点数选择过少，达不到较好的补偿效果，节点数过多不但造成计算量加大，还有可能造成在某些分段区间误差过大，从而达不到很好的补偿效果。一般的插值节点数选择在10～25个左右为宜。