跷跷板的模糊滑模控制系统设计

　　3模糊滑模控制器的设计

　　滑模变结构控制具有响应速度快、鲁棒性强等优点，被广泛应用与非线性系统控制当中，但是滑模控制容易引起系统的抖振现象，导致系统的最终不稳定。模糊滑模控制是在不确定环境下，对于复杂对象进行有效控制的一种智能控制方法。它不依赖系统的模型，而且对干扰具有完全的鲁棒性，同时保持了模糊控制和滑模控制的优点。模糊滑模控制的基本设计方法是在滑模控制系统的趋近阶段通过模糊逻辑调节控制作用来补偿未建模动力学的影响，其目的是提高控制系统的品质、减少到达滑动面时间、降低抖振。文中利用模糊控制规则调整控制输入量的大小，保证滑模控制到达条件得到满足。模糊滑模控制原理如图1所示。

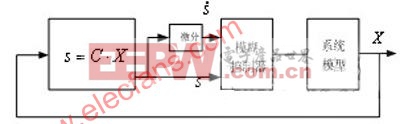
　　图1模糊滑模控制原理图

　　由图可知，模糊滑模控制系统由三部分组成，即切换函数、模糊控制器、和被控对象。滑模函数的输入为系统状态变量，切换函数设计为s=C·X

(1)

　　模糊控制器的输入为切换函数及其变化率，这样可有效的减少模糊规则的数量，很好的解决高阶系统多输入中存在的规则爆炸问题。控制的变化量作为滑模控制器的输出，可使模糊滑模控制成为无模型控制，依赖于被控对象的程度较小[7]。

　　根据模糊控制原理，定义模糊集，

　　其中PB，PM，PS，ZO，NS，NM，NB分别表示为正大，正中，正小，零，负小，负中，负大。在满足不等式的条件下设计，所获得的控制表如表1所示。使用的模糊规则是

　　表1模糊控制规则表

　　表中所有的控制规则是根据满足这个达到滑模的充要条件所设计的[8]，所以设计的模糊滑模控制系统是稳定的。

　　4仿真研究

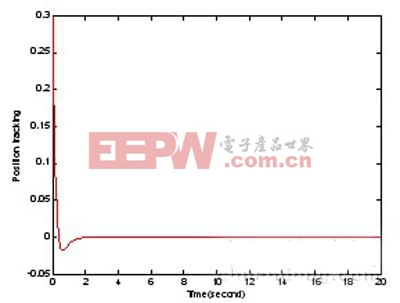
　　图2 小车位置随时间变化曲线