以谐波补偿为基础的逆变器波形控制技术研究

式中：k=0，1，…，N－1；

=。

显然，常规的FFT算法，其输出点数和输入点数是相等的，但在本系统中只须求出X(1)，X(3)，X(5)，X(7)，X(9)等5个输出点，其他输出点是不须计算的。根据基于FFT的蝶形计算流程图可以知道，在只须计算指定的若干个输出点的情况下，可以大大减少计算量，节省大量的DSP时钟，这就使得在计算能力并不强大的F240定点DSP上，实现基于FFT算法的实时频谱分析成为了可能。本文把这种经过化简的算法称为改进型FFT算法。

谐波发生器的作用是把FFT分析出的谐波进行预畸变，然后把预畸变的谐波信号作为补偿指令送给控制对象。之所以要对谐波进行预畸变，是因为控制对象对谐波的跟踪是有差的，这就导致谐波信号通过被控对象到达扰动注入点时，并不与扰动信号形状相同，而是相位正好相差180°的信号，这样就无法很好地抵消扰动。谐波发生器的预畸变算法表达式如下：

comp(n)=|X(n)|×modcoeff(n)×cos〔100πnt＋pha(n)＋phacoeff(n)〕（4）

comp=comp(n)n=1，3，5，7，9 (5)

式中：|X(n)|为谐波幅值；

pha(n)为谐波的初相位，它们由FFT算法计算得到；

modcoeff(n)为幅值补偿系数；

phacoeff(n)为相位补偿系数。

式(4)为单次谐波的补偿指令计算式，式(5)为系统需要补偿的所有谐波的总补偿指令计算式，它是各单次谐波补偿指令的简单累加。

幅值补偿系数modcoeff(n)和相位补偿系数phacoeff(n)可以通过控制对象的幅频、相频特性根据“等效逆”的原则简单地确定。具体来说，modcoeff(n)就是幅频特性频率对应点读数的倒数，phacoeff(n)就是相频特性频率对应点读数的负数。可以看出，谐波补偿器补偿系数的确定是非常简单的，这是本文所用控制方案的一大优点。

2 控制系统参数设计

2.1 FFT采样频率f_s和分析窗长度L的确定

采用FFT算法进行实时频谱分析，采样频率f_s和分析窗长度L的确定是非常重要的。假设所需要分析信号的最高频率为f_max。根据香农采样定律，只须满足

f_s≥2f_max (6)

就可以使被分析信号在频域中不产生混叠。在这里，基波是50Hz，最高只需要分析到9次谐波，所以f_max=450Hz。为了留有一定的裕量，在实际系统中f_s取1.6kHz。

分析窗长度L对于周期信号的频谱分析也是极其重要的，一般都把L取为被分析信号周期的整数倍，否则，会造成严重的频谱泄漏，大大降低频谱分析精度。显然，实际系统中被分析的误差电压信号周期就是基波周期，即为0.02s。所以就把L取为0.02s(即为周期的一倍)。

根据FFT的输入数据点数N的计算式：N=f_s×L，以及采样频率f_s和分析窗长度L的取值，可以得到N=32。这就是说，本控制系统须做32点的FFT。

2.2 幅值补偿系数和相位补偿系数的确定

在图2中，电压源U代表来自逆变桥的输出电压，电感L和电容C构成输出LC滤波器，电流源I代表负载汲取的电流，与滤波电感L串联的电阻r是滤波电感的等效串联电阻。由图2可知，在把逆变桥看作一个比例环节的情况下，逆变器的数学模型就是由输出LC滤波器构成的二阶系统。在本系统中，L=0.552mH，r=0.3Ω，C=135μF，所以逆变器数学模型为

G₁(s)= (7)

它的离散化表达式为

G₁(z)= (8)

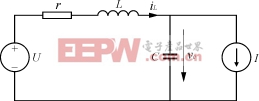
图2 逆变器等效电路模型