雷达成像近似二维模型及其超分辨算法
加入技术交流群
从式(12)可以看出：
是Zk归一化的二维离散傅里叶变换在{ωk,
k}处的值，所以只要得到估计值{
k,
k,
k,
k}，即可通过2D-FFT获得k.
将估计值k代入式(11)后，估计值{k,k,k,k}可由下式寻优得到：
(13)
由上式可见，对于固定的{μk,vk}取值,估计值{k,k}为归一化的周期图|aHM(ωk)Zkb*N(k)|2/(MN)主峰处的二维频率值.这样，式(13)的优化问题归结为：在(μk,vk)平面上可能的取值范围内寻找一点{k,k}，在该点处周期图|aHM(ωk)Zkb*N(k)|2/(MN)的主峰值比其余各点处的主峰值都大.所以，我们通过上述二维寻优获得{μk,vk}的估计值{k,k}，再由式(13)得到{ωk,k}的估计值{k,k}.
实际中，为了加快运算速度，二维(μk,vk)平面的寻优可以用Matlab中的函数Fmin()实现.
在做了以上的准备工作以后，基于推广的RELAX算法的参量估计步骤如下：
第一步：假设信号数K=1,分别利用式(13)和式(12)计算
1.
第二步(2)：假设信号数K=2，首先将第一步计算所得到的1代入式(8)求出Y2，再利用式(13)和式(12)计算2；将计算的2代入式(8)求出Y1，然后利用式(13)和式(12)重新计算1，这个过程反复叠代，直至收敛.
第三步:假设信号数K=3,首先将第二步计算所得到的1和2代入式(8)求出Y3，再利用式(13)和式(12)计算3；将计算的3和2代入式(8)求出Y1，然后利用式(13)和式(12)重新计算1；将计算的1和3代入式(8)求出Y2，然后利用式(13)和式(12)重新计算2，这个过程反复叠代，直至收敛.
剩余步骤：令K=K+1,上述步骤持续进行，直到K等于待估计信号数.
上述过程中的收敛判据与RELAX算法的收敛判据相同，即比较代价函数C1在两次叠代过程中的变化值，如果这个变换值小于某个值，如ε=10-3，则认为过程收敛.
四、数值模拟
1.算法参数估计性能模拟
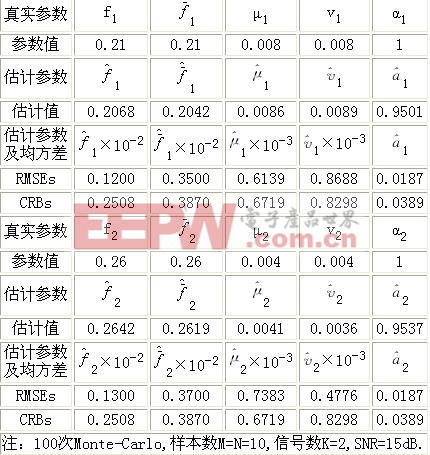
模拟数据由式（5）产生，M=10,N=10，信号数K=2.信号参数和实验条件如表1所示,为复高斯白噪声.注意两信号的频率差小于FFT的分辨率Δf=Δω/(2π)=0.1.表1给出了信号参数估计均方根误差的统计结果及相应情形时的C-R界，可见，估计均方根误差与CR界十分接近.另外表中还给出了估计均值，与真实值也非常接近.
表1 二维信号的参数估计、CRB及与均方根差的比较
评论