光电通信吊舱内框架悬置系统设计与分析
(4)在隔振器的支点布置质心与内框架的几何中心重合的基础上,如果能满足如下条件,则支撑系统的振动状态将实现进一步解耦。
此时除三个平动方向上的运动解耦外,绕x轴的激励与响应也将实现解耦,而其他两个转动自由度仍处于双联耦合关系。
将实现隔振系统六个自由度方向的激励与其对应振型响应完全解耦。
3 解耦设计
通过以上分析得知,当坐标系原点选在内框架质心处,质心与几何中心重合,并且隔振器支点相对质心对称布置的情况下,内框架振动系统能够实现完全解耦。结合内框架系统的实际情况,内框架的结构应设计得紧凑,整体外形尽量规则,便于对准几何中心。在内框架内当负载平台上的光学设备工作时相当于移动质量,这就导致内框架质心位置的变化,在设计光电平台时,应尽量将大质量或大转动惯量的仪器设备配置在内框架的质心附近,这样可以减小质心位置的变化,降低耦合程度,或者在相应位置配置相应的“配重”,用来平衡运动设备产生的质心偏移。
在合理选择支撑方案的基础上,还可以使用特殊结构的隔振器使系统进一步解耦。
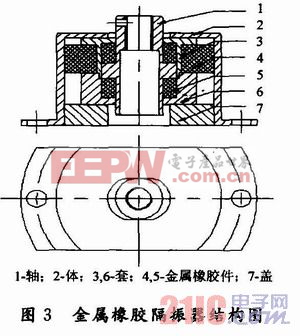
金属橡胶是一种均质的弹性多孔材料,其内部结构是金属丝之间相互嵌合、勾联而形成的类似于橡胶分子结构的空间网状结构。由于金属橡胶材料具有耐高温、高压、高真空、超低温,抗辐射,抗腐蚀,不易老化,阻尼大的优点,故设计了一种新型金属橡胶隔振器结构,如图3所示。金属橡胶隔振器能限制线振动转化为角振动,同时使外界传来的角振动转化为线振动。这种金属橡胶隔振器通过限制载体运动自由度的方式,使内框架振动系统消除了耦合。本文引用地址:https://www.eepw.com.cn/article/156373.htm
4 能量法验证
根据式(1)的动力学方程,可以求出系统固有频率及振型,在固定坐标系中,根据质量矩阵M和振型φi,可以求出系统在作各阶固有振动时的能量分布,将它写成矩阵的形式,定义为能量分布矩阵。
当系统作i阶主振动时的最大动能为:

在第k个自由度上,η在各阶振动中的最大值即为自由度k上的振动解耦率。如果η=100%,表示悬置系统作第i阶主振动时能量全部集中在第k个自由度上,即这个自由度相对其他的自由度解耦。
耦合的存在,使得一个广义坐标上的振动,会引起其余广义坐标的振动。能量法是在得到悬置系统的6个固有模态后,利用振型得到悬置系统的能量分布,根据能量分布判断动力总成悬置系统是否解耦或其解耦的程度,然后通过修改悬置参数提高系统在某方向上的解耦率。







评论