光电通信吊舱内框架悬置系统设计与分析
将八个隔振器布置在内框架两侧,每侧四个。与弹性系统相比,可将内框架系统视为刚体。隔振器为三向刚度隔振器,设隔振器位置坐标为(xi,yi,zi),沿三个坐标轴方向具有刚度kxi,kyi,kzi和阻尼cxi,cyi,czi(i=1,2,…,8)。如图2所示,以刚体内任意一点。为原点,建立惯性坐标系o-xyz。设内框架质量为m质心坐标为(,各轴的惯性矩为Ix,Iy,Iz,惯性积为Ixyk,Iyz,Izx。本文引用地址:https://www.eepw.com.cn/article/156373.htm
系统的动力学方程为:
![]()
式中:M,K,C分别为质量矩阵、刚度矩阵和阻尼矩阵。
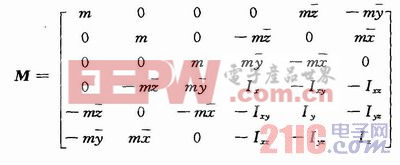

阻尼器与弹簧并联,故阻尼矩阵C与刚度矩阵K结构形式相同,也为对称矩阵。
F为基础激励列阵:
![]()
X为内框架绝对位移列阵:
![]()
U为基座(外框架)绝对位移列阵:
![]()
2.2 耦合分析
可以发现,质量矩阵、刚度矩阵和阻尼矩阵均为非对角矩阵,即系统存在着惯性耦合和弹性耦合。由于隔振系统通常采用相同的隔振器,即各隔振器对应方向的刚度和阻尼系数相等,故在分析内框架隔振系统的耦合情况时,假设各隔振器对应的刚度和阻尼系数相等。
从质量矩阵可以看出,当以内框架的质心为原点建立坐标系,并且坐标系各轴与内框架的主惯性坐标轴重合时,系统可以实现惯性解耦。即:

(1)假设内框架存在一个对称面xoy,将隔振器支点关于xoy,平面对称布置,即:

这样虽然使刚度矩阵结构变得简单,但仍然存在着一定的耦合。所以,只关于一个对称面布置隔振器不能实现解耦。
(2)假设内框架存在两个对称面,以隔振器关于xoy面和yoz面布置为例,即:

由刚度矩阵可知,此时系统y向运动实现解耦,x向运动与绕z轴转动、z向运动与绕x轴转动仍处于双联耦合状态。此外,绕x轴、y轴、z轴的转动状态方程也处于多联耦合关系。所以,关于两个对称面布置隔振器时只能实现一个平动自由度的解耦。
(3)假设内框架存在三个对称面,即将隔振器相对内框架几何中心对称布置,即:

由刚度矩阵可知,x向、y向、z向运动实现了完全解耦,但是绕三个坐标轴的转动仍处于多联耦合关系。







评论