采用卷积调制与间歇采样的多假目标干扰方法
因此,干扰信号频谱是原雷达信号的周期加权延拓,加权系数为an=τfssinc(πnfsτ)。当n=0时,即为原信号频谱。因此该分量经匹配滤波后会在雷达脉冲结束时刻形成与真实目标波形完全相同的主假目标,其幅度为τfs1,称为采样占空比。而其他分量X(f±nfs)发生了±nfs的频移,可以看成是附加了±nfs砸的频移干扰信号。若雷达信号为线性调频信号,利用线性调频信号频移和时延之间的强耦合性,经过脉冲压缩网络后,在时域上就会形成多个径向分布的不同幅度的假目标,且以主假目标为中心对称分布。但是随n逐渐增大,频移分量X(f±nfs)经过匹配滤波后的失配越严重,输出脉冲宽度逐渐展宽,且其幅度也不断降低。因此,间歇采样直接转发干扰一般最多只能产生3~5个有效的假目标干扰。本文引用地址:https://www.eepw.com.cn/article/153781.htm
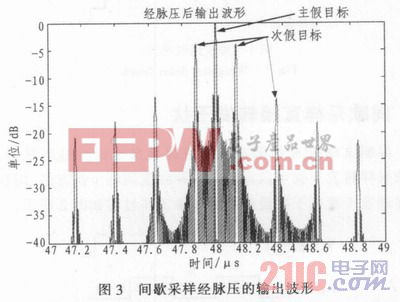
如图3所示,雷达信号带宽为100M,脉宽为48 μs,τ=3μs,Ts=6μs。一种特殊的情况是,fs=1/Ts大于信号带宽,则所有频移分量X(f± nfs)(n≠0)均位于雷达匹配滤波带宽之外,此时,干扰信号表现为一个主假目标干扰。这是该干扰样式的局限性。
3 卷积调制与间歇采样联合干扰分析
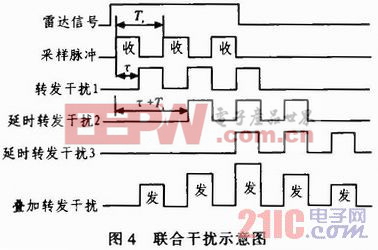
文中提出的联合干扰方式可以根据需要产生所需的假目标数目。其工作过程如图4所示。其思想是利用卷积调制干扰能产生数目不受限制的假目标的性质,同时利用间歇采样在特定干扰平台(机载、弹载)的工程可实现性。
根据式(1)和式(5),可得联合干扰信号为:
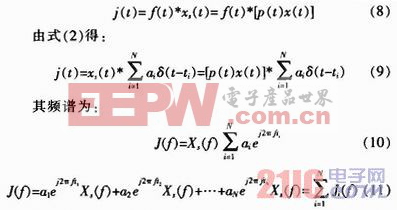
其中![]() 。假设干扰信号Xs(f)经匹配滤波后的时域脉压信号为ys(t),的首个主假目标出现在T时刻,即ys(t)的主峰值出现雷达脉冲结束时刻。根据傅里叶变换性质,Ji(f)经过匹配滤波后所形成的主假目标在时间轴上比首个主假目标滞后ti。因此J(f)经匹配滤波后总体效果可以表示为
。假设干扰信号Xs(f)经匹配滤波后的时域脉压信号为ys(t),的首个主假目标出现在T时刻,即ys(t)的主峰值出现雷达脉冲结束时刻。根据傅里叶变换性质,Ji(f)经过匹配滤波后所形成的主假目标在时间轴上比首个主假目标滞后ti。因此J(f)经匹配滤波后总体效果可以表示为
y(t)=a1ys(t-t1)+a2ys(t-t2)+···+aNys(t-tN) (12)
根据上节的讨论,该式表示形成的主假目标个数为N,同时每个主假目标周围分布着幅度较小的次假目标。
工程实现上,根据均匀间歇采样特性,合理选择延迟时间,如图4所示,t1=τ,ti=τ+(i*m-1)Ts,动态改变采样脉冲宽度τ和采样脉冲周期Ts,可以实现假目标的动态分布。
合理选择N值,可以实现在整个雷达脉冲重复周期内均有假目标出现,实现假目标的大范围空间分布。例如,脉冲重频为1ms,Ts=2 μs,则在1ms内最多可出现500个主假目标。当然实现这个目标还需考虑工程实现的可能性。同时,当ti>T,即雷达脉冲结束时,可令ti=τ+(j*m-1)Ts+△τ,改变△τ,m,可实现主假目标的非均匀分布。
4 对线性调频信号的干扰仿真
根据图4及式(12),设N=3,τ=1 μs,Ts=2μs,雷达脉冲宽度48μs,带宽为100 M,加权系数全为1。仿真结果如图5所示。
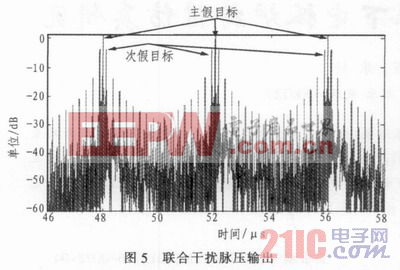
从图5中可以看到,第一个主假目标出现在48μs时刻,即脉冲结束时刻,其余两个主假目标分别出现在50μs和52μs时刻。主假目标间距为间歇采样周期。仿真结果与上节分析一致。






评论