雷达成像近似二维模型及其超分辨算法简述

式(4)与式(3)相比较，指数中增加了两项，其中前一项是“多普勒移动”项，纵坐标yk越大，影响也越大，这可以补充式(3)之不足;而后项是时频耦合的多普勒移动项，由于Mγ/Fs

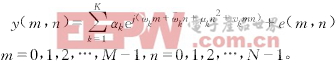
　(5)

需要指出，每个散射点的参数之间存在下述关系：ωk/μk=2γ/Fsfcδθ2和

k/vk=fcFs/γδθ.由于雷达参数(fc,γ,Fs)和运动参数(δθ)均已知，所以待估计的五个参数中只有三个是独立的.本文假设五个参数是独立的，而在成像计算中已考虑参数之间的关系.

设{ξk}Kk=1≡{αk,ωk,

k,μk,vk}Kk=1，现在我们要从y(m,n)中估计参量{ξk}Kk=1.

三、二维推广的RELAX算法

对于(5)式所示的信号模型，令：

Y=[y(m,n)]M×N

则

　(6)

式中

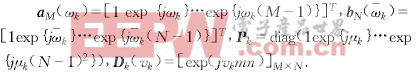
设ξk估计值为

，则ξk的估计问题可通过优化下述代价函数解决：

　(7)

式中‖.‖F表示矩阵的Frobenius范数，⊙表示矩阵的Hadamard积.

上式中C1的最优化是一个多维空间的寻优问题，十分复杂.本文将RELAX[3]算法推广以求解.为此，首先做以下准备工作，令：

　(8)

即假定{

i}i=1,2,…,K,i≠k已经求出，则式(7)C1的极小化等效于下式的极小化：

C2(ξk)=‖Yk-αk(aM(ωk)bTN(

k)Pk)⊙Dk(vk)‖2F　(9)

令：　　Zk=YkP-1k⊙Dk(-vk)　(10)

由于Pk为酉矩阵，矩阵Dk的每个元素的模|Dk(m,n)|=1,显然矩阵Yk与Zk的F范数相同，故C2的极小化等效于下式的极小化：

C3=‖Zk-αkaM(ωk)bTN(

k)‖2F　(11)

对上式关于αk求极小值就获得αk的估计值

k：

k=aHM(ωk)Zkb*N(

k)/(MN)　(12)