∑-△模数转换器工作原理及简单分析
加入技术交流群
2 ∑-△调制器的原理
2．1 过采样技术
过采样是使用远大于奈奎斯特采样频率的频率对输入信号进行采样。设系统原来的采样频率为fa，现在以远大于原来采样频率的频率即以N×fa的频率进行采样，其中，N>1，此时开始分布在0～fa／2频带内的量化噪声分布到0～Nxfa的频带内，即量化噪声的频谱分布发生了变化，当N>>1时，量化噪声在系统的频带之内的量化噪声就会减少，这就是过采样技术。补充一下系统的信噪比。信噪比即信号功率与噪声功率的比值，
由此式可以看出，信号功率
越大，信噪比越高，另一方面，随着字长b的增加，信噪比增大，且有A／D变换器的字长b每增加一位，信噪比增加约6 dB。为了改善SNR和更为精确地再现输入信号，对于传统A／D转换器来讲，必须增加位数。将采样频率提高一个过采样系数N，即采样频率为Nxfa，再来讨论同样的问题。此时，大部分噪声位于数字滤波器带宽之外而被滤除。已知一个1位A／D转换器的SNR为7．78 dB，每2倍过采样可以使SNR增加3 dB，则SNR每增加3 dB等效于分辨率增加0．5 bit。这样通过提高过采样率，时间来换取精度，从而使高精度的A／D转换器的电路简单化。但是单单采用过采样技术是不行的，例如采用1位A／D转换器进行256倍(即28倍)过采样可以获得5位分辨率，而要获得20位分辨率就必须进行238倍过采样，这是不切实际的。∑-△A／D转换器采用噪声成形技术消除了这种局限，使得每2倍过采样可增加高于3 dB的SNR。2．2 噪声整形原理
量化噪声是影响转换器精度的最主要的原因，如上述所说仅采用过采样技术还不能满足∑-△A／D转换器对结果精确度的要求，为了降低量化噪声对结果的影响，所以人们又采用了噪声整型原理，利用反馈克服过高取样所造成的技术困难并且使量化噪声在低频频带内分布的更少。再者，由于数字滤波器在工作过程中由于移位等也会生成一部分噪声，噪声整形就可以很好地解决这一问题，噪声整形处理再量化噪声，低频频带内的噪声将会大大减少，大部分的量化噪声就被推向更高的频段，这样在∑-△调制器后加入低通滤波器，就可以有效地滤除信号带宽外的量化噪声，大大提高了系统性能。与前面的简单过采样相比，总的噪声功率虽未改变，但噪声的分布发生了变化。在∑-△调制器中采用更多的积分与求和环节，可以提供更高阶数的量化噪声成形。
2．3 一阶噪声成型原理
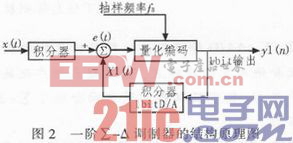
图2为一阶∑-△调制器的结构原理图，分析此结构可以得到以下方程：
y(kT)=x(kT-T)+e(kT)-e(kT-T) (3)
e(kT)=q(kT)-u(kT) (4)
对式(3)(4)进行Z变换得到一阶调制器的传输函数为：
Y(z)=Z-1X(Z)+(1-Z-1)E(Z) (5)
这表示一阶调制器的输入信号的一个采样时钟延迟和量化误差的一阶差分。本文引用地址：https://www.eepw.com.cn/article/153454.htm
2．4 二阶噪声成型原理
图3显示二阶∑-△调制器结构原理。2次噪声整形电路是进行2次低频提升和低频衰减的电路，即在∑-△调制方式1 bit量化器的前后，分别加2级积分器和微分器构成的，如同1次噪声整形简化方式一样，2次噪声整形使噪声分布斜率更加陡峭，低频区量化噪声得到进一步降低。
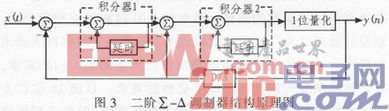
根据线性模型可推出二级∑-△调制器的方程为
y(kT)=x(kT-2T)+e(kT)-2e(kT-T)+e(kT-2T) (6)
经过Z变换可得
Y(z)=Z-2(Z)+(1-Z-1)2E(Z) (7)
可以看出由一阶调制器的级联而得到的二阶调制器的输出包括输入信号的2个采样周期延迟和量化误差的2阶差分。
模数转换器相关文章:模数转换器工作原理
低通滤波器相关文章:低通滤波器原理
电源滤波器相关文章:电源滤波器原理
数字滤波器相关文章:数字滤波器原理
评论