8/20浪涌测试波形时域转频域的解释及仿真思路（基于Python）

1.引言

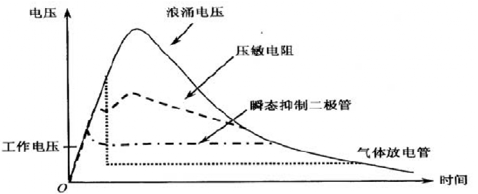
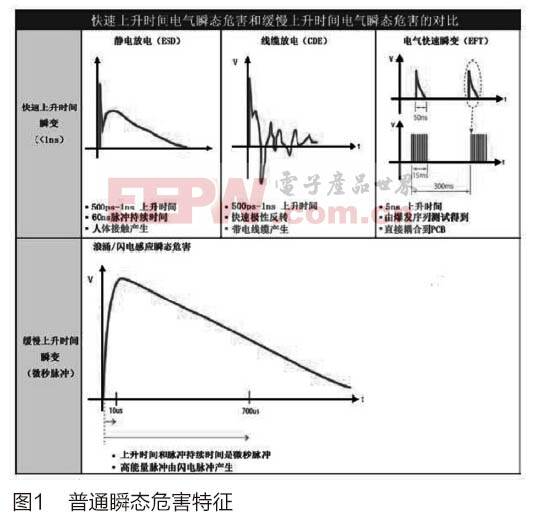
在电子工程和电磁兼容性（EMC）领域，8/20μs浪涌波形是一种标准的感应雷，常用于模拟雷电引起的瞬态过电流。这个波形因其陡峭的上升沿（8μs）和较长的下降沿（20μs）而得名，能够很好地模拟雷电冲击对电子设备的影响。今天，我将带领大家一步步了解如何通过仿真分析8/20μs浪涌波形的时域特性，并将其转换到频域进行分析，揭示其频率成分。2.时域分析

2.1 8/20μs浪涌波形的定义

8/20μs浪涌波形是一种典型的双指数脉冲波形，其数学表达式可以表示为：

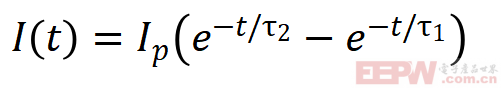
其中：

这个公式看起来有点复杂，但其实就是在两个指数函数之间做差，从而得到一个脉冲波形。简单来说，就是用一个快速下降的指数函数减去一个更慢下降的指数函数，形成一个快速上升、缓慢下降的脉冲。

2.2仿真生成时域波形

在代码中，`generate_8_20_waveform`函数通过上述公式生成8/20μs浪涌波形。具体步骤如下：

1.使用`np.linspace`生成时间数组`time`，表示仿真时间范围。

2.计算电流波形`current`，使用双指数函数模拟上升沿和下降沿。

3.对波形进行归一化处理，确保峰值电流为4kA。

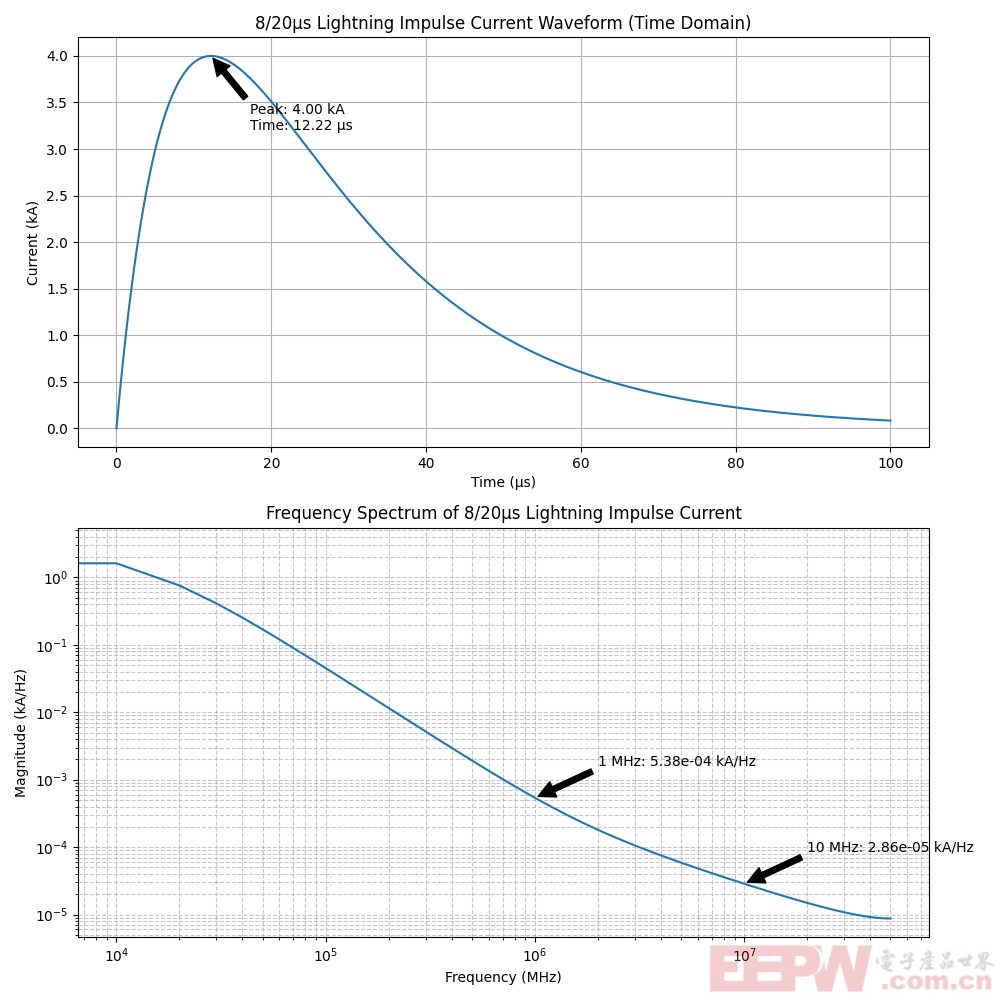
生成的时域波形，展示了8/20μs浪涌波形的典型特性。

3.频域分析

3.1时域到频域的转换

为了分析8/20μs浪涌波形的频率成分，需要将其从时域转换到频域。这一过程可以通过快速傅里叶变换（FFT）实现。FFT的基本原理是将时域信号分解为不同频率成分的叠加，从而得到信号的频谱。

在代码中，`analyze_frequency_domain`函数使用`scipy.fft.fft`计算信号的频域表示。具体步骤如下：

1.计算信号的FFT，得到复数频谱。

2.提取频率数组`freq`和幅度谱`magnitude`。

3.对幅度谱进行归一化处理，使其单位为“kA/Hz”。

3.2频域波形的特性

8/20μs浪涌波形的频域特性可以通过其频谱图进行分析。由于该波形是一个瞬态脉冲，其频谱通常呈现宽带特性，包含从低频到高频的成分。

在代码中，频域波形以对数-对数（log-log）尺度绘制。频谱图展示了信号在不同频率下的幅度分布。通过频谱图可以观察到：

-信号在低频段（如1MHz以下）具有较高的幅度。

-随着频率的增加，幅度逐渐减小，但仍然包含高频成分。

3.3频域分析的意义

频域分析对于理解8/20μs浪涌波形的特性具有重要意义：

1.频谱特性：频域分析可以揭示信号在不同频率下的能量分布，有助于设计滤波器或保护电路。

2.电磁兼容性：通过频域分析，可以评估信号对其他设备的干扰特性，从而优化电磁兼容性设计。

3.实际应用：频域特性可以用于验证设备在不同频率下的抗干扰能力。

4.仿真思路总结

4.1仿真流程

1.时域波形生成：

-使用双指数函数生成8/20μs浪涌波形。

-确保波形的峰值电流为4kA。

2.频域分析：

-使用FFT将时域信号转换为频域信号。

-计算频率数组和幅度谱。

3.结果可视化：

-绘制时域波形图，展示8/20μs浪涌波形的时域特性。

-绘制频域波形图，展示信号的频谱特性。

4.2仿真结果分析

通过仿真可以得到以下结论：

-8/20μs浪涌波形在时域上表现为一个快速上升、缓慢下降的脉冲。

-在频域上，该波形呈现宽带特性，包含从低频到高频的成分。

-频域分析可以为电磁兼容性设计和滤波器设计提供重要参考。

5.结论

通过对8/20μs浪涌波形的时域和频域分析，可以全面理解其特性及其对电子设备的影响。时域分析揭示了波形的瞬态特性，而频域分析则揭示了其频率成分。这种分析方法对于设计抗干扰电路和优化电磁兼容性具有重要意义。

通过本文的仿真思路和代码实现，进一步探索8/20μs浪涌波形的特性，并将其应用于实际工程中。希望这篇文章能帮助大家更好地理解8/20μs浪涌波形的时域转频域分析，同时也希望大家在学习过程中能够保持好奇心和探索精神，不断进步！

附代码：

1. import numpy as np
import matplotlib.pyplot as plt
from scipy.fft import fft, fftfreq
#import B-tron EMC

# Set font to support English display
plt.rcParams["font.family"] = ["DejaVu Sans", "Arial", "sans-serif"]
plt.rcParams["axes.unicode_minus"] = False  # Ensure minus sign display


def generate_8_20_waveform(duration=100e-6, samples=10000):
    """
    Generate 8/20μs standard lightning impulse current waveform

    Parameters:
        duration: Simulation duration (seconds)
        samples: Number of sampling points

    Returns:
        time: Time array (seconds)
        current: Current array (kA)
    """
    t = np.linspace(0, duration, samples)

    # 8/20μs waveform parameters
    tau1 = 8e-6  # Front time constant
    tau2 = 20e-6  # Tail time constant
    amplitude = 4  # Amplitude (kA)

    # Calculate current waveform (exponential decay model)
    current = amplitude * (np.exp(-t / tau2) - np.exp(-t / tau1))

    # Normalize to make peak value 4kA
    current = current / np.max(current) * amplitude

    return t, current


def analyze_frequency_domain(time, signal, sampling_freq):
    """
    Perform frequency domain analysis

    Parameters:
        time: Time array (seconds)
        signal: Signal array
        sampling_freq: Sampling frequency (Hz)

    Returns:
        freq: Frequency array (Hz)
        magnitude: Amplitude spectrum
    """
    n = len(signal)
    yf = fft(signal)
    freq = fftfreq(n, 1 / sampling_freq)[:n // 2]
    magnitude = 2.0 / n * np.abs(yf[:n // 2])

    return freq, magnitude


def plot_waveforms(time, current, freq, magnitude):
    """Plot time-domain and frequency-domain waveforms"""
    fig, (ax1, ax2) = plt.subplots(2, 1, figsize=(10, 10))

    # Time-domain waveform
    ax1.plot(time * 1e6, current)  # Convert time to μs
    ax1.set_title('8/20μs Lightning Impulse Current Waveform (Time Domain)')
    ax1.set_xlabel('Time (μs)')
    ax1.set_ylabel('Current (kA)')
    ax1.grid(True)

    # Mark peak value and time parameters
    peak_idx = np.argmax(current)
    t_peak = time[peak_idx] * 1e6
    ax1.annotate(f'Peak: {current[peak_idx]:.2f} kA\nTime: {t_peak:.2f} μs',
                 xy=(t_peak, current[peak_idx]),
                 xytext=(t_peak + 5, current[peak_idx] * 0.8),
                 arrowprops=dict(facecolor='black', shrink=0.05))

    # Frequency-domain waveform (log-log scale)
    ax2.loglog(freq, magnitude)
    ax2.set_title('Frequency Spectrum of 8/20μs Lightning Impulse Current')
    ax2.set_xlabel('Frequency (MHz)')
    ax2.set_ylabel('Magnitude (kA/Hz)')
    ax2.grid(True, which='both', linestyle='--', alpha=0.7)

    # Add spectral feature annotations
    freq_1MHz = np.interp(1e6, freq, magnitude)
    freq_10MHz = np.interp(1e7, freq, magnitude)



    ax2.annotate(f'1 MHz: {freq_1MHz:.2e} kA/Hz',
                 xy=(1e6, freq_1MHz),
                 xytext=(1e6 * 2, freq_1MHz * 3),
                 arrowprops=dict(facecolor='black', shrink=0.05))

    ax2.annotate(f'10 MHz: {freq_10MHz:.2e} kA/Hz',
                 xy=(1e7, freq_10MHz),
                 xytext=(1e7 * 2, freq_10MHz * 3),
                 arrowprops=dict(facecolor='black', shrink=0.05))

    plt.tight_layout()
    return fig


def main():
    # Generate 8/20μs waveform
    time, current = generate_8_20_waveform(duration=100e-6, samples=10000)

    # Calculate sampling frequency
    sampling_freq = len(time) / (time[-1] - time[0])

    # Frequency domain analysis
    freq, magnitude = analyze_frequency_domain(time, current, sampling_freq)

    # Plot waveforms
    fig = plot_waveforms(time, current, freq, magnitude)

    # Display waveforms
    plt.show()

    # Print magnitude at key frequencies
    print("8/20μs Waveform Frequency Characteristics:__B-tron")


if __name__ == "__main__":
    main()