使用自变分原理改进正则化核回归：通过变分法推导和推广Nadaraya-Watson估计

来源：Deephub Imba

核回归技术是一组非参数方法，用于通过一组数据点拟合平滑的曲线。Nadaraya-Watson 估计就是这样一种方法。它通常是在自变量分布的核密度估计以及因变量和自变量联合分布的基础上，通过计算因变量的条件期望得到的。

在本文中，我将介绍推导 Nadaraya-Watson 估计（本篇文章中将其简称为“核回归”）的另一种基本原理。这个基本原理激发了一个变分原理，这将使我们能够制定一个可以称为“正则化核回归”的修改。

许多回归技术可以通过最小化关于二次损失函数的经验风险或关于 N 个数据点 (x₁, y₁) 的残差平方和 R[f] 推导出来，...：

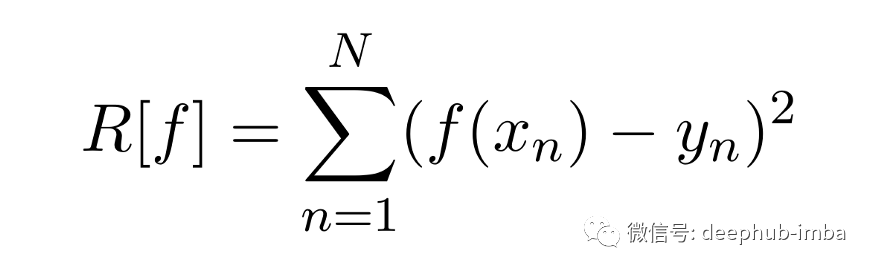
相对于未知回归函数 f 最小化问题，该表达式是不适定的，所以需要对 f 进行进一步的假设。在参数化建模中，我们将 f 限制在某个假设空间中以使问题成为适定的。例如，在线性回归中，我们将 f 限制在仿射线性函数的空间，f(x) = m⋅ x + c。确定斜率 m 和截距 c 使得上述残差平方和最小，将产生最佳拟合曲线。现在让我们对上述公式应用一些数学变换，并逐步解释这些：

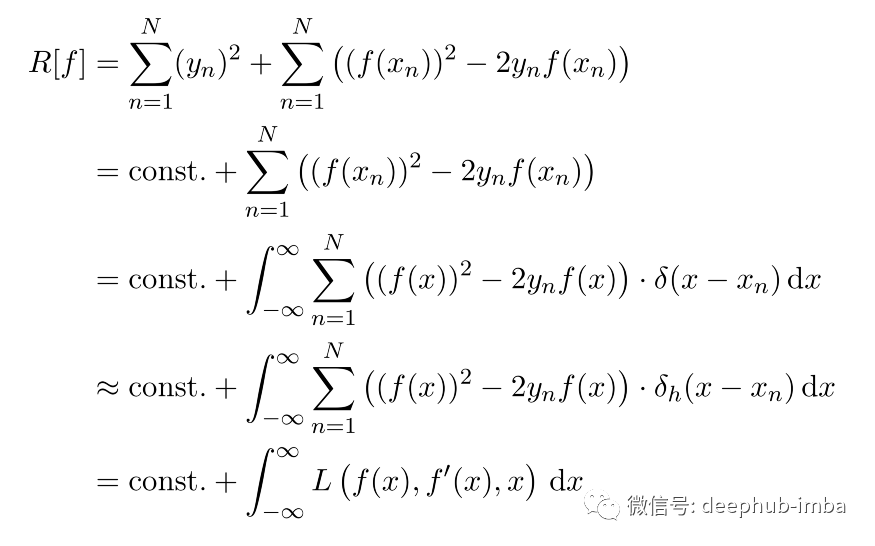
第一个等式就是把平方展开，把y的平方展开作为它们自己的和。对于第二个等式，y的平方和对我们以后要应用的最小化过程没有帮助因为它不依赖于我们想要最小化的函数f。因此，我们可以称它为“const”。我们就不用管它了。

下一步至关重要。我们可以通过狄拉克δ函数来计算f在一个固定位置的值，就像这样:

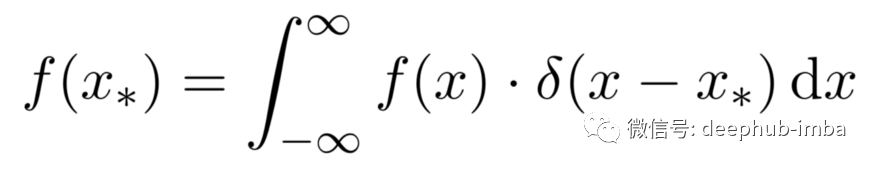
这将允许我们将整体损失 R[f] 写成一个积分，并且经验风险最小化变得可以通过变分计算的标准工具进行。

δ（delta）的正确定义需要对泛函分析有一定的了解，更准确地说是分布理论或“广义函数”的理解。但是根据我们的最终目标，可以将狄拉克δ函数想象为以原点为中心的非常窄的峰。我们可以通过新生 delta 函数的极限来近似狄拉克 δ 函数（新生成函数的度量在原点附近变得越来越集中）。

一般情况下这个名字就出现了 - 高斯：

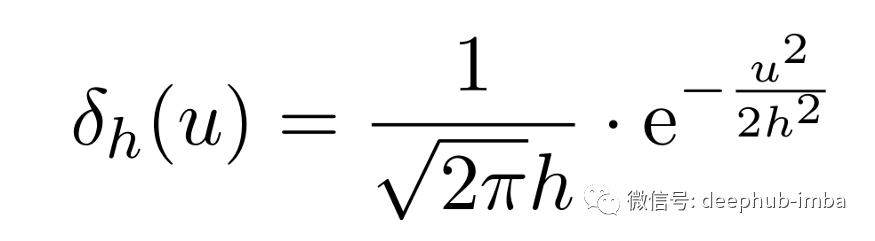
这个函数族消失在 > 0的极限下，并在适当的意义上收敛于狄拉克函数。

最后，在用上述近似代替狄拉克函数之后，我们可以给出积分下的公式的名称:L代表拉格朗日。(这个特定的拉格朗日函数实际上并不依赖于f '的导数，但我们稍后会用到它的通用性)

找到像这样一个函数的平稳点——即一个用拉格朗日函数的积分表示的点——在数学和理论物理中有许多应用。例如，经典力学可以被重新表述为基于最小作用量原理的拉格朗日力学。另一个应用是对光线路径的描述，它遵循费马原理，也就是最小时间原理。

因此，这个问题有一个众所周知的通解。但在这里我们感兴趣的是最小化以下形式的函数:

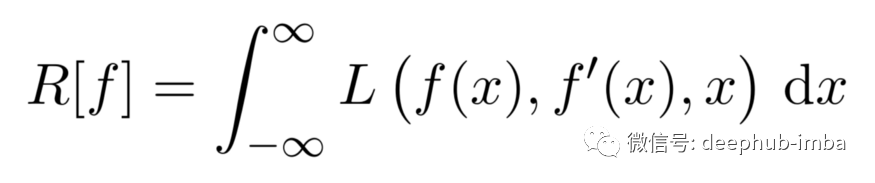
函数f是当且仅当满足以下欧拉-拉格朗日方程时的平稳点:

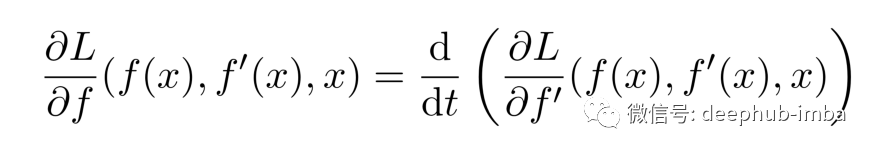
对于我们到目前为止导出的拉格朗日函数，通过最小二乘法 R[f] 的“抹去”和，所以右侧消失了，因为导数 f ' 没有依赖关系。

在这种情况下，欧拉-拉格朗日方程可以简单地用代数方法求解f(x):

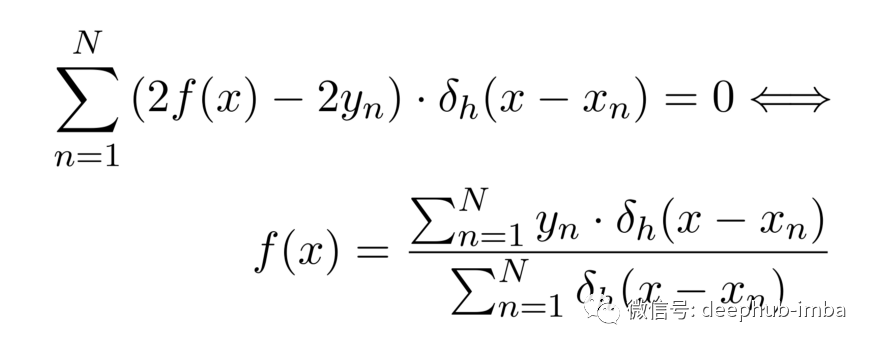
这正是 Nadaraya 和 Watson 提出的核回归公式。

到目前为止，我们能够推导出经过验证的回归技术。现在可以进行更多的研究了，我们对变分原理进行一些修改。例如，可以添加一个使模型正则化的项，并惩罚大导数：

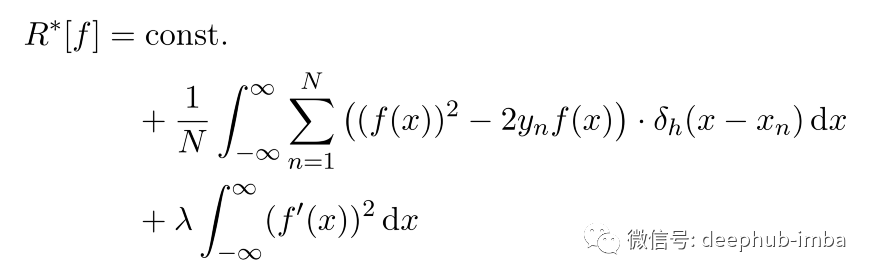
λ > 0是一个正则化参数。我们还引入了常数因子“1 / N”，因此我们实际上是将平均经验风险与正则化项进行比较。计算相应的欧拉-拉格朗日方程是一项简单的任务:

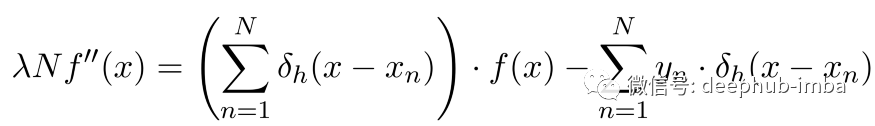
当然，对于λ = 0，这个公式可以简化为传统的核回归。这是一个二阶线性微分方程一旦给出边界条件或初始条件它就有唯一解。在R中，solve和bvpSolve包可以用于数值求解常微分方程。

让我们模拟一些真实的数据。下图显示了Berkeley Earth (http://berkeleyearth.org/data/):)的1850年至2019年全球平均气温的时间序列

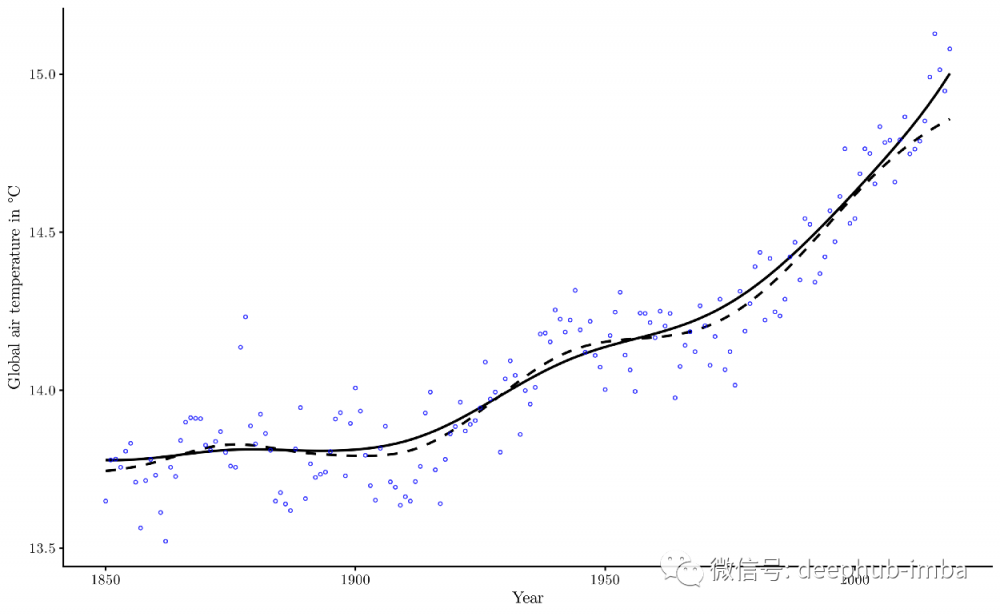
虚线是bandwidth  h = 10.0的常规核回归，实线是相同bandwidth 和正则化参数λ = 0.5的正则化核回归的结果。欧拉-拉格朗日方程是通过施加一个边界值问题来求解的，该边界值是由前五年/最近五年的温度中值给出的最早/最近的温度。

本文提出的正则化核回归有一些明显的缺陷，例如:

边界条件需要被指定，这看起来像是一个特别的过程，

尝试应用初始条件似乎并不实际，而且会导致荒谬解决方案，

在λ很小的情况下，数值可能不稳定。

但是该模型似乎也有一些理想的功能。例如，对于不同的bandwidth 选择，它似乎相当健壮。下图显示了h = 1.0时使用相同的数据和回归的函数，但bandwidth 更小:

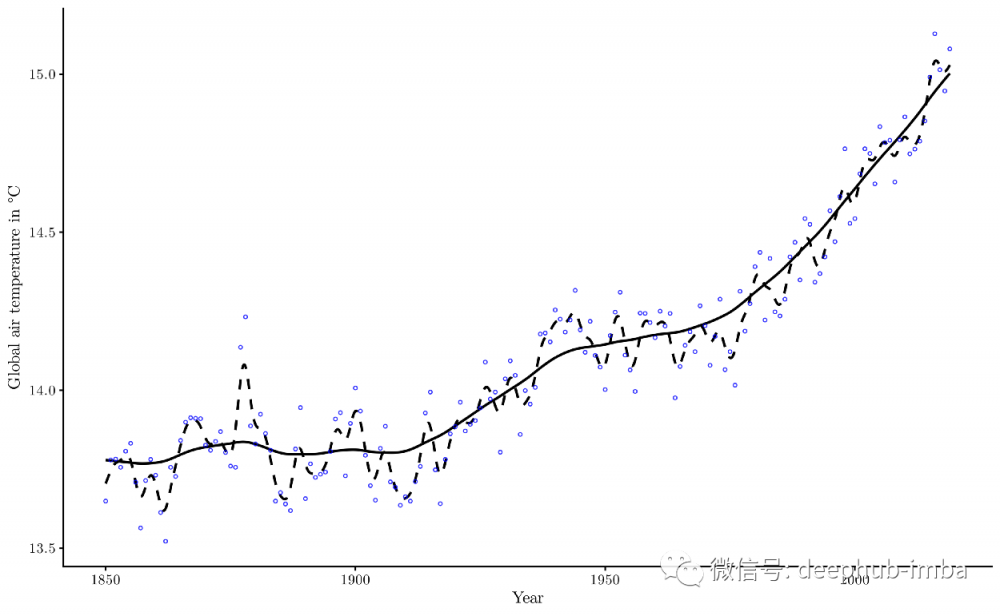
传统的核回归似乎在很大程度上过度拟合了数据，但正则化版本“保持在正确的轨道上”。

该模型的另一个特点是:它可能更擅长处理丢失的数据。这里有一个图表，说明了同样的回归技术，但缺失1920年和1970年之间的数据:

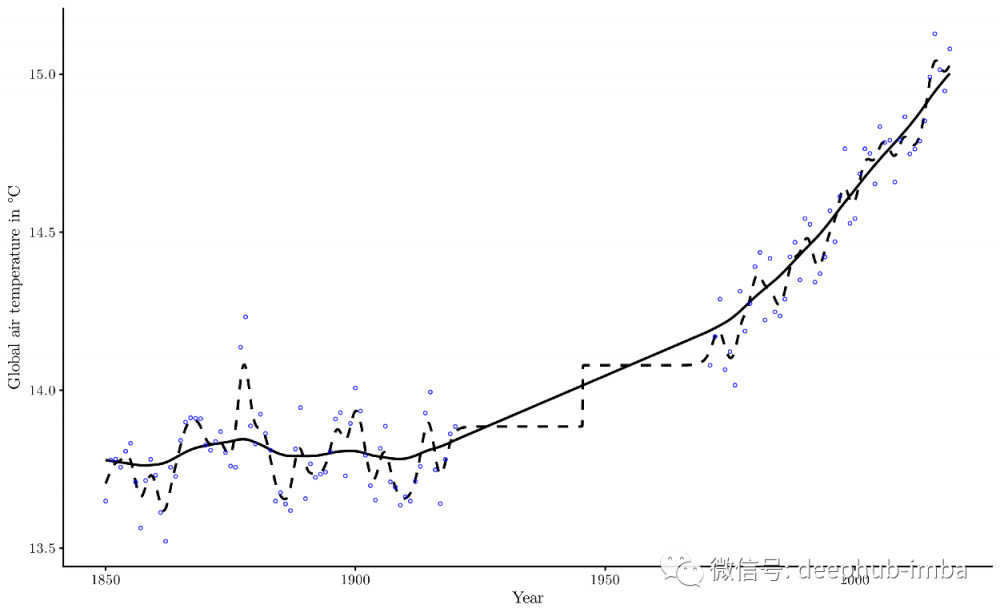
我们可以利用这种健壮性来处理丢失的数据，并尝试推断出未来场景的时间序列。虽然传统的核回归在插值中肯定是有用的，但我们可以预期传统的技术在这项任务中会失败。

然而，正则化的核回归可能会成功，因为增加了“惯性”λ。以下图表显示了对未来情景的先验预测，即2040年全球平均气温将分别上升到15.2摄氏度、15.8摄氏度和16.4摄氏度:

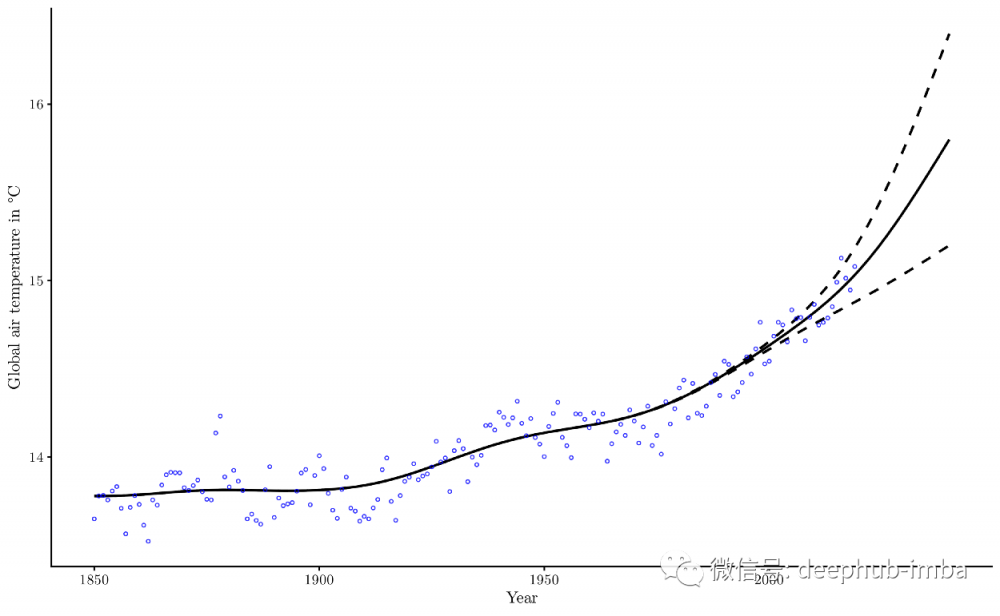
对于每个外推，使用相同的模型超参数h = 10.0， λ = 0.5。尽管在拟合最终模型之前给出了先验，但 2040 年 15.8 °C 的选择并不是临时的：推算到 2040 年的 15.8 °C 实际上是最好的预测，因为有了这个参数，（传统的） 残差平方和被最小化，这可以通过简单的网格搜索来验证。

核回归是一种技术，可以通过最小化与二次损失函数相关的经验风险的“平滑”或“涂抹”推导出来。这种方法导致可以扩展的变分原理，例如通过添加正则化项。

对结果模型的一些实验显示了一些理想的特性，它可能会在预测时间序列中找到有用的应用。