惯性变化时无刷直流电机的鲁棒控制器设计

1 引言

随着电力电子技术和先进电机控制理论的发展，无刷直流电机（bldcm）得到了广泛应用。确定无刷直流电机调速性能优劣的重要指标就是快速性、稳定性和鲁棒性。传统的无刷直流电机调速系统一般采用双闭环控制，内环为电流环，外环为速度环，控制策略一般采用pi/pid控制。随着控制技术的迅猛发展，现在已有很多先进控制策略被应用于无刷直流电机的调速中[1][2][3]。

鲁棒控制器对系统参数变化不敏感，因此它能保证系统的稳定性和好的动态性能。鲁棒控制器采用q参数化理论，可以有以下几个方面的优点：稳定的控制器总是存在、闭环极点能配置在左半平面的指定区域以保证所需要的动态响应、所有稳定的控制器都可以由一个独立的参数q来描述。该理论已成功地应用于诸多控制等领域[4][5][6][7][8]。本文采用q参数化理论，设计了无刷直流电机的鲁棒控制器。仿真结果表明：当参考速度、负载转矩和电机惯性参数发生变化时，本文提出的控制器都具有响应速度快、跟踪误差小、干扰抑制能力强、调速效果好等特点。

2 无刷直流电机模型

以一台三相桥式y接无刷直流电机为例，假设：忽略齿槽效应，绕组均匀分布；忽略磁路饱和，不计涡流和磁滞损耗；不考虑电枢反应，电机反电势为梯形波。则电机的状态方程为[9]：

(1)

其中：p为微分算子，l 为绕组自感，m为绕组互感，ia，ib，ic分别为三相相电流，va，vb，vc为三相相电压，ea，eb，ec为三相反电势。

电磁转矩方程为

te=(eaia+ebib+ecic)/ωr (2)

运动方程为

pωr =( te – tl-bωr)/j (3)

式中ωr为电机的角速度；b为阻尼系数；j为转动惯量；tl为负载转矩。

在s-域重写方程(3)为

ωr=gp(s)( te(s)-tl(s)) (4)

式中
(5)

根据以上分析，基于鲁棒控制的无刷直流电机控制系统框图如图1所示。

图中的速度控制器k(s)利用q-参数化理论来设计，以消除一些传统的控制器不容易解决或解决效果不好的问题。

3 控制器设计

3.1 单参数控制器设计

q-参数化理论[10]指出：对于一个给定的单输入、单输出机械系统（包含驱动系统），其所有的稳定控制器均可用一个独立参数q来描述。图1中的控制器即为一个单参数控制器，用来控制由式（5）所描述的系统。图1中，u1=ωr*为参考输入信号，u2= n是传感器噪声，u3=tl为负载转矩，is*为控制器的输出，ωr为待调节的系统输出，k(s)为一个稳定的控制器。为了描述gp(s)的所有稳定的控制器k ，我们首先建立gp(s)的一个双互质分解，如下述公式所示。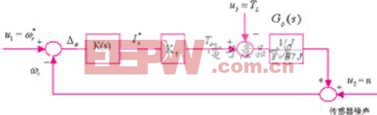



图1 无刷直流电机驱动的控制系统框图


(6)
(7)
(8)

考虑由方程（5）所描述的被控对象，这里gp(s)。将ktgp(s)用状态空间形式描述，则有：

(9)

式中ag,bg,cg的值由下述方程决定：
ag=-b/j
bg=1
cg=kt/j

根据上述分析结果，可以得到的计算式如下：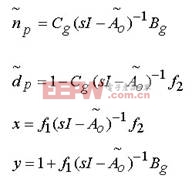



这里f1和f2的选择必须使得和是hurwitz的。

综上所述，控制器传递函数用ktgp(s)和q描述则为：
(10)
3.2 控制器的设计约束

以ωr作为输出，u1，u2，u3作为输入，则可得相应的闭环传递函数分别为：
(11)
(12)
(13)
本文所设计的控制器必须满足以下一些设计约束：

(1)跟踪性能：输出速度(ωr)必须能够跟踪其参考输入(ωr*)，即满足：



要满足上式，则需选择q使得的直流增益为1，即。