如何选择电容器实现高性能的EMI滤波
电气器噪声可以以许多不同的方式引起。在数字电路中,这些噪声主要由开关式集成电路,电源和调整器所产生,而在射频电路中则主要由振荡器以及放大电路产生。无论是电源和地平面上,还是信号线自身上的这些干扰都将会对系统的工作形成影响,另外还会产生辐射。
本文将重点讨论多层陶瓷电容器,包括表面贴装和引脚两种类型。讨论如何计算这些简单器件的阻抗和插入损耗之间的相互关系。文中还介绍了一些改进型规格的测试,如引线电感和低频电感,另外,还给出了等效电路模型。这些模型都是根据测得的数据导出的,还介绍了相关的测试技术。针对不同的制造工艺,测试了这些寄生参数,并绘制出了相应的阻抗曲线。
阻抗和插入损耗
所幸的是,电容器还算简单的器件。由于电容器是一个双端口器件,故仅有一种方法与传输线并接。不要将该器件看作一只电容器,更容易的方法是将其看作为一个阻抗模块。当其与传输线并联时,甚至可以将其视作为一个导纳模块(见图1)。
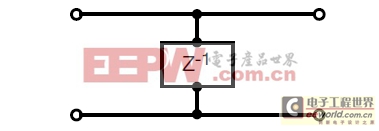 |
图1:将电容器视作为阻抗模块。 |
 |
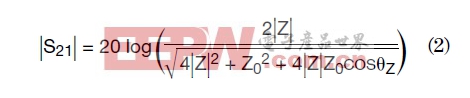 |
Z0=传输线阻抗
??=阻抗模块的相角
有一些插入点可以来观察方程2。首先,对于一个高性能的陶瓷电容器来说,其相角在整个频段中都非常接近±90°,只有谐振点附近除外(见图2)。
 |
图2:1000-pF陶瓷电容器的典型阻抗幅相特性。 |
已知±90°的余弦接近0,故方程2可以被简化为:
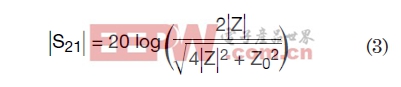 |
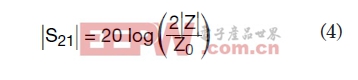 |
 |
表1:1000-pF旁路电容器的阻抗和求得的插入损耗。 |
这些方程中的唯一问题就是需要知道一系列不同电容值的阻抗。
多层陶瓷电容器(MLCC)串联模型
对于MLCC电容器来说,最简单的(当然也是最有效的)模型是串联模型(见图3)。
 |
图3:陶瓷电容器的等效串联模型。 |
该模型给出了适用于绝大多数表面贴装MLCC的正确阻抗曲线。记住电容值将随温度和直流偏置而变化。等效串联电阻(ESR)随温度、直流偏置和频率变化,而等效串联电感(ESL)却基本保持不变。对阻抗来说,也许最重要的部分是谐振点,因为这是衰减最大的频率。众所周知,计算谐振频率的公式是:
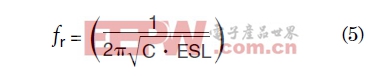 |
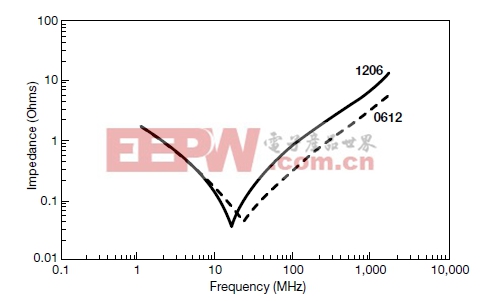 |
图4:两只0.1 μF电容器的阻抗曲线比较。 |
低电感电容的最大优点体现在数字电路退耦中。利用如下简单的电感方程:
 |
引脚电容器
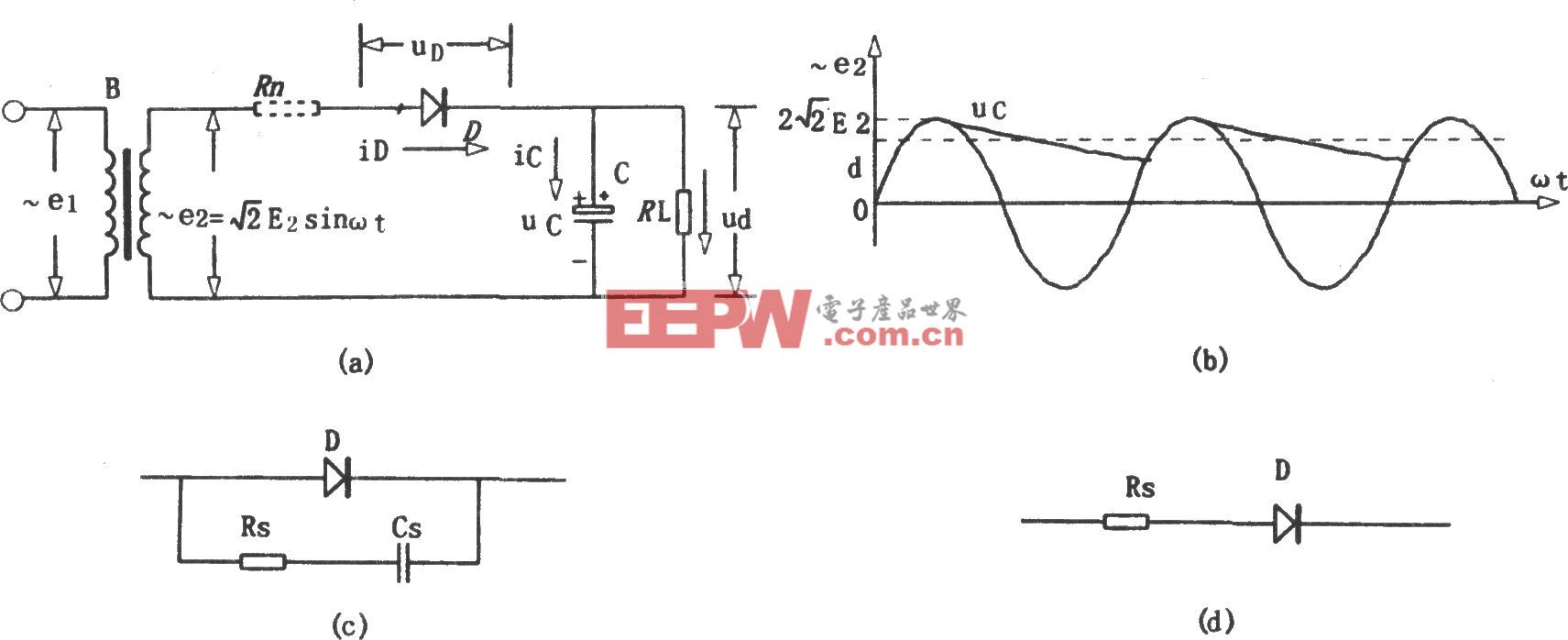
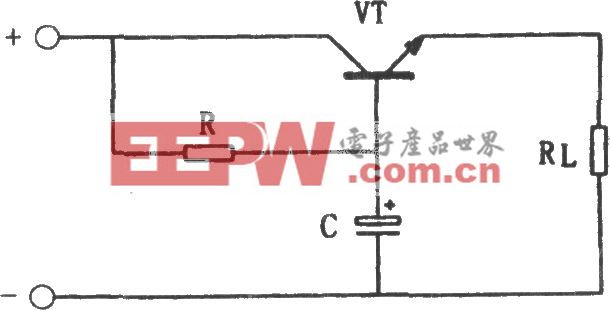
引脚电容相对于表面贴装电容器,除了增加了引脚之外,其他并没有什么不同。其等效模型与MLCC模型一样,除了增加了引脚所产生的电感之外,见图5。




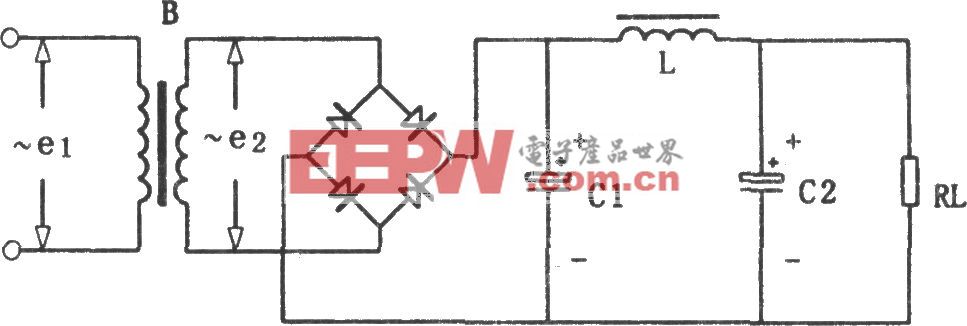




评论