用史密斯圆图学习短截线调谐

使用史密斯圆图了解阻抗匹配短截线调谐，以及单和双短截线调谐、阻抗轮廓和史密斯圆图的“禁区”。

在本文中，您将看到使用史密斯圆图将RF传输线与各种负载相匹配的短截线调谐示例的概述。如果你发现自己在射频领域工作，那么使用史密斯圆图设计这些匹配电路的能力会很方便，因为它通常比计算分析方程更直观、更快。史密斯圆图是电气工程师菲利普·哈格·史密斯的发明。在另一篇文章中，我们讨论了如何使用分流短截线来提供阻抗匹配。此外，阻抗匹配也可以通过串联短截线来实现，我们稍后会讨论。然而，如果负载阻抗有一些变化，则不能使用单短截线匹配。在这些情况下，更好的选择是使用双存根匹配网络，这是本文的重点。

单短截线调谐——并联和串联配置

在射频工程中，将线路与其负载相匹配至关重要。阻抗匹配可以使用各种不同的方法和组件来实现，每种方法和组件都适合特定的应用。当然，这导致了一个不可避免的、留存已久的困境，即工程师必须在最好的解决方案和最便宜的实施之间取得平衡。

短截线调谐是满足这两个标准的一种方法。一般来说，短截线调谐只是将传输线的长度添加到串联或并联电路配置中的现有长度上，以使线路与负载相匹配的过程。这是通过将特定长度的短截线放置在距离负载特定距离处来实现的。图1显示了短截线调谐器的两种基本布局，即分流短截线（图1（a））和串联短截线（表1（b））匹配网络。

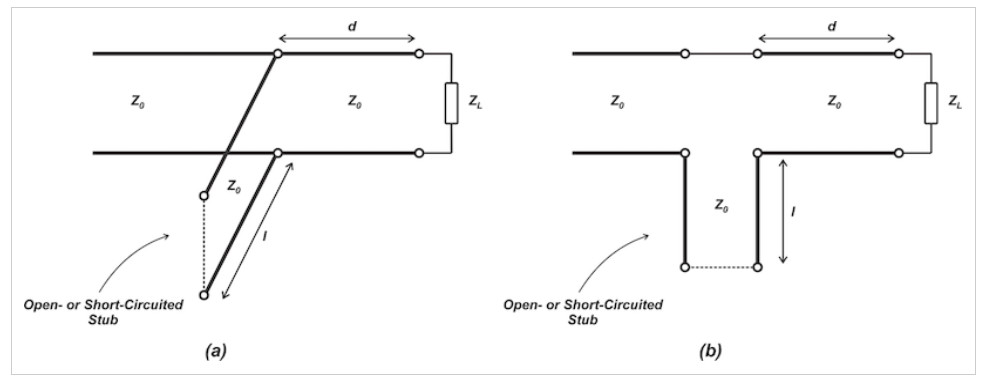
图1分流短截线（a）和串联短截线（b）匹配网络的示意图

分流短截线法（将在另一篇文章中更详细地讨论）更受欢迎。这是因为分流配置不需要断开现有的连接，因此在机械上更方便。然而，为了完整起见，我们将通过一个示例简要讨论系列配置。

示例1：串联单桩匹配网络

设计图1（b）的串联单短截线匹配网络，将ZL=100+j50Ω转换为ZIn=50Ω。假设存根在短时间内终止。如果负载阻抗是串联RL电路，匹配频率为1 GHz，则绘制反射系数幅度与频率的关系图。

归一化负载阻抗zL=2+j标记在图2中的史密斯圆图上。

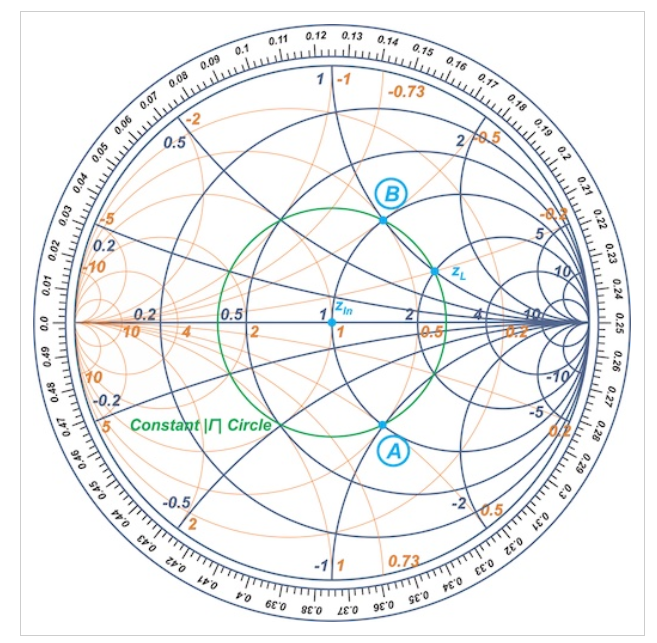
图2史密斯圆图上的归一化负载阻抗zL=2+j

图1（b）中的匹配电路从负载侧的一条长度为d的串联线开始。我们知道，离开传输线上的终端会沿着负载的常数|Γ|圆产生顺时针旋转。因此，在串联线输入端看到的阻抗轨迹是负载常数|Γ|圆——上图中的绿色圆。

添加短截线只会改变阻抗的电抗分量。因此，应选择长度d，将我们移动到r=1的恒定电阻圆。接下来，短截线电抗可以使我们沿着r=1的圆到达史密斯圆图的中心。上图中有两个交点，分别表示为点A和B。使用点A，我们得到如图3所示的路径。

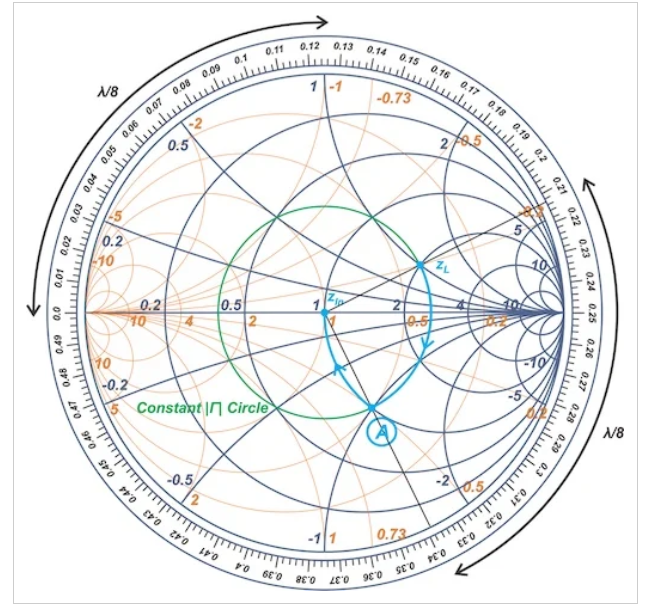
图3史密斯圆图上A点的路径

为了找到级数线的长度d，我们可以从中心通过zL和点A向外画线到图表的边缘，并测量相应的弧，得出d=λ/8。为了找到短截线的长度，我们应该考虑点A的阻抗。点A的归一化阻抗为1-j。因此，短截线应该提供+j的电抗，以将我们移动到史密斯圆图的中心。对于短路短截线，短截线的长度为λ/8，如上所示。最终的匹配电路如图4所示。

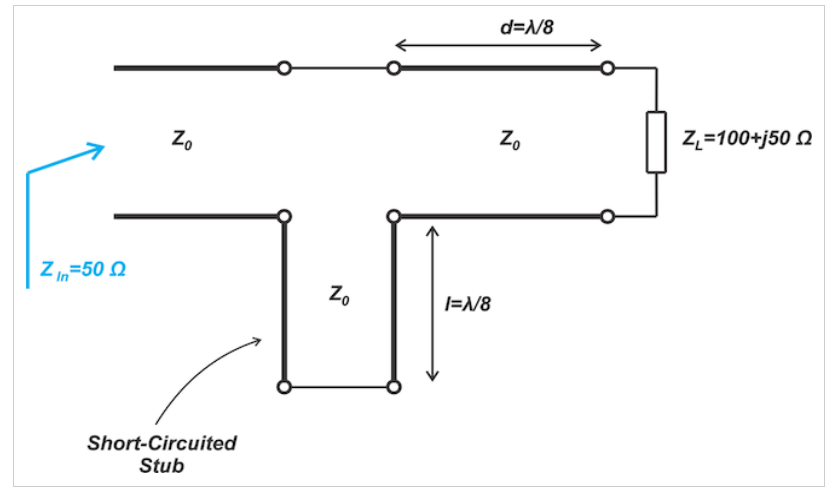
图4我们第一个例子的最终匹配电路图

由于ZL=100+j50Ω被称为串联RL电路，匹配频率为1 GHz，因此我们得到R=100Ω和L=7.96 nH。如下图5所示，电路的输入反射系数（S11）证实了在1 GHz下的出色匹配。

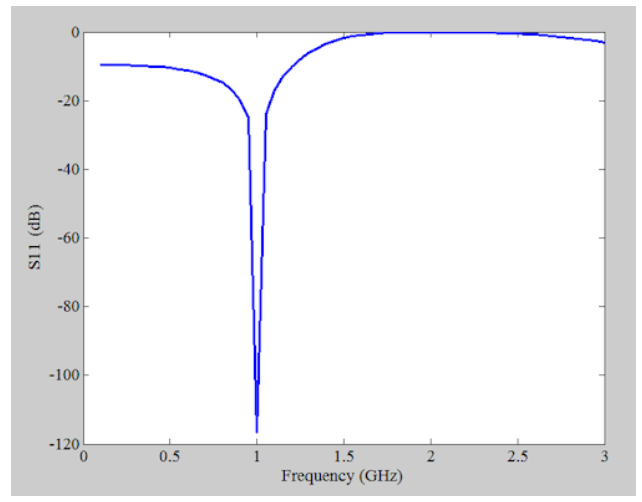
图5显示1 GHz下输入反射系数与频率的图表

现在让我们学习双短截线调谐技术。

双桩匹配网络的基本思想

单个短截线调谐器可以在输入阻抗和负载阻抗的任何值之间提供阻抗匹配，只要它们具有非零实部。这就是为什么单存根调谐非常有效和通用的原因；然而，它有一个缺点，在某些应用中可能会造成问题：短截线的位置和长度都取决于负载阻抗。例如，考虑下面显示的匹配网络（图6）。

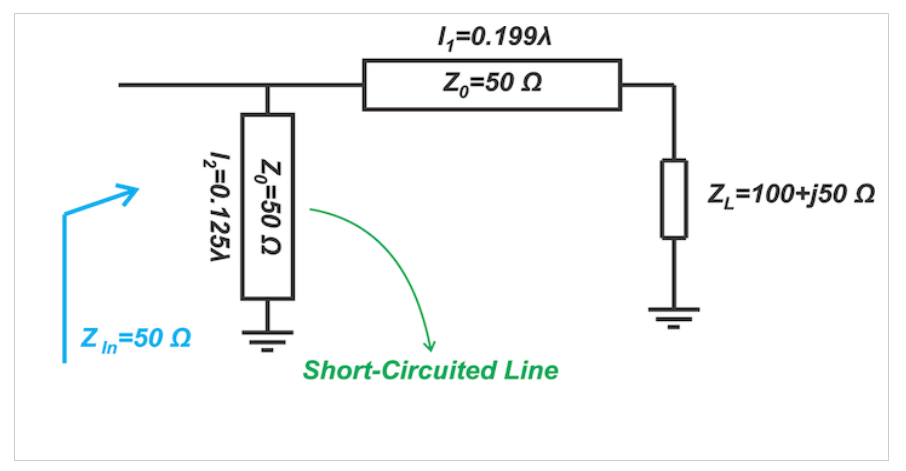
图6匹配网络图示例

短截线与负载的距离为l1=0.199λ。如果负载阻抗不恒定或因制造公差而变化，那么我们必须调整l1和l2。对于将短截线放置在线路负载端的其他类型的分流短截线调谐器也是如此。图7中显示了一个示例。

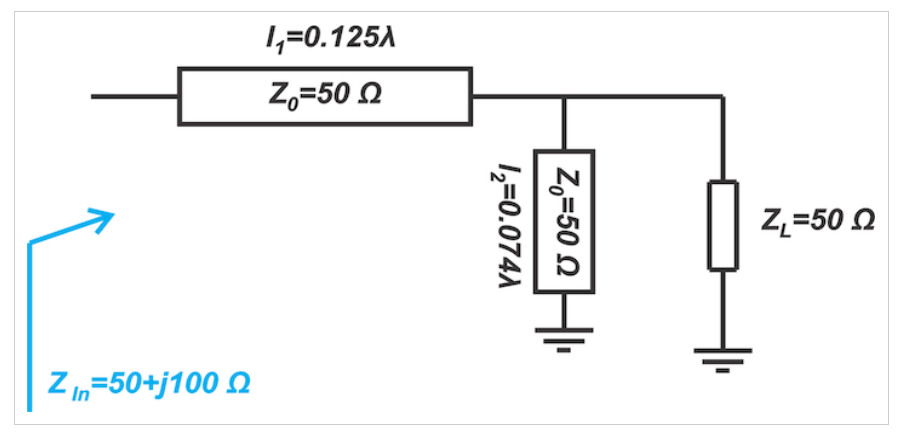
图7 短截线放置在线路负载端的示例图

同样，l1和l2都需要调整，以考虑ZL的变化。调整l1不方便，因为它被放置在负载和输入端口之间。然而，调整短截线l2的长度可以相对容易，特别是在使用短路短截线时。这种可调短截线可以通过沿同轴线移动的滑动短截线来创建。这一观察结果是双短截线调谐器匹配电路的基础，如图8所示。

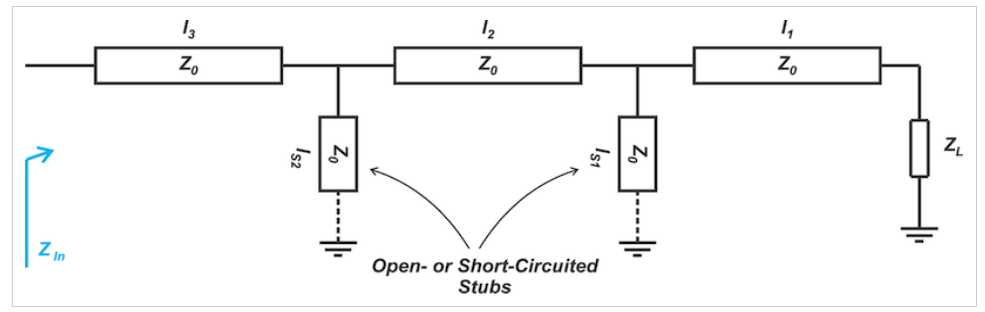
图8匹配电路或双短截线调谐器的示意图

在这种情况下，输入和输出端口之间的串联部分的长度是固定的（l1、l2和l3是恒定的），但短截线长度ls1和ls2是可调的。请注意，通过固定系列线的长度，我们在设计中失去了一个自由度。为了弥补这一点，使用了两个可调短截线，而不是一个短截线。这给了我们两个自由度，类似于单个短截线调谐器的情况。因此，虽然两个短截线的位置是固定的，但它们的长度是可调的。从这里开始，短截线可以在开路或短路时终止。

在解释双短截线调谐器的工作原理之前，研究串联线如何在史密斯圆图上旋转给定的阻抗轮廓是有帮助的。

通过串联线旋转阻抗轮廓

我们知道，离开传输线上的终端会沿着负载的常数|Γ|圆产生顺时针旋转。如果线的电长度为θ，则史密斯圆图上的旋转为2θ（图9）。

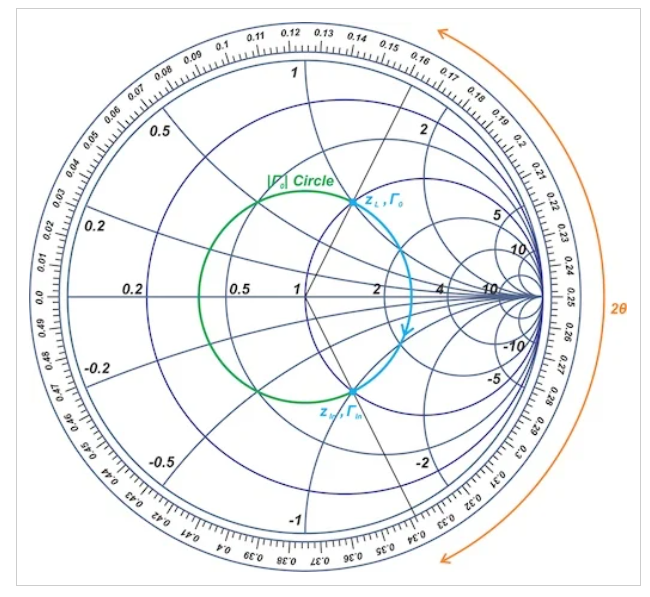
图9旋转2θ的史密斯圆图示例

上述变换不仅可以旋转单个点，还可以明显地旋转史密斯圆图上的给定轮廓。例如，假设负载导纳yL的轨迹是g=1的恒定电导圆（图10中的蓝色圆）。

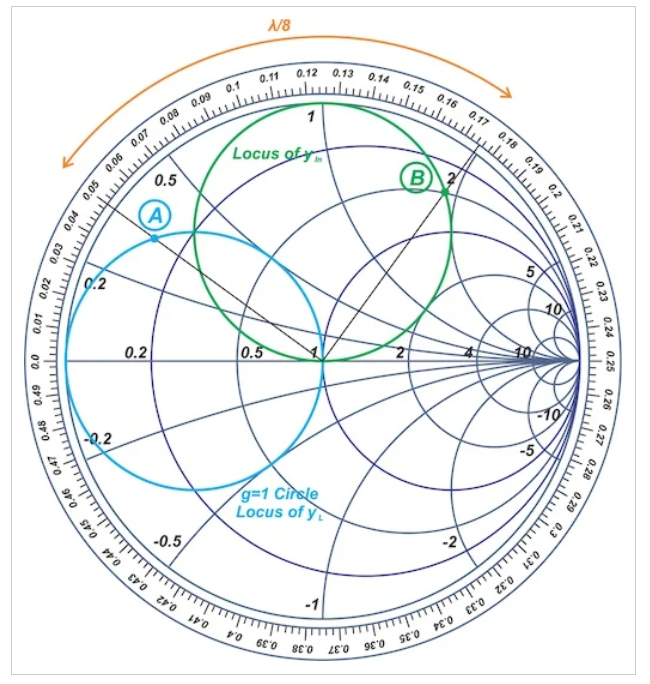
图10史密斯圆图显示了负载导纳yL的轨迹

如果我们在yL中终止一条λ/8的线，则可以通过将g=1的圆顺时针旋转λ/8（或2×45°=90°），得到该线输入处的导纳轨迹，从而得到上图中的绿色圆。

可以看出，蓝色圆圈上的每个任意点都旋转了λ/8，以在绿色圆圈上产生其对应的点（例如，点A被转换为点B）。因此，一条系列线会旋转整个轮廓。

双短截线调谐是如何工作的？

考虑图11所示的双短截线匹配网络。

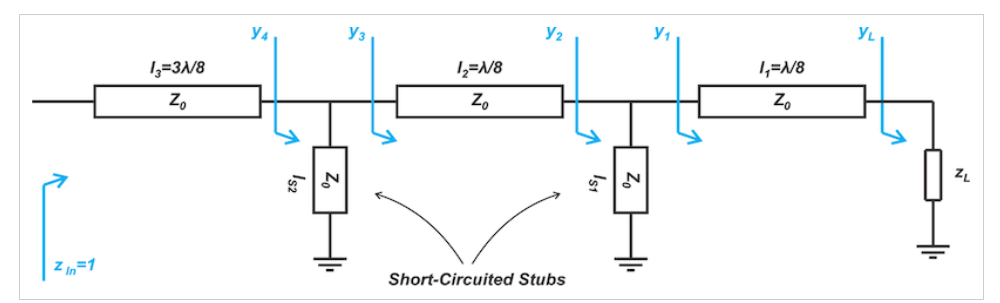
图11双短截线匹配网络示例

在这种情况下，我们有l1=l2=λ/8，l3=3λ/8，短截线在短路中终止。目标是将任意负载阻抗zL转换为zin=1的归一化阻抗。输入端口处的导纳为yin=1。由于尹位于史密斯圆图的中心，y4也位于中心。如果长度为ls2的短截线的电纳为jbs2，则y3=1-jbs2。换句话说，y3位于g=1的恒定电导圆上。

从我们之前的讨论中，我们知道长度为l2的中间串联线将y2顺时针旋转两倍于线的电长度，从而产生y3。因此，我们只需要将y3逆时针旋转λ/8即可找到y2的轨迹。y3和y2的轮廓如图12中的绿色和蓝色圆圈所示。

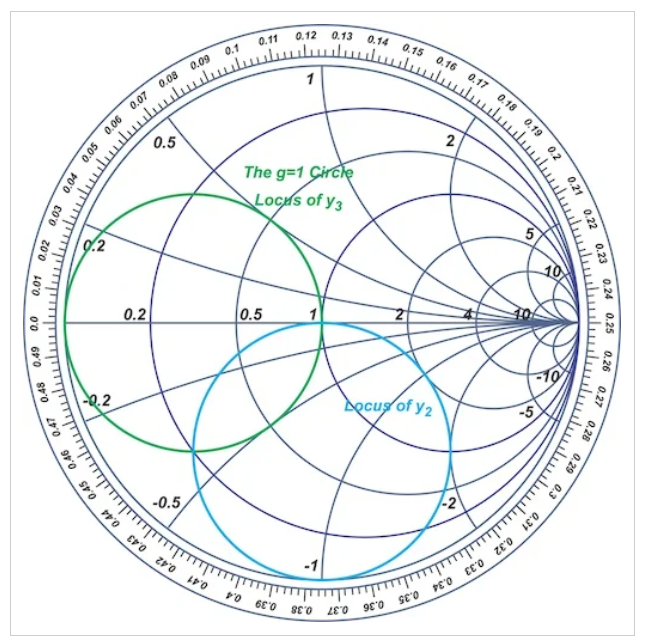
图12史密斯圆图显示y3和y2的轮廓

上述解释表明，如果y2在蓝色圆圈上，y3将在绿色圆圈上，因为l2等于λ/8。在这种情况下，正确选择的短截线长度ls2可以将y4移动到史密斯圆图的中心。因此，我们选择第一个短截线ls1的长度将y2移动到蓝色圆圈上的某个地方，并选择ls1将y4带到史密斯圆图的中心。

请注意，史密斯圆图上蓝色圆圈的位置由中间系列线l2的长度决定。在讨论双短截线调谐时，这个圆通常被称为“旋转1+jb圆”或“旋转g=1圆”。让我们来看一个例子。

示例2：设计双桩匹配网络

设计图11的双短截线匹配网络，将ZL=100+j50Ω转换为ZIn=50Ω。如电路图所示，我们有l1=l2=λ/8和l3=3λ/8，短截线在短路中终止。如果负载阻抗是串联RL电路，匹配频率为1 GHz，则绘制反射系数幅度与频率的关系图。

归一化负载导纳yL（对应于zL=2+j）标记在图13的史密斯圆图上。

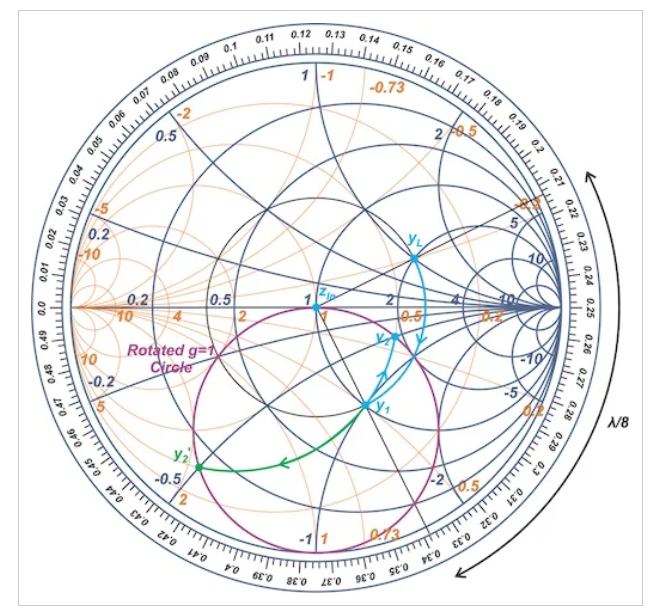
图13史密斯圆图显示了归一化负载导纳yL

如上所述，由于负载侧的串联线，λ/8的顺时针旋转将yL转换为y1。

在这个例子中，y1位于g=0.5的圆上，第一个短截线添加的电纳应该将我们移动到g=0.5圆与旋转的g=1圆（紫色圆）的交点。考虑到这一点，有两种可能的解决方案，分别用y2和y2′表示。在这个例子中，我们将选择使用通过y2的路径。接下来，中间的级数线产生λ/8顺时针旋转，并将我们带到g=1圆上的y3（图14）。

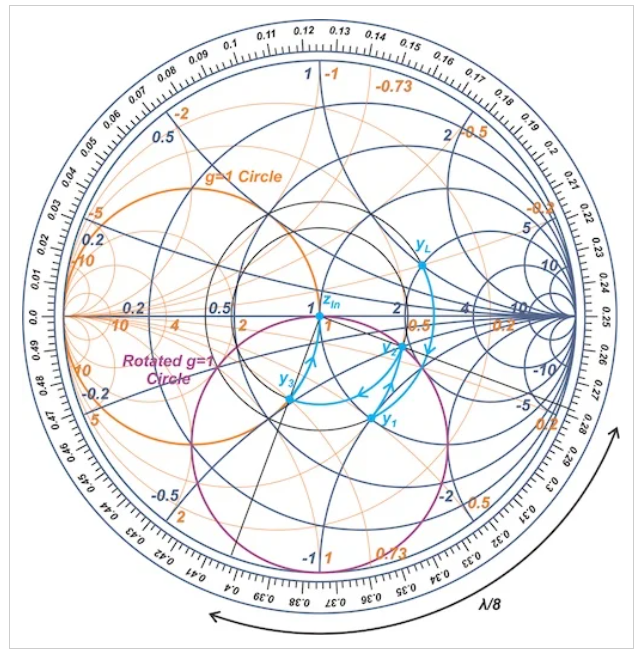
图14史密斯圆图显示了中间的级数线如何产生λ/8顺时针旋转，并将我们带到g=1圆上的y3

最后，第二个存根添加了适当的电纳值jbs2，将我们移动到史密斯圆图的中心。图15显示了具有所需恒定电纳弧的最终路径，因此我们可以计算ls1和ls2。

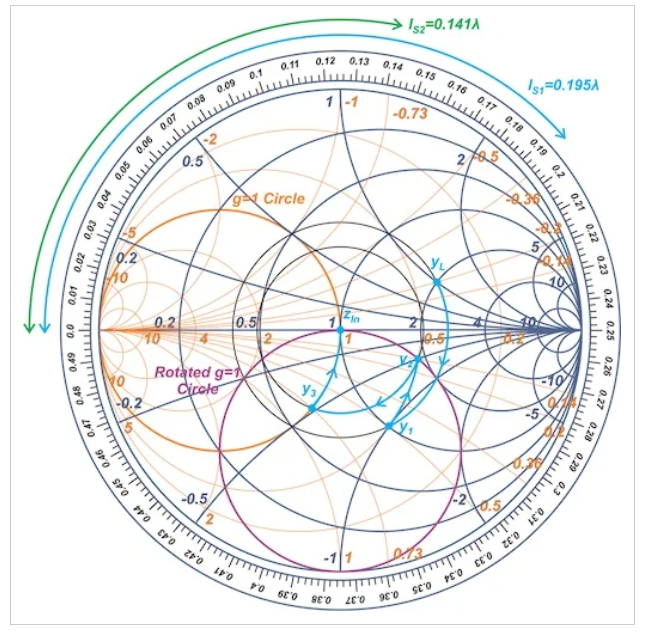
图15史密斯圆图显示了具有所需恒定电纳弧的最终路径

第一个短截线的电纳等于y2和y1之间的电纳差，导致bs1=j0.14-j0.5=-j0.36。如图所示，长度为ls1=0.195λ的短路短截线产生电纳bs1=-j0.36。此外，第二个短截线应产生等于bs2=-j0.73的电纳，以将我们移动到史密斯圆图的中心。这需要一个长度为ls2=0.141λ的短路短截线，如图15所示。这样就完成了设计。

由于ZL=100+j50Ω被称为串联RL电路，匹配频率为1 GHz，因此我们得到R=100Ω和L=7.96 nH。电路的输入反射系数（S11）如图16所示，这证实了在1 GHz下的良好匹配。

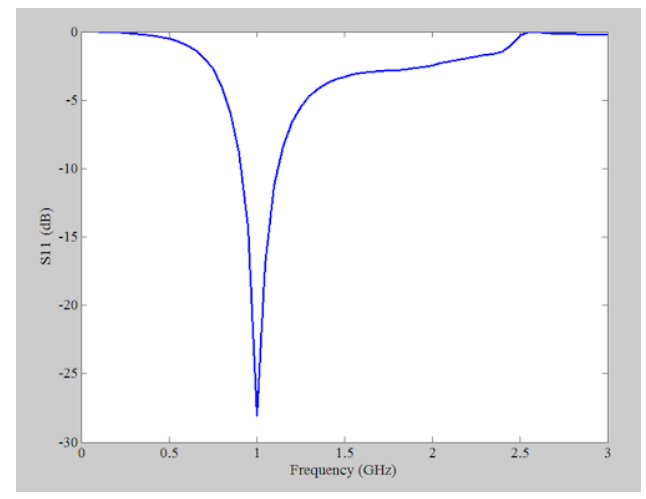
图16显示电路的输入反射系数（S11）在1 GHz下的匹配良好的图表

史密斯图禁区

上述设计过程基于这样的假设，即由第一短截线添加的导纳可以将y2移动到旋转的g=1圆上的一个点。对于yL和l1的某些值，这可能是不可能的。在上述示例中，如果y1落在g=2圆内，则添加电纳不能将其转换为旋转的g=1圆上的点。如图17所示。

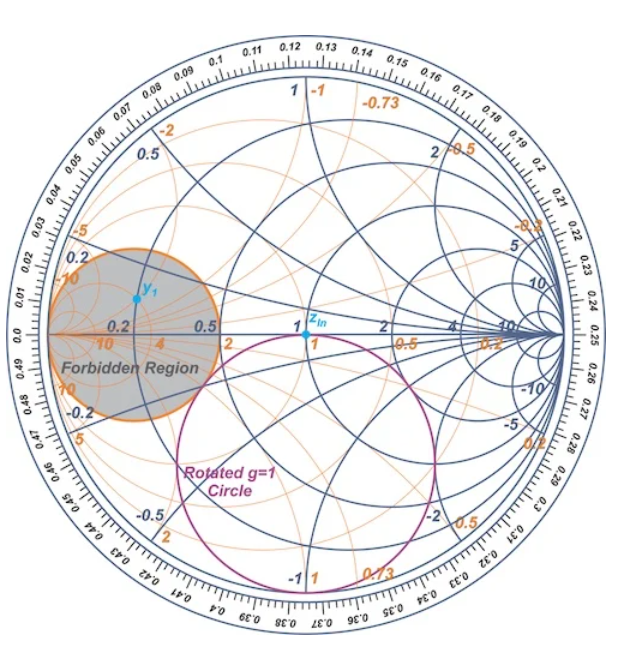
图17史密斯圆图显示了“禁区”

这就是为什么在我们的例子中，g=2圆内的区域是禁区。为了解决这个问题，商用双短截线调谐器选择l1=l3±λ/4，您可以在Reinhold Ludwig和Gene Bogdanov的这本推荐书《RF电路设计：理论与应用》中了解更多信息。在这种情况下，如果负载落在禁止区域内，则可以简单地将负载连接到调谐器的另一端，以将y1移出禁止区域。

通过Z史密斯圆图进行设计

可以仅使用阻抗史密斯圆图（或Z史密斯圆图）而不是使用ZY-Smith图来执行上述计算。在这种情况下，Z史密斯圆图被解释为Y史密斯圆图。你可以在David M.Pozar的著名著作《微波工程》中找到一个例子

最后，值得一提的是，调谐双短截线调谐器通常是通过实践中的反复试验来完成的——观看此视频以获取示例。这通常比计算并实现分析解决方案更快。