基于改进的LM算法的可见光定位研究

近年来，随着数据业务和多媒体业务的快速增加，人们对定位与导航的需求日益增大^[1]。面对全球卫星定位系统（GPS）无法在室内获得良好效果的窘境^[2]，Wi-Fi定位^[3]、蓝牙定位^[4]、RFID定位^[5]等一系列以电磁波作为信息媒介的室内定位技术被研究者们相继提出。可见光定位技术作为室内定位技术的一种，在电磁辐射、频谱资源、能量损耗和

安全性等方面具有明显的优势^[6]。因此，针对可见光定位的研究具有现实意义。

目前，已有众多学者分享了在可见光定位领域

的研究成果。文献[7]提出了一种基于自适应混合蛙跳算法的可见光定位方法，虽然启发式算法具有优越的全局搜索能力，但是获得全局收敛解却需要大量计算时间，因此并不适用于嵌入式设备。文献[8]提出了一种基于融合神经网络与指纹的可见光定位算法，虽然算法在仿真条件下能得到极高的精度，但是由于BPNN神经的输入数量是固定的，在复杂的定位条件下算法可能无法灵活的运用冗余光源信息而导致鲁棒性不强。

为解决以上问题，本文提出了一种基于改进的Levenberg-Markuardt算法的可见光定位方法，该系统可以高效的利用有效冗余光源信息，同时以二阶收敛速度获得全局收敛解。其次，针对算法的非负参数的选取进行了研究，证明取合适值时算法迭代次数最少可达17次。此外，研究目前市面常用灯型并推导出不同灯型的VLC信道模型，以期提高可见光定位的适用性。

1  模型研究

1.1 贴片式LED灯的VLC信道模型

不同封装下的LED具有不同的辐照模式^[9]，为了用一种模型来描述多种不同的辐照模式，文献^[10]中F. R. Gfeller等人提出了广义朗伯模型的概念，模型中辐射瓣模式数m作为描述辐射集中程度的一个参量，则在n盏LED下的模型式为

Pr = H(t) ⋅T(β ) ⋅ Ps +n(t) (1)

式中：为加性噪声；为光滤波器增益；而传输函数为可表示为

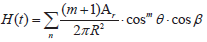 (2)

式中：θ与β如图1所示。

1.2 带反射罩的LED灯的VLC信道模型

灯罩需要被设计为漫反射体^[11]。根据朗伯体的定义，灯罩可以看成一个朗伯型发光体。

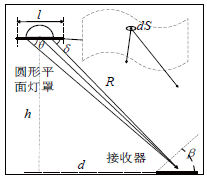
图1 平面反射罩LED灯的辐射场景

假设接收器处于距离LED灯R米远的位置上，接收器的每一个面源dA所接收到的光线如图1所示。基于漫反射灯罩是朗伯体这一前提，面元所感受到的光线亮度为恒定值Le，根据辐射亮度的定义，我们可以得到接收功率微元为

dPr = Le cos β dS d Ω(3)

式中：dS为漫反射罩的发光面元。当R>l时，δ ≈θ且θ为一个常数，而接收面元dA约为接收器面积Ar，根据朗伯体辐射亮度与辐射射出度的关系，将dPr对dS与dΩ进行积分可得

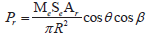(4)

式中：M_e为辐射射出度；S_e为灯罩面积。当漫反射罩为一直径远小于信道距离的平面圆时，该式即为广义朗伯体模型m=1时的情形。

最终得到带平面漫反射罩LED灯的信道传输函数为

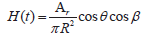 (5)

2   算法设计

2.1总流程图

可见光定位的应用场景一般是大型商场超市、地下停车库、矿道等空旷的场地^[12]。灯作为一种照明设备其布局是紧凑密集的，但通常定位算法只需三盏光源便可确定出具体位置^[13]。为了能够高效的利用这些冗余信息，本文设计了一种基于RSS并采用改进LM算法的可见光定位方法，其基本过程如图2所示。

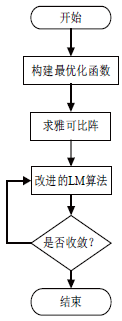
图2 算法流程图

2.2最优化函数与雅可比阵

在忽略反射影响^[14]的条件下，将模型（5）进一步化简可得第n盏LED灯下以坐标向量x为自变量的定位函数为

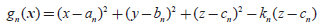(6)

式中：为光源坐标；由光源辐射功率与接收辐射功率的根号比确定。同时将n个定位函数改写成无约束优化函数形式为

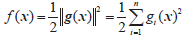
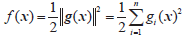 (7)

其雅可比阵Jk定义为

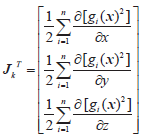 (8)

由上述过程可以看出，函数形式与其雅可比阵能根据光源信息多少进行增减，因此算法可灵活地运用有效冗余信息进行定位。当n>3时算法可收敛于确定解,且当n越大时收敛解的准确度越高^[15]。

2.3 改进的LM定位算法

改进的LM算法通过引进非负参数，克服了目标函数的雅可比阵几乎奇异或坏条件时牛顿步所带来的困难^[16]。同时，为了避免陷入局部极小值，使算法获得全局收敛解，引入信赖域半径对非负参数进行修正。

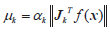(9)

式中：二范数部分为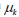的更新规则，不同的更新规则对于算法的收敛性能影响很大。而算法将以如下规则迭代。

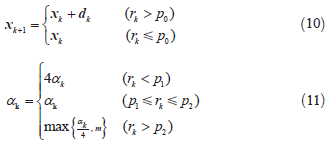
式中，dk表示目标向量x一个搜索方向为

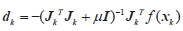  (12)

更新准则rk为实际下降量于模型下降量之比为

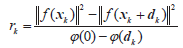(13)

式中：模型ϕ (d )定义为。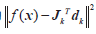

3 实验与结果分析

在1.48m x 1.51m x 1.65m的空间中搭建定位环境，四盏3W白光LED灯泡分别安装在四个上顶点处并分别以200Hz、300Hz、400Hz、500Hz的频率闪烁，而产生的混频光信号利用OPT101进行光电转换，模数转换后在STM32F407平台进行测试实验。

3.1 算法测试

为了探究选取何种形式时，LM算法对式（7）的解算性能最佳，将STM32F407获取的五个定位点数据并传回PC端，在Matlab环境下进行LM算法的解算过程。实验时记录算法迭代次数，并以此作为判断准则。

参数方面，取m、、分别为1e-6、1e-4、0.25、0.75，设置最大迭代次数为100，终止条件为<1e-5，其中，初始向量x中z轴坐标应尽可能大于真实高度。

表1 LM算法迭代次数

表2 改进的LM算法迭代次数

由表1与表2可以看出，LM算法迭代所用次数基本超过100次，而改进的LM算法则在有限次数内满足迭代退出条件。

结果表明，LM算法对于定位方程的解算陷入局部极小值而无法跳出循环，而改进的LM算法则可以获得满足精度条件的全局极小值。同时，改进的LM算法的非负参数 取 时，收敛所用的迭代次数最小。

3.2 定位测试

在定位空间中，分别在三种不同的高度(1.65m、1.55m、1.45m)下进行定点测量，如图3所示。

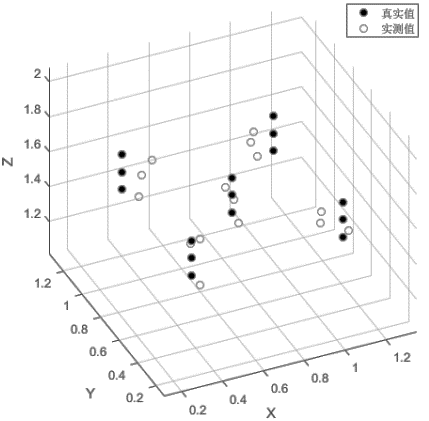
图3 数据分布图

结果表明，系统的定位误差(RMSE)为12.4cm，考虑到测量系统存在偏差，该值的置信区间约为15cm至10cm。

4   总结

本文提出基于改进LM算法的可见光定位方法相比于神经网络，理论上拥有更好的灵活性与鲁棒性，而相比于启发式算法，实际中选取最优更新规则时算法最快只需要17步的迭代便可以收敛到全局最优解，因此更加适合应用于嵌入式设备。

但相比于仿真结果，真实环境下所得到的RMSE有所增大，这说明模型并非完美，而能让可见光定位模型适应更复杂多变的实际环境，应是继续研究的重点。

参考文献：

[1]  高燕龙, 施安存, 张运方, 等. 基于白光LED的室内高精度定位算法的实现[J]. 半导体光电, 2015,36(01):141-144.

[2]  姜西瑞. 基于GPS和GSM/GPRS的定位系统的设计与实现[D]. 中国科学院研究生院（计算技术研究所）, 2006.

[3]  He X, Badiei S, Aloi D, et al. WiFi iLocate: WiFi based indoor localization for smartphone: 2014 Wireless Telecommunications Symposium, 2014[C].

[4]..Schuermann V, Mann T, Buda A, et al. Integrating bluetooth localization into existing TCP/IP networks: 2009 IEEE International Workshop on Intelligent Data Acquisition and Advanced Computing Systems: Technology and Applications, 2009[C].

[5]  Ahmad M Y, Mohan A S. RFID reader localization using passive RFID tags: 2009 Asia Pacific Microwave Con- ference 2009 [C].

[6]  董文杰, 王旭东, 吴楠, 等. 基于LED光强的室内可见光定位系统的实现[J]. 光通信技术, 2017,41(03): 12-15.

[7]  陈爽, 金嘉诚, 张月霞. 基于可见光的自适应混合蛙跳定位算法[J]. 半导体光电, 2018,39(06):858-862.

[8]  刘冲, 张月霞. 融合神经网络和指纹的可见光定位算法研究[J]. 半导体光电, 2019,40(06):891-895.

[9]  谭家杰, 邹常青. 室内多环LED的信道特性分析[J]. 系统仿真学报, 2013,25(12):2906-2911.

[10].Gfeller F R, Bapst U. Wireless in-house data com- munication via diffuse infrared radiation[J]. Proceedings of the IEEE, 1979,67; 67(11; 11):1474-1486.

[11] 张志新, 徐洪振, 谢凤军, 等. 高校新型照明灯具节能技术应用研究[J]. 昆明理工大学学报(自然科学版), 2017,42(05):65-73.

[12] 江运力. 基于RSSI及图像传感器室内可见光定位系统研究[D]. 南京邮电大学, 2014.

[13] 陆霞. WiFi定位技术——基于质心定位的三边定位算法的研究[J]. 电脑知识与技术, 2013,9(25):5765-5767.

[14] 张秀楠, 邵建华, 柯炜, 等. 反射与噪声对室内可见光定位系统精度影响及其克拉美罗界[J]. 南京师大学报(自然科学版), 2017,40(03):102-109.

[15] 胡海婧. 考虑误差抑制的室内三维定位算法研究[D]. 哈尔滨工程大学, 2017.

[16] 杨柳, 陈艳萍. 求解非线性方程组的一种新的全局收敛的Levenberg-Marquardt算法[J]. 计算数学, 2008(04): 388-396.