基于矩阵乘法器的MP3音频解码系统的优化设计
0 引言
MP3(MPEG Audio Layer 3)是一种以高保真为前提实现的高效压缩技术。MP3音频编码器复杂,压缩率很高,但其音色和音质还可以保持基本完整,因此该音频格式文件在计算机、网络和各种电子设备上都得到了广泛运用。
由于MP3音频解码相对比较复杂,为了达到在控制成本的范围内实现快速解码的要求,提出了在SoC上通过增加矩阵乘法器运行快速的两个16点DCT算法,进一步提高MP3解码速度的可行性方案。
1 MP3解码流程分析
MP3解码的流程如图1所示,解码的主要过程包括同步处理、解帧头、解边带信息、解比例因子、Huffman解码、逆量化、频率线重排序、立体声处理、混叠重建、改进离散余弦逆变换(IMDCT)、频率倒置处理、子代综合滤波,最后输出原始的PCM数据。
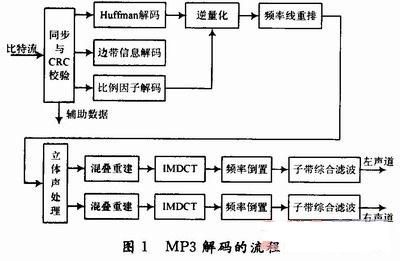
在这些过程中由于IMDCT和子带综合滤波的算法比较复杂,占用硬件资源较多,处理时间长,因此功耗所占比例相应较高。表1是在DSP平台上成功移植后,对代码进行耗时分析的结果。
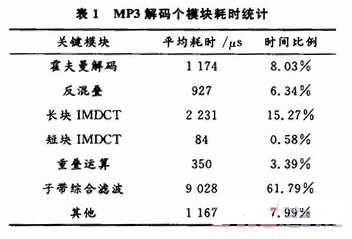
根据表1可知,子带综合滤波占了整个解码时间的60 %以上,是决定解码速度的最关键模块;其次是长块IMDCT运算,占了整个解码时间的10%以上。若采用MPEG-1建议的算法流程,数值计算主要集中在子带综合滤波上。以两声道48 kHz采样率为例,乘法运算量为(48 000/32)×(64×32+512)×2=7 680 000次/s。因此,子带综合滤波是MP3解码器的优化重点,减少子带综合滤波的计算量和计算时间是MP3解码器实现的核心。
2 子带综合滤波分析
子带综合滤波是MP3解码的最后一部分,也是解码过程中最为耗时的关键步骤。它负责从IMDCT的输出值中把PCM值还原出来,可以分成5个步骤。首先是Matrixing(矩阵)运算,即,2,…,63。由公式可知,它从32个子带Sk的每个子带中取出一个值组成32个值送入一个矩阵中进行运算,然后把输出Vi的64个结果放入一个1 024的先入先出(FIFO)缓存中,再从1 024值中取出一半,组成一个512矢量Ui,并对这512矢量进行加窗运算,即Wi=UiDi,i=1,2,…,511,加窗系数Di由MP3官方协议 AnnexB Table3-B.3提供。最后将加窗结果Wi进行叠加生成32个时域PCM输出。
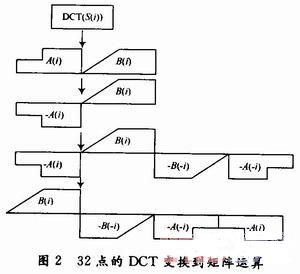
1次矩阵运算乘法和加法运算过程分别为1 024次和992次,完成1个声道的解码需要18次矩阵运算。矩阵运算是子带综合滤波的关键步骤。实际上,Konstantinos Konstantinides提出的方法,只需要做一些变化就可以通过32点DCT变换成矩阵运算。
2.1 32点快速DCT算法分析
快速DCT变换算法主要基于系数矩阵分裂方法,增加输入的预处理,使得乘法和加法计算量减半。32点的DCT变换到矩阵运算如图2所示。其中V(1×64)表示矩阵的输出,A,B都是长度为1×16的矢量,(A,B)表示32点DCT的输出。
由于32点的DCT可以分解成2个16点的DCT变换,依次类推可以分解成8点的DCT变换,考虑到定点数字信号处理中的有限字长效应,实际只需分解1 次,将32点DCT化成2个16点的DCT。简化子带滤波流程以及使用快速DCT变换后,子带综合滤波部分的运算量可以减少约60 %。
由32点DCT分解为2个16点DCT过程推导如下:
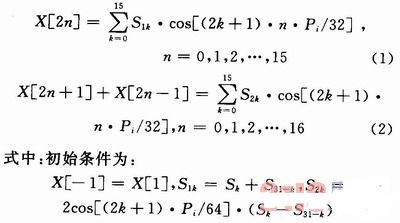
2.2 基于矩阵乘法器的快速DCT算法优化
3×3矩阵乘法器由触发器和乘累加器组成,是高性能DSP处理器的重要部件,也是实时处理的核心,其速度直接影响DSP处理器的速度。矩阵乘法器的实现有很多种,基本上都基于并行计算原则。由于每列结果与其他列不相关,因此可以通过增加乘法器多列同时计算,经过n次乘累加就可以得到最后结果。图3给出矩阵乘法器的结构。
显然,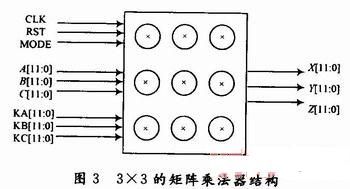 这种结构的计算速度很快,但是使用乘法器会因矩阵维数n的增加而快速增加,使用的触发器也很多。在很多场合下,只要满足处理速度的要求,完全没有必要浪费这么多硬件资源,而是只要1个乘累加单元流水作业,分步计算每1列结果既可。在做乘累加计算1个元素时候,准备下一组参与运算的数据,如此循环,同样可以获得较高的处理速度。
这种结构的计算速度很快,但是使用乘法器会因矩阵维数n的增加而快速增加,使用的触发器也很多。在很多场合下,只要满足处理速度的要求,完全没有必要浪费这么多硬件资源,而是只要1个乘累加单元流水作业,分步计算每1列结果既可。在做乘累加计算1个元素时候,准备下一组参与运算的数据,如此循环,同样可以获得较高的处理速度。
在该设计中,由于B矩阵是1×n的一维向量输入数据,A矩阵为DCT系数矩阵,A矩阵中的元素为n个系数的线性组合,因此整个矩阵乘法器需要2组n个触发器分别存放输入数据和n个系数,1个乘累加单元。输入数据X[0:n],从X[O]到X[n]循环n次进入乘法器,使用选择信号Assi-gn[0:n] 选择系数C[0:n],另外系数符号由Sign信号软件控制,基本结构如图4所示。
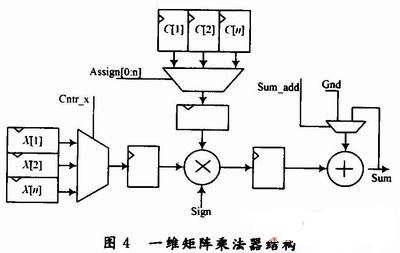
由于DCT计算本质上就是n×n矩阵乘法运算,而n×n矩阵乘法器是在通用乘法器的基础上增加2组分别存放系数矩阵的系数C(n)和输入X(n)的n个寄存器,使之实现长度为n的乘累加功能,同时还需保存上次乘法结果。其中,DCT中的系数是一组n维基的n种线性组合。只需1次输入n个系数,使用软件进行选择和符号控制就可实现这些不同系数组合,无需反复往寄存器中置数,大大提高了取数/置数的效率,节省了整个DCT的运算时间。
因此在计算32点的DCT,可将32点DCT分解为2个16点的DCT计算,计算量也减少1倍。可以使用2组16×16的矩阵乘法器并行计算,使得计算时间大幅减少。表2是通过增加矩阵乘法器优化处理后,子带综合滤波使用不同实现方式所需要的时间。
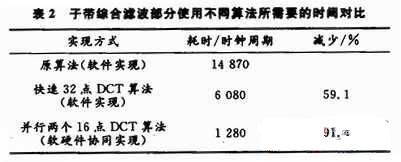
结果表明,第2.1节中使用快速32点DCT算法改进子带综合滤波计算是有效的,直接减少59%的计算时间。在采用并行2个16×16矩阵乘法器加速快速 32点DCT的计算,可以取得明显的效果:使得计算时间比原算法减少了约91.4%,而且硬件上只增加1个乘法器和30个数据锁存器,以及部分控制电路。使用软硬件协同操作就可以获得子带综合滤波计算速度上的大幅度上升。
3 结语
该设计面向SoC实现了利用增加矩阵乘法器就可加快基于32点快速DCT算法的MP3解码中子带综合滤波的处理速度,大大缓解了系统的颈瓶,使得采用系统主频比较低(fs≤100 MHz)的SoC平台进行MP3的解码成为可能。








评论