轮毂盘式无铁心永磁同步电机永磁体结构优化

作者 刘福贵 王彦刚 赵振兴 刘慧敏 高春兰  河北工业大学电磁场与电器可靠性省部共建重点实验室(天津 300130)

*基金项目：天津市自然科学基金(编号：15JCYBJC16400)

刘福贵(1972-)，男，博士，教授，研究方向：电磁场与磁技术。

摘要：从优化永磁体结构的角度出发，提出将不等厚排列技术与90°Halbach阵列相结合方法对磁钢的排列结构分析，通过改变磁钢排列结构以进一步提高盘式无铁心永磁同步电机(以下简称为DCPMSM)气隙磁密的基波幅值及波形的正弦性，达到提高电机性能的目的。本文通过有限元仿真软件对16极盘式永磁同步电机进行建模，分别选取不等厚排列电机模型、不等宽90°Halbach排列电机模型和改进型90°Halbach排列电机模型进行静态气隙磁场分析对比。仿真数据表明，“不等厚排列技术+90°Halbach阵列”使得周向磁密波形和切向磁密波形都大为改善，磁场波形更接近于正弦分布特征，其中周向磁密波形畸变率(THD)Bmin可降低到1.35%，气隙周向磁密幅值Bδav提高到0.5465T。

引言

　　针对车用永磁同步电机高效率、高功率密度的要求，气隙磁场的波形须为正弦波，幅值应足够高，以电机磁场为优化目标进行分析^[1]。为确定电机磁场的优化变量，本文对其磁路进行定性分析，得到了影响磁场的主要因素是永磁体材料以及结构尺寸。因此，磁钢尺寸成为磁场优化的关键。将不等厚原理应用于90°Halbach结构，能够兼顾气隙磁场的幅值与波形，对于提高电机功率密度、降低转矩脉动^[2]等具有重要意义。并且利用盘式电机的设计原则对该特种电机的主要电磁参数进行了推导，对轴向磁场电机的后续设计提供了理论依据。

　　针对永磁同步电机对气隙磁场^[3]的要求，提高电机的效率，降低电机的转矩脉动^[4]及振动噪声，电机磁场波形要接近正弦分布特性。为了兼顾以上要求，可以从电机永磁材料、磁钢形状和排列方式等方面考虑。永磁体选用磁性能优异的钕铁硼材料。而对于磁钢结构的研究，有文献提出根据气隙磁密波形设计不等厚磁钢^[5-6]和采用不等厚磁钢排列削弱气隙磁密的谐波分量^[7]，但有很少文献理论地介绍轴向充磁磁钢的不等厚排列原理。有学者通过比较研究不同角度的Halbach阵列^[8]，得到最优的排列方式。90°Halbach阵列充磁较其他角度的方便^[9]、结构排列简单、对工艺要求低^[10]，虽能够满足电机对气隙磁密幅值的要求^[11]，但波形正弦性不够理想。因此，提出将不等厚排列技术与90°Halbach阵列相结合方法对磁钢的排列结构^[12]进行设计。

1 电机电磁参数与气隙磁密的分析

　　气隙磁密的基波幅值提高以及波形的正弦性对电机的各性能参数具有很重要的意义。当保持电机的主要尺寸不变时，通过对磁钢的优化，提高电机气隙磁密的基波幅值，使得电机的电磁转矩和电磁功率得到提高;波形的正弦性对电机的空载反电动势和转矩脉动有很紧密的关系^[13]。

　　根据电机电磁参数与气隙磁密的关系，气隙磁密的基波幅值与电机的空载电动势、电磁转矩和电磁功率有紧密的关系。针对改善DCPMSM每极下的平均气隙磁密的幅值和波形，目前有很多专家学者对电机的永磁体结构进行研究，其中，90°Halbach阵列技术和不等厚排列得到了很广泛的应用，并且两者相较普通磁钢排列，平均气隙磁密的幅值得到提高，正弦性也有显著改善。因此，本文针对气隙磁密的幅值及波形的正弦性，对电机的不等厚排列模型和不等宽90°Halbach阵列模型进行磁场仿真。

2 两个电机模型的磁场仿真

2.1 不等厚排列电机模型的磁场仿真

　　每极有五块不同厚度的磁钢组成，中间磁钢厚度由hm1表示，紧邻的里侧两块磁钢厚度为hm2，最外侧两块磁钢厚度是hm3，且满足h_m1>h_m2>h_m3。改变三块磁钢的厚度比可以得到幅值、波形均不同的气隙磁场。

　　仿真结果显示，改变h_m1时，B_δav与(THD)_B随h_m2、h_m3的变化规律同h_m1=15mm的情况：每一个h_m1取值都有对应的(THD)_Bmin;B_δav随h_m2减小同样呈减小趋势，即主要受hm₂影响。

　　由于受尺寸限制，hm₁=12mm对应的6.61%并不是(THD)B的极小值，而是仿真所取到的最小值，但并不影响最终结论。可见，随hm₁的单调变化，(THD)_Bmin同样先减后增，故存在最优情况，取(THD)_B值为1.70%，此时，B_δav=0.4615T，(hm₃,hm₂,hm₁)=(2,9,18)。

2.2 不等宽90°Halbach排列电机模型的磁场仿真

　　每极轴向充磁磁钢与切向充磁磁钢所占的几何角度比值用k表示。不等宽与不等厚原理相同，都是改变磁钢的磁化方向长度;前者针对切向充磁磁钢，后者针对轴向充磁磁钢。

　　波形幅值随比值k的减小而增大，波形由马鞍形波向尖顶波方向发展。减小比值k相当于增大切向充磁磁钢的宽度，由仿真结果易知，增大切向充磁磁钢所占的比例有利于增大磁密幅值，但波形质量也会变差;而增大k值，则相当于增大轴向充磁磁钢的宽度，其极限情况即对应普通的N、S排列结构，因此波形会向马鞍状发展。因此，简单地改变90°Halbach结构一极的宽度比，无法得到理想的效果。

3 改进型90°Halbach排列的电机模型磁场仿真

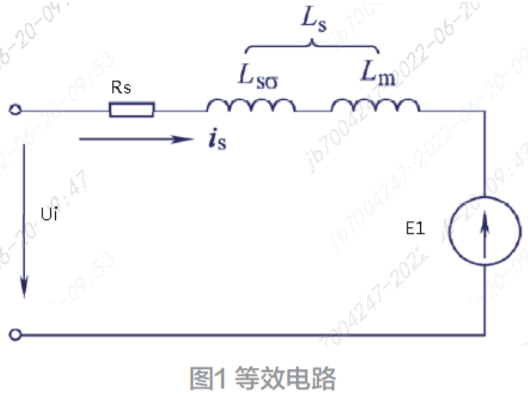
　　将轴向不等厚排列应用于90°Halbach阵列每极的两块磁钢，其磁钢平均半径处的切向展开示意图如图1所示。即原有的每块磁钢变成三块不同轴向厚度的磁钢，中间厚度取为h1，对应的几何角度所占比例为div1;两边厚度为h2，所占的比例均为div2。

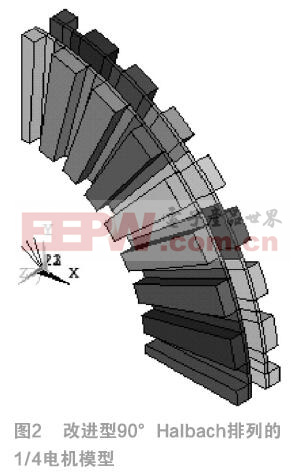
　　电机的四分之一仿真模型如图2所示，是k取1前提下拥有最佳周向磁密波形的模型。该模型中，h₁=12mm，h₂=2.4mm，div₁=3.5/6。

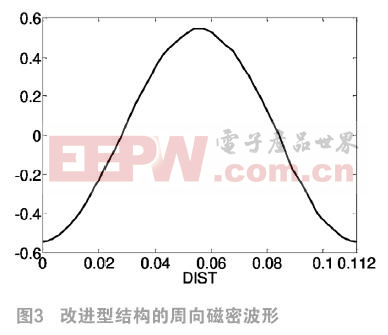
　　图3显示的是改进型电机的周向磁密波形，幅值为B_δav=0.5465T，且波形非常接近正弦波。与45°Halbach排列等结构相比，该模型虽然每极磁块数增多，但在充磁方面仍然占优势，且磁密波形也能达到要求。图4所示的径向磁密波形，相较90°Halbach基础结构更加接近平顶波，永磁体内外径间的磁场变化比较稳定。

　　令r=div₁/(2*div₂)，表示中间磁钢与两边磁钢所占几何角的比值。具体优化过程：

　　(1)k=1。对于改进型的等宽结构，比较r变化时气隙磁场的变化情况。首先对r=1时的电机模型进行仿真，此时div₁=2*div₂。改变h₁、h₂，分析气隙周向、径向磁场变化情况。

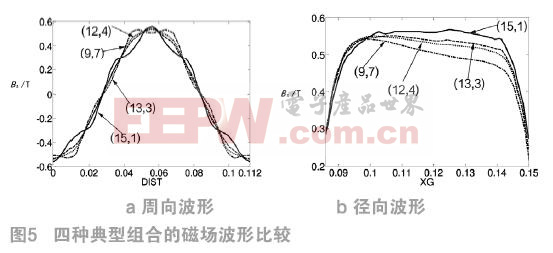
　　仿真结果表明，B_δav随中间磁钢的厚度h1的增大呈上升趋势，(THD)_B则变化为先减小后增大，并在(h₁,h₂)取厚度组合(13,3)时获得最小值;由周向波的变化趋势就不难推断波形质量最佳的情况必位于这组数据的中间某个组合;径向波形以组合(12,4)为斜顶波与准平顶波的分水岭，故(13,3)组合的径向波形位于准平顶波之列。综合分析，(13,3)是r=1时的最佳厚度组合。图5比较了(h₁,h₂)取四种典型值的磁场波形。

　　对于r≠1的情况，取比值5:1~1:5之间的8种改进型结构模型进行仿真。结果显示，(THD)_B及周、径向波形随组合(h₁,h₂)的变化规律基本同r=1情况：周、径向波形变化趋势大体一致;而对于某一特定的r值，对应的(THD)_B随h₁增大的变化满足先减小后增大的规律，(THD)B存在局部最优解(极小值)。但当r取5:1、4.5:1.5、1.5:4.5、1:5四种偏离1:1较远的值时，在实际合理尺寸范围内，(THD)_B并不存在极小值，处于发散状态，且对准全局最优解(k=1时)不构成影响。

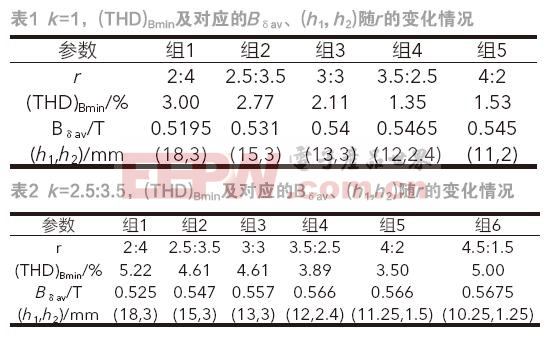
　　综合比较r取不同值的(THD)_B极小值变化情况，结果总结列入表1。其中(THD)_Bmin表示周向磁密波形的THD极小值。(THD)Bmin随r的增大先减小后增大，故k=1时，(THD)_B的准全局最优解存在，为1.35%，此时r=3.5:2.5，对应的(h₁,h₂)取(12,2.4)，B_δav为0.5465T。

　　(2)k≠1。对于改进型的不等宽结构，同样令k取5:1~1:5之间的8个比值，仿真过程同上。对于k=2.5:3.5情况，仿真结果如表2所示。据前所述，最后一组数据并非仿真的最佳结果，而是考虑到实际尺寸限制所取的最小值。与表1比较，k取2.5:3.5时，r值对应的(THD)Bmin总体增大，但随r的变化规律却相同，且相应的厚度组合(h₁,h₂)也基本吻合。故k=2.5:3.5时，(THD)_B的准全局最优解存在，为3.50%，B_δav为0.566T。

　　由于k取其他七个比值时，周向磁场的仿真波形畸变率较严重，(THD)B的准全局最优解的情况更糟。对于其中任一种取值，r值所对应的(THD)B要么存在极值，但要明显高于前述的两种情况，要么发散、不存在极值。

4 结论

　　通过对90°Halbach结构^[14]的仿真，增加轴向充磁磁钢的轴向厚度、将轴向充磁磁钢划分成不同厚度的若干块小磁钢或是增加切向充磁磁钢所占的几何角度等简单地结合不等厚设计的诸多方法都无法得到高质量的波形。因此考虑对一对极的两种充磁磁钢都运用不等厚设计，将单块的每种充磁磁钢用三块不等厚磁钢代替。这样虽然增加了每极磁钢块数，但周向磁密波形和切向磁密波形都大为改善，结果验证了不等厚排列应用于90°Halbach结构的合理性，通过仿真数据显示，(THD)B的最小值为1.35%，对应的k=1，r=3.5:2.5，(h1,h2)=(12,2.4)，Bδav为0.5465T。综合考虑电机的实际情况，改进型90°Halbach电机采用周向磁密波形畸变率最小所对应的磁钢结构，相对于90°Halbach型和不等厚型电机在气隙磁密基波幅值和波形正弦性上都有所改善。

　　参考文献：

[1]Nair S S,Nalakath S,Dhinagar S J.Design and analysis of axial flux permanent magnet BLDC motor for automotive applications[C].IEEE International Electric Machines & Drives Conference，2011:1615-1618.

　　[2]Aydin M, Gulec M.Reduction of Cogging Torque in Double-Rotor Axial-Flux Permanent-Magnet Disk Motors: A Review of Cost-Effective Magnet-Skewing Techniques With Experimental Verification[J].IEEE Transactions on Industrial Electronics，2014,61(9): 5025-5034.

　　[3]Li J G,Wu D Y,Zhang X D.A new permanent-magnet vernier in-wheel motor for electic vehicles [C].Proceedings of IEEE Vehicle Power and Propulsion Conference，2010.

　　[4]Huang C C,Li P L,Chuang F C,et al.Optimization for Reduction of Torque Ripple in an Axial Flux Permanent Magnet Machine[J].IEEE Transactions on Magnetics，2009,45(3):1760-1763.

　　[5]方淑丹.永磁直流电动机不等厚瓦形磁钢的设计[J].微特电机,1999(1):15-18.

　　[6]刘超,孙立志,孙立.永磁同步伺服电动机气隙磁场优化设计[J].微电机,2010,43(11):24-26.

　　[7]金友华,王宏伟.基于Ansoft优化永磁同步电机气隙磁密[J].微电机，2013,46(12)：24-26.

　　[8]孙程英.不同结构永磁同步电机的磁场分析[D].北京:华北电力大学,2008.

　　[9]闫杰.盘式无铁心永磁同步电机磁场分析及磁钢结构优化[D].天津:天津大学,2004.

　　[10]Bumby J R,Martin R.Axial-flux permanent-magnetair-cored generator for small-scale wind turbines[J].Proc.IEEE Proceedings-Electric Power Applicatio-ns，2005,152(5):1065-1075.

　　[11]李桂丹,于海峰,王晓远,等.基于Halbach阵列的盘式无铁心永磁同步电机磁钢优化[J].微电机,2015,48(2):1-6.

　　[12]谢龙汉,耿煜,邱婉.ANSYS电磁场分析[M].北京:电子工业出版社,2012.

　　[13] Giulii Capponi F,De Donato G,Caricchi F.Recent Advances in Axial-Flux Permanent-Magnet Machine Technology[J].IEEE Transactions on Industry Applications，2012,48(6):2190-2205.

　　本文来源于《电子产品世界》2017年第4期第33页，欢迎您写论文时引用，并注明出处。