反射式RAP型椭圆偏振光谱仪及其应用

因此，只要测出材料的光学常数 n 和 k，即可换算得到其 ε～，或知道ε～即可求出材料的其他光学常数。

椭偏光谱测量以光的偏振态为测量手段，可快速、准确地获得材料的光学常数与复介电函数，并且能方便、快捷地应用于薄膜材料的测量，是研究薄膜材料物理性质的理想手段［4］。

另外，Kramas 等的研究表明:由因果关系决定的光学响应函数 ε～的实部与虚部之间，光学常数 n 与 k之间并非完全独立，而是由一系列表达式所联系，即Kramas-Kronig 关系( 简称为 K-K 关系):

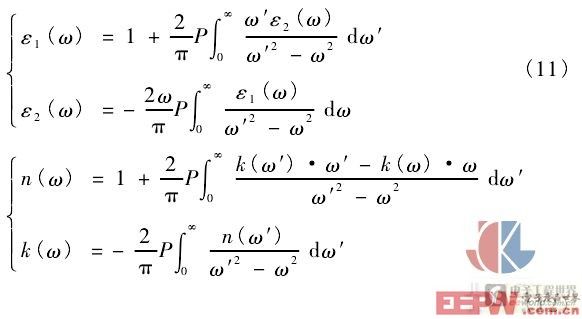
式中，光频率积分范围为从 0 到无穷大，即全光谱。只要获得以上 n～和ε～4 个量中任何 1 个，即可通过 K-K关系求出其余 3 个。然而，由于绝大多数光源的光谱范围非常有限，无法获得 n～和ε～4 个量中任何 1 个的全光谱数值，从而给全光谱积分求值带来困难，若要对测量光谱区以外的数值进行外推，则会引入巨大的误差，这是使用 K-K 关系的局限性。

2. 2 菲涅尔公式和椭偏参数的推导［1，3］

光在传播过程中遇到 2 种不同介质的分界面将会发生反射和折射，在界面两侧光的相位相同，并且 E和 H 必须满足边界条件。如图 1 所示，z = 0 两侧为无穷大各向同性均匀介质，其复折射率分别为 n～1和 n～2，考虑一单色平面波入射在界面发生反射与折射的情况。在分界面处光的相位相同，可得到入射角和反射角、折射角的关系:

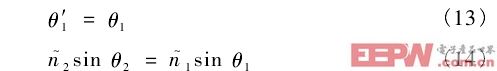
图 1 光在 2 种不同介质分界面处的反射与折射把入射光分为偏振方向平行于入射面的 p 光和偏振方向垂直于入射面的 s 光，p、s 光分别反射与折射，其相位与强度独立变化，在分界面处 E 和 H 满足边界条件，由此可得 p、s 光各自反射系数 r～与透射系数 t～:

以上即为菲涅尔公式。

椭偏光谱测量的原理基于 p、s 光在介质界面处相对独立的反射与折射规律，对于反射式测量的椭偏光谱仪，定义椭偏参数Ψ和 Δ，其满足

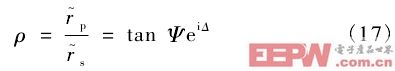
椭偏仪测量的是 p、s 光反射系数的比值，tan Ψ 表示两者反射系数幅值之比;Δ表示两者反射后相位的移动，这 2 个量可通过相位调制，旋转起偏器或检偏器的方法测量。对于体材料，可用环境介质 /样品两相模型进行分析，当入射角为θ0时，将式(15)代入(17)可得

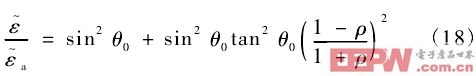
表示与被测材料界面接触的环境介质的复介电函数，在通常的测量环境中环境介质为空气，所以ε～a= 1。由此可见，椭偏光谱测量无需通过 K-K 关系进行计算而能够直接获得材料的介电函数，从而获得相应的光学常数，克服了运用 K-K 关系的局限性。

3 反射式 RAP 型椭偏光谱仪

椭偏仪最初采用消光式的测量方法，即通过寻找光强输出最小的位置为测量手段，但相位补偿器的引入以及光强极小值位置的判断容易引入误差，测量精度不高［1］

1975 年，Aspnes 首次成功设计了光度式椭偏仪［2］，这种椭偏仪不需要相位补偿器，只需旋转检偏器并记录反射光光强随检偏器转动角度变化的规律，通过计算机即可计算出反射光的偏振状态。光度式椭偏仪不需要相位调制，并且免去了光强极值判断，因此可获得很高的测量精度，本文采用的是反射式同时旋转检偏器与起偏器(Rotating Analyzer and Polariz-er，RAP)的光度式椭偏仪［8-10］。

根据式(18)，对于环境介质 /样品两相结构，在环境介质介电函数已知的前提下只要测量获得椭偏参数Ψ 和 Δ 即可通过计算获得样品的光学常数，图 2 为实验所用反射式 RAP 型椭偏仪的实验装置示意图。P0、P 和 A 均是偏振器件，其中 P0为固定起偏器，其偏振方向为 S;P 和 A 分别为可转动的起偏器与检偏器，两者的初始偏振方向为 S，测量时 P 与 A 同时转动，A 的转速是 P 的 2 倍。探测光的入射角 θ 在大于 35°范围内可调，转动精度优于 0. 01°，椭偏仪的测量过程均由计算机自动控制，数据的采集与初步计算通过计算机完成。该仪器采用波长为 650 nm 的半导体激光器作为单色光源，探测器采用光电倍增管，其信号大小由A / D 卡采集。 整个系统的运行由一台工业计算机控制，系统被置于光学隔振平台上，以保持系统的稳定、可靠与高精度运行。

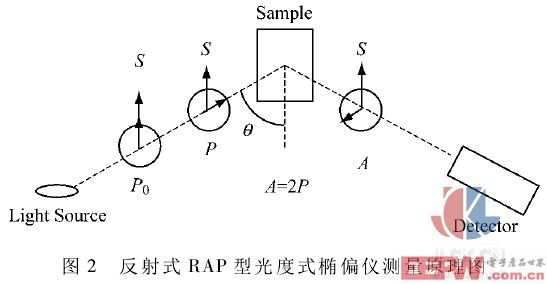
根据图 2 可得，进入探测器的反射光电场强度为