FFT的前世今生

请看下面的实例：

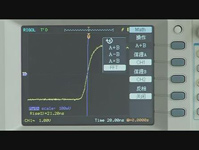
图1中正弦波测试使用的时基是5ns/div，波形时间长度是50ns，计算FFT之后的频谱分辨率是20MHz(1/50ns)，

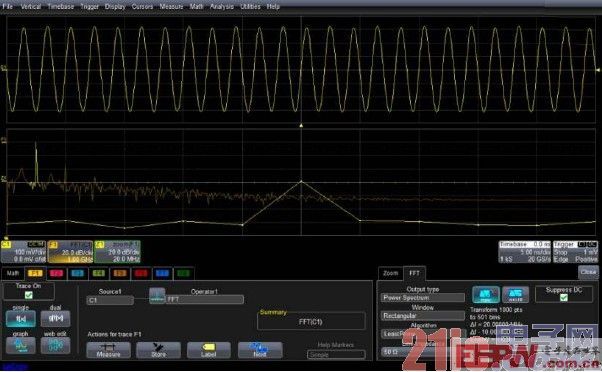
图1 捕获50ns的信号，频率分辨率是20MHz

如果改变时基设置，频谱分辨率会有变化。如图2所示：将时基设置为10ns/div，波形长度是100ns，频谱分辨率可以提高到10MHz。

对于通过补零的方法增加FFT频谱的视在分辨率，力科的示波器也有相应的解决方案。力科示波器使用了两种非常常用的FFT算法供用户选择：Cooley-Tukey算法和LeastPrime算法。Cooley-Tukey算法也称为Power2算法，它提供了计算机一种非常快速的FFT计算方式，计算的FFT点数规模是2的整数方次，因此它会在示波器时域采集的信号中截取2的N次方的整数来作为FFT计算的时域样本，该截取的整数是最接近于采样点的整数。如下图2所示：

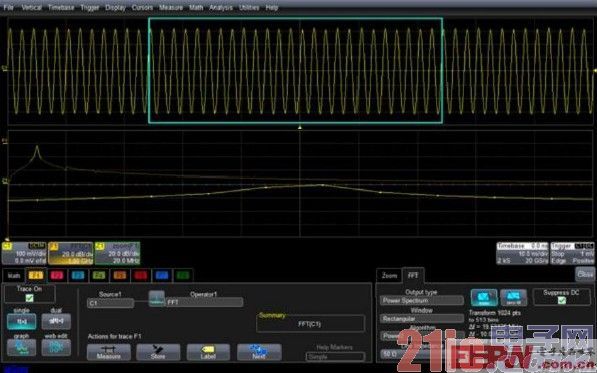
图2 捕获100ns的信号，频率分辨率是10MHz

图中的正弦波频率为500MHz，时基设置为10ns/div，采样率为20GS/s，时域采样点数为2000points，使用Power2算法截取2000点中的1024点(210)，如图中的蓝框所示(注意是从信号的中间部分截取)，因此截取的时间窗口为1024×20ps=51.2ns，是500MHz信号的25.6个周期，由于截取的周期非整数倍，不可避免会产生频谱泄露，如图中FFT的旁瓣所示，此时的频率分辨率可以达到19.35125MHz。

如果采用另外一种FFT算法LeastPrime，可以将整个示波器时域采集的采样点进行FFT运算，LeastPrime算法计算的FFT点数规模是2N+5K，因此2000点=24+53，不需要截取原始数据就可以运算，但是代价是计算的速度可能会慢一些(尽管我们可能觉察不到)，频率分辨率可以提高到10MHz。

使用Power2算法也可以不采用截取原始波形的方式，此时我们可以选择Zero Fill(补零)的方式，增加采样点数。比如，在2000点中补48个点，2048=211，如图3所示：

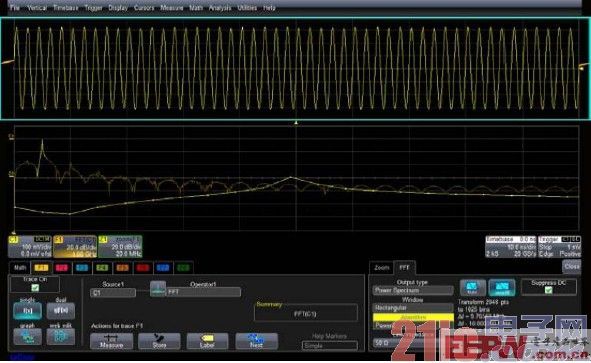
图3 补零的放出提高频率分辨率