基于上游渐扩管安装条件的内锥流量计性能预测

图2 内锥流量计三维模型及网格剖分(局部)
2.2 湍流模型与边界条件
对比目前常见的湍流模型,标准k-ε模型在科学研究及工程领域获得了最广泛的检验与成功应用,但当应用于强旋流、弯曲壁面流动或弯曲流线流动时,会产生一定的失真。杨胜等在对汽车外部流场仿真研究中,比较了spalart-Allmaras-方程模型、标准k-ε模型、RNG k-ε模型、Realizable k-ε模型和RsM模型的预测结果后,认为RNG k-ε模型的预测性能要强于其余的4种模型。因此研究中采用RNG k-ε模型计算流场,利用有限体积法实现控制方程的离散化,采用sIMPLE算法进行求解。根据GAN等的研究,在仿真时,除压力项采用二阶迎风格式外,其余都利用了QuiCk格式进行离散。亚松弛因子采用FLUENT软件的默认值,实践证明其收敛效果比较好,残差收敛精度设为10-5。计算时选取5个流速点,方向取入口面的法线方向。其中100MM口径内锥流量计仿真湍流参数如表2所示。
表2 100MM口径内锥流量计仿真湍流参数 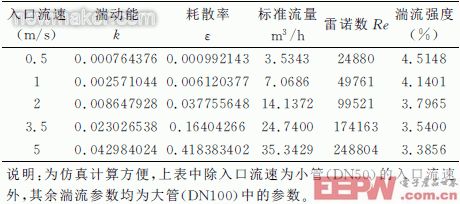
(1)湍动能k求解

湍流强度依据经验公式进行计算

(2)湍流耗散率ε的求解

2.3 计算结果
流出系数C是内锥流量计的关键参数之一,对于不可压缩流体,流出系数C定义为內锥流量计中实际流量与理论流量的比值。根据能量守恒定律和质量守恒定律,可以推导出C的计算公式为

通过点表面积分法,对数值仿真计算结果进行后处理,计算锥体上下游的压力差,并根据公式(4)计算出流出系数。图3即为3种β值在上游渐扩管安装条件下流出系数与雷诺数的关系曲线。
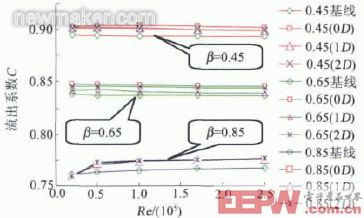
图3 C-Re曲线
2.4 压力场分析
以β=0.45,入口流速υ=0.2M/s为例,提取锥体上游和下游局部压力场云图,分析上游不同直管段长度对上、下游压差的影响。压力场云图如图4~6所示。



评论